Magari algebra

diagonalizable algebra

A Boolean algebra enriched with a unary operation $\vartriangle$. In the so-expanded signature, the Magari algebra is defined by the axioms of Boolean algebra and the following three specific axioms:

1) $\vartriangle 1 = 1 $;

2) $\vartriangle ( x \wedge y ) = \vartriangle x \wedge \vartriangle y $;

3) $\vartriangle ( C \vartriangle x \lor x ) = \vartriangle x $.

Here, $ C $ denotes complementation and the unit $ 1 $ is the greatest element of the Magari algebra with respect to the relation $ \leq $. The notation $ \pmb\tau $ is often employed instead of $\vartriangle$.

One sometimes regards the Magari algebra with the dual operation $ \pmb\sigma $( $ \pmb\sigma = C \vartriangle C $), defined by the axioms:

1') $ \pmb\sigma 0 = 0 $;

2') $ \pmb\sigma ( x \lor y ) = \pmb\sigma x \lor \pmb\sigma y $;

3') $ \pmb\sigma ( x \wedge C \pmb\sigma x ) = \pmb\sigma x $.

Here, the zero $ 0 $ is the least element of the Magari algebra. In order to distinguish the Boolean part of a Magari algebra, one writes the Magari algebra as the pair $ \langle {\mathbf A,\vartriangle } \rangle $ or $ \langle {\mathbf A, \pmb\sigma } \rangle $, where $ \mathbf A $ is a Boolean algebra.

Magari algebras arose [a8] as an attempt to treat diagonal phenomena (cf. the diagonalization lemma in [a15], [a4]) in the formal Peano arithmetic, $ { \mathop{\rm PA} } $, or other "strong enough" arithmetical theories (cf. Arithmetic, formal) in an algebraic manner. Indeed, the Lindenbaum sentence algebra [a12] of Peano arithmetic, $ {\mathcal L} { \mathop{\rm PA} } $, equipped with $\vartriangle $ defined by

$$ \vartriangle \left \| \varphi \right \| = \left \| { { \mathop{\rm Pr} } ( \lceil \varphi \rceil ) } \right \| , $$

is an example of a Magari algebra. Here $ { \mathop{\rm Pr} } ( x ) $ is the Hilbert–Bernays standard provability predicate, $ \lceil \varphi \rceil $ is the Gödel number of the sentence $ \varphi $ and $ \| \varphi \| $ means the equivalence class of the arithmetical sentences formally equivalent in Peano arithmetic to the sentence $ \varphi $. Then, the axioms 1)–2) of Magari algebra correspond to the Löb derivability conditions and 3) corresponds to the formalized Löb theorem (cf. [a15]). The diagonalization lemma is simulated with the following fixed-point theorem: For every Magari algebra and polynomial $ f ( x ) $ in its signature, with all the occurrences of $ x $ inside the scopes of $\vartriangle$, the equation $ x = f ( x ) $ can be solved in this algebra. Moreover, the solution is unique. It is called the fixed point of the polynomial $ f ( x ) $ in the given Magari algebra. Thus, considering the polynomial $ C \vartriangle x $ on $ {\mathcal L} { \mathop{\rm PA} } $, one can conclude that there is an arithmetical sentence $ \varphi $ such that

$$ \left \| \varphi \right \| = C \vartriangle \left \| \varphi \right \| = \left \| {\neg { \mathop{\rm Pr} } ( \lceil \varphi \rceil ) } \right \| , $$

i.e., $ { \mathop{\rm PA} } \vdash \varphi \leftrightarrow \neg { \mathop{\rm Pr} } ( \lceil \varphi \rceil ) $, which leads to Gödel's first incompleteness theorem; cf. Gödel incompleteness theorem.

Other examples of Magari algebras arise when one considers a pair $ \langle {Q,R } \rangle $, where $ R $ is a binary relation on $ Q $. Furthermore, denote by $ \langle {Q,R,\vartriangle } \rangle $ the Boolean algebra $ 2 ^ {Q} $ endowed with the operation

$$ \vartriangle X = \left \{ {x \in Q } : {\textrm{ for every } y \in CX, \textrm{ not } yRx } \right \} , $$

where $ X \subseteq Q $. Then $ \langle {Q,R,\vartriangle } \rangle $ is a Magari algebra if $ R $ is an irreflexive transitive relation satisfying the descending chain condition [a3]. In fact, every finite Magari algebra is isomorphic to an algebra $ \langle {Q,R,\vartriangle } \rangle $ with a finite $ Q $ and irreflexive transitive $ R $.

Let $ Q $ be the Stone space [a12] of the Boolean restriction of a Magari algebra $ \mathbf A $, which is a Stone compactum (see Boolean algebra), and let $ R \subseteq Q \times Q $ be defined as:

$$ xRy \iff \vartriangle a \in y \Rightarrow a \in x \textrm{ for every } a \in \mathbf A. $$

Then the mapping $ a \mapsto \{ {x \in Q } : {a \in x } \} $ is an embedding of $ \mathbf A $ into $ \langle {Q,R,\vartriangle } \rangle $. Moreover, $ R $ is transitive and relatively founded, i.e. every non-empty open-and-closed subset of $ Q $ contains minimal elements with respect to $ R $( the representation theorem).

There is also a duality theorem: The category of Magari algebras with homomorphisms is equivalent to the category $ \mathbf S $ defined as follows. The objects of $ \mathbf S $ are the pairs $ \langle {X,R } \rangle $, where $ X $ is a Stone compactum and $ R $ is a Boolean relation [a5] on $ X $ such that $ R ^ {- 1 } $ is transitive and relatively founded; the morphisms, say $ f : {\langle {X _ {1} ,R _ {1} } \rangle } \rightarrow {\langle {X _ {2} ,R _ {2} } \rangle } $, are the continuous mappings $ f : {X _ {1} } \rightarrow {X _ {2} } $ satisfying the equation $ f \circ R _ {1} = R _ {2} \circ f $. (Here $ \circ $ denotes composition of two relations.)

The operation $ \pmb\sigma $ defined by the axioms 1')–3') has an interesting topological interpretation: Let $ Q $ be a scattered space, i.e. a topological space in which every non-empty subset contains an isolated point, regarded along with the derived set operator $ \pmb\sigma $[a6]. Then $ \langle {2 ^ {Q} , \pmb\sigma } \rangle $ is a Magari algebra with respect to the axioms 1')–3'). Conversely, if for some set $ Q $, $ \langle {2 ^ {Q} , \pmb\sigma } \rangle $ is a Magari algebra, then $ \Omega = \{ {CX } : {\pmb\sigma X \subseteq X } \} $ is a topology on $ Q $ so that the space $ \langle {Q, \Omega } \rangle $ is scattered with the derived set operator $ \pmb\sigma $. A duality between Magari algebras in the form $ \langle {\mathbf A, \pmb\sigma } \rangle $ and relatively scattered bitopological spaces with the derived set operator has been established in [a2].

The entire set of Magari algebras constitutes a variety (see Variety of universal algebras), which is generated by its finite members. $ {\mathcal L} { \mathop{\rm PA} } $ is a generic (or functionally free) algebra of this variety, though it is proved to be non-isomorphic to the free Magari algebra of rank $ \aleph _ {0} $, $ F _ {\aleph _ {0} } $( see Free algebraic system). Moreover, up to isomorphism, $ F _ {\aleph _ {0} } $ is a proper subalgebra of $ {\mathcal L} { \mathop{\rm PA} } $. If one departs from the Zermelo–Fraenkel axiomatic set theory $ { \mathop{\rm ZF} } $, one arrives at another generic Magari algebra, $ {\mathcal L} { \mathop{\rm ZF} } $, the Lindenbaum sentence algebra of $ { \mathop{\rm ZF} } $. It is not isomorphic to either $ {\mathcal L} { \mathop{\rm PA} } $ or $ F _ {\aleph _ {0} } $, although the Boolean restrictions of the former and latter are isomorphic. Magari algebras that are Lindenbaum algebras with an additional operation related to other theories interpreting arithmetic are of current interest (cf. [a14], [a10], [a15], [a13]).

Magari algebras are an algebraic interpretation for provability logic, when the modality connective is interpreted by the operation $\vartriangle $; cf. Modal logic. This interpretation is related to the normal extensions of provability logic, because there exists a natural isomorphism between the lattice of those extensions and the lattice of varieties of Magari algebras. Introducing a new operation $ \square $ on a Magari algebra $ \mathbf A $, defined as $ \square x = x \wedge \vartriangle x $, and reading $ \square $ for $\vartriangle $, one arrives at the Grzegorczyk algebra $ \mathbf A ^ \square $. In view of the equation $ \square \vartriangle x = \vartriangle x $, one can reduce $\vartriangle $ to the open elements of $ \mathbf A ^ \square $, thereby obtaining the $\vartriangle $- pseudo-Boolean algebra $ \mathbf A ^ {\vartriangle} $. Finally, one gets the pseudo-Boolean algebra $ \mathbf A ^ \circ $[a12] by deleting $ \vartriangle $ from the signature of $ \mathbf A ^ {\vartriangle} $. These transfers give rise to the following connections: The lattice of varieties of Magari algebras and the lattice of varieties of $\vartriangle$- pseudo-Boolean algebras are isomorphic; there are semi-lattice epimorphisms from the lattice of varieties of Magari algebras onto the lattice of varieties of Grzegorczyk algebras and onto the lattice of varieties of pseudo-Boolean algebras. These connections reflect the corresponding connections between the lattices of extensions of provability logic, proof-intuitionistic logic, intuitionistic propositional logic, and the Grzegorczyk system (cf. [a11], [a7]).

References

[a1]	C. Bernardi, "The fixed-point theorem for diagonalizable algebras" Studia Logica , 34 : 3 (1975) pp. 239–251
[a2]	C. Bernardi, P. D'Aquino, "Topological duality for diagonalizable algebras" Notre Dame J. Formal Logic , 29 : 3 (1988) pp. 345–364
[a3]	G. Grätzer, "General lattice theory" , Akademie (1978)
[a4]	P. Hajek, P. Pudlak, "Metamathematics of first-order arithmetic" , Springer (1993)
[a5]	P.R. Halmos, "Algebraic logic" , Chelsea, reprint (1962)
[a6]	K. Kuratowski, "Topology" , 1 , Acad. Press & PWN (1966)
[a7]	A.V. Kuznetsov, A. Muravitsky, "On superintuitionistic logics as fragments of proof logic extensions" Studia Logica , 50 : 1 (1986) pp. 77–99
[a8]	R. Magari, "The diagonalizable algebras" Boll. Unione Mat. Ital. , 12 (1975) pp. 117–125 (suppl. fasc 3)
[a9]	R. Magari, "Representation and duality theory for diagonalizable algebras" Studia Logica , 34 : 4 (1975) pp. 305–313
[a10]	R. Magari, "Algebraic logic and diagonal phenomena" , Logic Colloquium '82 , Elsevier (1984) pp. 135–144
[a11]	A. Muravitsky, "Correspondence of proof-intuitionistic logic extensions to proof-logic extensions" Soviet Math. Dokl. , 31 : 2 (1985) pp. 345–348 (In Russian)
[a12]	H. Rasiowa, R. Sikorski, "The mathematics of metamathematics" , PWN (1970) (Edition: Third)
[a13]	V.Yu. Shavrukov, "A note on the diagonalizable algebras of PA and ZF" Ann. Pure Appl. Logic , 60 : 1–2 (1993) pp. 161–173
[a14]	C. Smoryński, "Fixed point algebras" Bull. Amer. Math. Soc. (N.S.) , 6 : 3 (1982) pp. 317–356
[a15]	C. Smoryński, "Self-reference and modal logic" , Springer (1985)
[a16]	A. Muravitsky, "Magari and 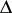-pseudo-Boolean algebras" Siberian Math. J. , 31 : 4 (1990) pp. 623–628 (In Russian)