Locally finite algebra

An algebra in which every subalgebra with finitely many generators has finite dimension over the ground field.

It is convenient to represent a locally finite algebra as the union of an increasing chain of finite-dimensional subalgebras. The class of locally finite algebras is closed with respect to taking homomorphic images and transition to subalgebras. If one restricts oneself to the consideration of associative algebras (cf. Associative rings and algebras), then the extension of a locally finite algebra by a locally finite algebra is again a locally finite algebra. Therefore, in any algebra the sum of the locally finite ideals is the largest locally finite ideal containing all locally finite ideals, and is called the locally finite radical.

In the associative case any locally finite algebra is algebraic (cf. Algebraic algebra). The converse is false (see [6]). Nevertheless, an algebraic algebra that satisfies a polynomial identity is locally finite. It is not known (1989) whether an algebraic division algebra is locally finite. There is a conjecture that a finitely-defined algebraic algebra is finite-dimensional. The Jacobson radical of a locally finite associative algebra coincides with the upper nil radical. The Jacobson radical of a locally finite Jordan algebra is also a nil ideal. Every alternative or special Jordan algebraic algebra (cf. Jordan algebra; Algebraic algebra) of bounded index (the degrees of minimal annihilating polynomials of all elements are uniformly bounded) over a field of characteristic not $2$ is locally finite. A solvable algebraic Lie algebra (the inner derivations of all elements are algebraic) is locally finite. An algebraic Lie algebra (cf. Lie algebra, algebraic) of bounded index is locally finite.

References

[1]	N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956)
[2]	I.N. Herstein, "Noncommutative rings" , Math. Assoc. Amer. (1968)
[3]	A.I. Shirshov, "On certain non-associative nil rings and algebraic algebras" Mat. Sb. , 41 (1957) pp. 381–394 (In Russian)
[4]	K. McCrimmon, "The radical of a Jordan algebra" Proc. Nat. Acad. Sci. USA , 62 (1969) pp. 671–678
[5]	S.S. Lyu, "On the splitting of locally finite algebras" Mat. Sb. , 39 (1956) pp. 385–396 (In Russian)
[6]	E.S. Golod, "On nil algebras and residually finite 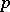-groups" Izv. Akad. Nauk SSSR Ser. Mat. , 28 (1964) pp. 273–276 (In Russian)