Kneser theorem
This page is deficient and requires revision. Please see Talk:Kneser theorem for further comments.
2020 Mathematics Subject Classification: Primary: 57R30,53C12 [MSN][ZBL]
Hellmuth Kneser's theorem on one-dimensional foliations (cf. Foliation) without singularities on closed surfaces of genus zero is a theorem that establishes properties of such a foliation depending on the presence or absence of closed leaves and describing the behaviour of non-closed leaves in domains bounded by closed leaves. The theorem is due to H. Kneser (who spoke about "regular families of curves on a surface" rather than of foliations [Kn]; for a modern account of the basic aspects of Kneser's theorem, see [Re], [AeMa]). Kneser's theorem is most often invoked in connection with trajectories of a flow without equilibrium positions on a torus or a Klein bottle (cf. Klein surface). The trajectories form a foliation of the type considered in Kneser's theorem.
A one-dimensional foliation (without singularities) on a surface is a family of non-intersecting curves ( "leaves" ) completely filling out the surface such that at each point there is a coordinate neighbourhood $U$ in which the foliation appears, in terms of corresponding local coordinates $x_1, x_2$, as the family of lines $x_2={\rm const}$ (more precisely, the connected components of intersection of the leaves with $U$ have this equation). A foliation is called orientable if it is possible to define a "positive" direction on each of its leaves (to orient the leaves) so that for different leaves these directions are compatible, that is, under a continuous passage from leaf to leaf the positive direction never changes sign. The only orientable foliations are those consisting of trajectories of certain flows without equilibrium positions.
Suppose that a direction field (field of line elements) is defined on a surface $M$, that is, with each point $x\in M$ is associated is a one-dimensional subspace $l(x)$ of the tangent plane $T_x M$ at this point (if $M$ lies in the Euclidean space, then $l(x)$ can be represented by a line tangent to $M$ at $x$, see Fig. a). If $l(x)$ depends smoothly on $x$, then the integral curves of this direction field form a one-dimensional foliation that may or may not be orientable.
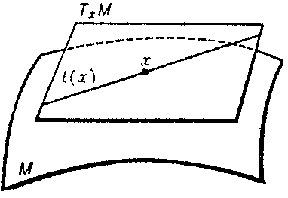
Figure: k055540a
The main content of Kneser's theorem relates to the case when the foliation possesses both closed and non-closed leaves. It states that the latter fill out the domains bounded by the former, where these domains can be of three types only (see Fig. b, where it is understood that in each of the rectangles a), b) and c) the upper side has to be glued to the lower one, with $A$ glued to $A'$ and $B$ to $B'$. For example, from a) one obtains here the "Kneser ring" , see the figure in the article Differential equations on a torus). If the surface has only one closed leaf, then in the rectangle one must glue in addition the left- and right-hand sides. a) b) c)
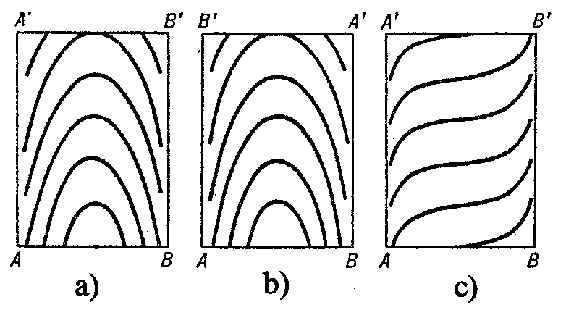
Figure: k055540b
If a non-closed leaf lying in one of these domains is extended unboundedly in one direction, then it winds itself closer and closer to the closed leaf bounding the given domain or to one of the two closed leaves bounding it. If the non-closed leaf is extended to the other side, it winds itself to the same closed leaf (on the other side) or to the second of the above-mentioned closed leaves.
There can only be a finite number of domains of type a) and b), a non-orientable domain of type b) being possible only on a Klein bottle and only for a non-orientable foliation; domains of type c) can be finite or countable in number.
Kneser also proved that the case when a foliation has no closed leaves is possible only for a non-orientable foliation on a torus and in this case there is a closed line $L$ transversal to the foliation and intersecting all the leaves. (In the general case, when it is not assumed that the leaves are smooth and the foliation is defined by some direction field, transversality is understood in the sense that at each point of $L$ there is a coordinate neighbourhood in which the leaves are defined by the equation $x_2={\rm const}$, and $L$ by the equation $x_1 = 0$.) Concerning this, see also Differential equations on a torus.
Comments
In the literature often the following consequence of the above-mentioned classification is called Kneser's theorem: Any foliation of the Klein bottle has a compact leaf.
The "Kneser rings" mentioned above are also called $2$-dimensional Reeb components. See e.g. [CaNe] and [HeHi].
References
| [AeMa] | A. Aepply, L. Markus, "Integral equivalence of vector fields on manifolds and bifurcation of differential systems" Amer. J. Math., 85 : 4 (1963) pp. 633–654 MR158138 |
| [CaNe] | C. Camacho, A.L. Neto, "Geometric theory of foliations", Birkhäuser (1985) MR0824240 Zbl 0568.57002 |
| [HeHi] | G. Hector, U. Hirsch, "Introduction to the geometry of foliations", Vieweg (1981) MR0639738 Zbl 0486.57002 |
| [Kn] | H. Kneser, "Reguläre Kurvenscharen auf Ringflächen" Math. Ann., 91 : 1–2 (1924) pp. 135–154 Zbl 50.0371.03 |
| [Re] | B.L. Reinhart, "Line elements on the torus" Amer. J. Math., 81 : 3 (1959) pp. 617–631 MR0111050 Zbl 0098.29006 |
Kneser theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kneser_theorem&oldid=29300