Inverse hyperbolic functions

Functions inverse to the hyperbolic functions. The inverse hyperbolic functions are the inverse hyperbolic sine, cosine and tangent: $\sinh ^ {-1} x$, $\cosh ^ {-1} x$, $\mathop{\rm tanh} ^ {-1} x$; other notations are: ${ \mathop{\rm arg} \sinh } x$, ${ \mathop{\rm arg} \cosh } x$, ${ \mathop{\rm arg} \mathop{\rm tanh} } x$.

The inverse hyperbolic functions of a real variable $x$ are defined by the formulas

$$\sinh ^ {-1} x = \ \mathop{\rm ln} ( x + \sqrt {x ^ {2} + 1 } ) ,\ \ - \infty < x < + \infty ,$$

$$\cosh ^ {-1} x = \ \pm \mathop{\rm ln} ( x + \sqrt {x ^ {2} - 1 } ) ,\ \ x \geq 1 ,$$

$$\mathop{\rm tanh} ^ {-1} x = \frac{1}{2} \mathop{\rm ln} \frac{1 + x }{1 - x } ,\ | x | < 1 .$$

The inverse hyperbolic functions are single-valued and continuous at each point of their domain of definition, except for $\cosh ^ {-1} x$, which is two-valued. In studying the properties of the inverse hyperbolic functions, one of the continuous branches of $\cosh ^ {-1} x$ is chosen, that is, in the formula above only one sign is taken (usually plus). For the graphs of these functions see the figure.

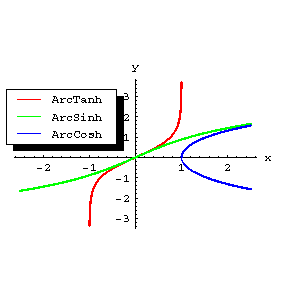
Figure: i052370a

There a number of relations between the inverse hyperbolic functions. For example,

$$\sinh ^ {-1} x = \ \mathop{\rm tanh} ^ {-1} \ \frac{x}{\sqrt {x ^ {2} + 1 } } ,\ \ \mathop{\rm tanh} ^ {-1} x = \ \sinh ^ {-1} \ \frac{x}{\sqrt {1 - x ^ {2} } } .$$

The derivatives of the inverse hyperbolic functions are given by the formulas

$$( \sinh ^ {-1} x ) ^ \prime = \ \frac{1}{\sqrt {x ^ {2} + 1 } } ,\ \ ( \cosh ^ {-1} x ) ^ \prime = \pm \frac{1}{\sqrt {x ^ {2} - 1 } } ,$$

$$( \mathop{\rm tanh} ^ {-1} x ) ^ \prime = \frac{1}{ {1 - x ^ {2} } } .$$

The inverse hyperbolic functions of a complex variable $z$ are defined by the same formulas as those for a real variable $x$, where $\mathop{\rm ln} z$ is understood to be the many-valued logarithmic function. The inverse hyperbolic functions of a complex variable are the analytic continuations to the complex plane of the corresponding functions of a real variable.

The inverse hyperbolic functions can be expressed in terms of the inverse trigonometric functions by the formulas

$$\sinh ^ {-1} z = - i { \mathop{\rm arc} \sin } i z ,$$

$$\cosh ^ {-1} z = i { \mathop{\rm arc} \cos } z ,$$

$$\mathop{\rm tanh} ^ {-1} z = - i { \mathop{\rm arc} \mathop{\rm tan} } i z .$$

Comments

The notations ${ \mathop{\rm arc} \sinh } x$, ${ \mathop{\rm arc} \cosh } x$ and ${ \mathop{\rm arc} \mathop{\rm tanh} } x$ are also quite common.

References

[a1]	M.R. Spiegel, "Complex variables" , Schaum's Outline Series , McGraw-Hill (1974)
[a2]	M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972)