Intersection homology
For non-singular complex projective algebraic varieties there are a number of (co)homological properties, such as Poincaré duality, Hodge decomposition, hard Lefschetz theorem $ \dots $
that are no longer true for the ordinary (co)homology of singular varieties. Intersection (co)homology is a modification of the usual theory designed to retain such properties for the case of singular varieties with, initially, special stress on Poincaré duality in its homological (intersection) form: Let $ M $
be a compact oriented $ 2n $-
dimensional manifold, and let $ \alpha \in H _ {i} ( M) $,
$ \beta \in H _ {2n - i } ( M) $
be homology classes with representative cycles $ a $
and $ b $
that intersect in finitely many points (such representation cycles exist). Then the number of points of intersection counted with their multiplicities is independent of $ a $
and $ b $,
and this defines a duality pairing $ H _ {i} ( M, \mathbf Q ) \times H _ {2n - i } ( M, \mathbf Q ) \rightarrow \mathbf Q $.
Let $ X $ be an $ n $- dimensional complex-analytic variety (possibly with singularities, cf. also Analytic manifold) with a Whitney stratification $ \{ X _ {j} \} $. Let $ c _ {j} $ be the codimension of $ X _ {j} $ in $ X $. Let $ \{ C _ {i} ( X) \} $ be one of the usual complexes of geometric chains on $ X $( for instance, $ C _ {i} ( X) $ could be the piecewise-linear $ i $- chains with respect to some piecewise-linear structure on $ X $). The complex of intersection chains is defined as the subcomplex $ \{ IC _ {i} ( X) \} $ satisfying the condition: a chain $ c \in IC _ {i} ( X) $ meets each singular stratum $ X _ {j} $ in a set of real dimension $ \leq i - c _ {j} $ and its boundary intersects each singular stratum $ S _ {j} $ in a set of real dimension $ \leq i - c _ {j} - 1 $.
The $ i $- th intersection homology group $ IH _ {i} ( X) $ is the $ i $- th homology group of the chain complex $ \{ IC _ {i} ( X) \} $, [a1].
There is also a sheaf-theoretic approach to intersection (co)homology. This involves perverse sheafs [a4], [a5], [a9] (cf. also $ D $- module).
There are many applications of intersection (co)homology, in particular to representation theory [a1], [a5], [a8] (for instance, a proof of the Kazhdan–Lusztig conjecture, [a7]).
Another beautiful and very useful property of smooth closed oriented Riemannian (or triangulated) manifolds is that the $ p $- th real cohomology group $ H ^ {p} ( M; \mathbf R ) $ is isomorphic to the zero eigen space of the appropriate Laplace operator (harmonic cochains). To have something similar for open manifolds, an appropriate "functional cohomology" theory has to be developed. This led to $ L _ {2} $- cohomology.
Let $ Y $ be any (in general, incomplete) Riemannian manifold with metric $ g $ and without boundary. Let $ \Lambda ^ {i} $ be the space of $ C ^ \infty $ $ i $- forms on $ Y $ and let $ d _ {i} : \Lambda ^ {i} \rightarrow \Lambda ^ {i + 1 } $ be exterior differentiation. Let $ L _ {2} ( i) $ be the space of square-integrable $ i $- forms with measurable coefficients. The $ L _ {2} $- cochain complex is now defined by $ C _ {(} 2) ^ {i} ( Y) = \{ {\alpha \in \Lambda ^ {i} \cap L _ {2} ( i) } : {d _ {i} \alpha \in L _ {2} ( i + 1) } \} $, and (one definition of) the $ i $- th $ L _ {2} $- cohomology group of $ Y $, $ H _ {(} 2) ^ {i} ( Y) $, is as follows: $ H _ {(} 2) ^ {i} ( Y) $ is the $ i $- th cohomology group of this cochain complex [a2]. In general these cohomology groups depend on the metric $ g $.
Let $ X $ be again a complex-analytic variety and let $ X \setminus \Sigma $ be its non-singular part. In many cases the $ L _ {2} $- cohomology of $ X \setminus \Sigma $( with respect to an appropriate metric) has been found to be the dual of the intersection homology of $ X $, [a1]–[a3], [a10], [a11].
References
| [a1] | R.D. MacPherson, "Global questions in the topology of singular spaces" , Proc. Internat. Congress Mathematicians (Warszawa, 1983) , 1 , PWN & Elsevier (1984) pp. 213–236 |
| [a2] | J. Cheeger, M. Goresky, R.D. MacPherson, "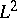 -cohomology and intersection homology of singular algebraic varieties" S.-T. Yau (ed.) , Seminar on differential geometry , Princeton Univ. Press (1982) pp. 303–340 MR0645745 Zbl 0503.14008 -cohomology and intersection homology of singular algebraic varieties" S.-T. Yau (ed.) , Seminar on differential geometry , Princeton Univ. Press (1982) pp. 303–340 MR0645745 Zbl 0503.14008 |
| [a3] | S. Zucker, "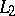 -cohomology of warped products and arithmetic groups" Invent. Math. , 70 (1982) pp. 169–218 MR0684171 Zbl 0508.20020 -cohomology of warped products and arithmetic groups" Invent. Math. , 70 (1982) pp. 169–218 MR0684171 Zbl 0508.20020 |
| [a4] | A. Borel, et al., "Intersection cohomology" , Birkhäuser (1984) MR0788176 Zbl 0553.14002 |
| [a5] | "Analyse et topologie sur les espaces singuliers I-III" Astérisque , 100–102 (1982) |
| [a6] | F.C. Kirwan, "An introduction to intersection homology theory" , Longman (1988) MR0981185 Zbl 0656.55002 |
| [a7] | J.-L. Brylinski, M. Kashiwara, "Kazhdan–Lusztig conjecture and holonomic systems" Invent. Math. , 64 (1981) pp. 387–410 MR0632980 Zbl 0473.22009 |
| [a8] | T.A. Springer, "Perverse sheafs and representation theory" P. Fong (ed.) , The Arcata Conf. Representations of Finite Groups , Proc. Symp. Pure Math. , 1 , Amer. Math. Soc. (1987) pp. 315–322 MR0933368 |
| [a9] | J.-L. Brylinski, "(Co-)homologie d'intersection et faisceaux pervers (Sem. Bourbaki 1981/1982, Exp. 585)" Astérisque , 92–93 (1982) pp. 129–158 |
| [a10] | E. Looyenga, "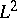 -cohomology of locally symmetric varieties" Preprint Dept. Math. Catholic Univ. Nijmegen , 8723 (1987) -cohomology of locally symmetric varieties" Preprint Dept. Math. Catholic Univ. Nijmegen , 8723 (1987) |
| [a11] | L. Saper, M. Stern, "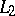 -cohomology of arithmetic varieties" Proc. Nat. Acad. Sci. USA , 84 (1987) pp. 5516–5519 MR0903789 Zbl 0653.14010 -cohomology of arithmetic varieties" Proc. Nat. Acad. Sci. USA , 84 (1987) pp. 5516–5519 MR0903789 Zbl 0653.14010 |
Intersection homology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Intersection_homology&oldid=47397