Integral-relation method

strip method

A method for solving a system of partial differential equations, based on approximately reducing a partial differential equation to a system of ordinary differential equations. It is applicable to differential equations of various types. It was introduced by A.A. Dorodnitsyn [1] as a generalization of the method of straight lines, a generalization of it with the introduction of smoothened functions was given in [2], while in [3] the method was evaluated and further developed.

Suppose one has a system of partial differential equations in divergence form

$$\tag{1 } \frac \partial {\partial x } P _ {i} ( x , y , u _ {1} \dots u _ {k} ) + \frac \partial {\partial y } Q _ {i} ( x , y , u _ {1} \dots u _ {k} ) =$$

$$= \ F _ {i} ( x , y , u _ {1} \dots u _ {k} ) ,\ i = 1 \dots k,$$

where $P _ {i}$, $Q _ {i}$, $F _ {i}$ are given functions in the independent variables $x$, $y$ and in the unknown variables $u _ {1} \dots u _ {k}$. Suppose further that a solution to (1) is sought for in the curvilinear rectangle with boundary $x = a$, $x = b$, $y = 0$, $y = \Delta ( x)$, on which $2k$ conditions are posed, and where $k$ of them are posed on $x = a$ and $x = b$. If the function $\Delta ( x)$ is unknown in advance, one only needs one additional condition. If the boundary contains singular points, then instead of corresponding boundary conditions one uses regularity conditions.

In the $N$- th approximation the domain of integration is decomposed into $N$ strips by the lines $y = y _ {n} ( x) = n \Delta ( x) / N$, $n = 1 \dots N$. For each $N$ one chooses a closed system of $N$ linearly independent functions $f _ {n} ( y)$. By multiplying each initial equation in (1) by $f _ {n} ( y)$ and after integration, with respect to $y$, across all strips, one obtains $kN$ integral relations of the form

$$\left . \frac{d}{dx} \int\limits _ { 0 } ^ { \Delta ( x) } f _ {n} ( y) P dy - \Delta ^ \prime ( x) f _ {n} ( \Delta ( x) ) P \right | _ {y = \Delta ( x) } +$$

$$+ \left . f _ {n} ( \Delta ( x)) Q \right | _ {y = \Delta ( x) } - f _ {n} ( 0) Q ( 0) +$$

$$- \int\limits _ { 0 } ^ { \Delta ( x) } f _ {n} ^ { \prime } ( y) Q dy = \int\limits _ { 0 } ^ { \Delta ( x) } f _ {n} ( y) F dy .$$

The integrals $P$, $Q$, $F$ are approximated by using interpolation formulas with respect to their values $P _ {n}$, $Q _ {n}$, $F _ {n}$ on the boundaries of the strips. The integrals participating in the integral relations have the form

$$\int\limits _ { 0 } ^ { \Delta ( x) } f _ {n} ( y) P dy \approx \Delta ( x) \sum _ { n= } 0 ^ { N } C _ {n} P _ {n} y _ {n} ( x) ,$$

where $C _ {n}$ are numerical coefficients depending on the choice of the interpolation formulas and the form of the $f _ {n} ( y)$. The result is a system of ordinary differential equations, with respect to $x$, relative to $K ( N+ 1)$ values of the unknown functions $u _ {n}$ on the entire boundaries of the strips. This system is closed by $k$ boundary conditions for $y = 0$ and $y = \Delta ( x)$.

The functions $f _ {n} ( y)$ can be chosen rather arbitrarily. Choosing $f _ {n} ( y) = \delta ( y - y _ {n} )$, $n = 1 \dots N$, i.e. delta-functions, leads to the method of straight lines. In it the derivatives with respect to $y$ are replaced by difference expressions, corresponding to the interpolation formulas chosen. When using the step-functions

$$f _ {n} ( y) = \ \left \{ \begin{array}{l} 0 \ \textrm{ for } y < y _ {n-} 1 , \\ 1 \ \textrm{ for } y _ {n-} 1 \leq y \leq y _ {n} , \\ 0 \ \textrm{ for } y > y _ {n} , \\ \end{array} \right .$$

$n = 1 \dots N$, one simply speaks of the integral-relation method, and the initial equations are integrated across each strip. Moreover, the conservation laws chosen for (1) are written as the following integral relations for the strips:

$$\frac{d}{dx} \int\limits _ { y _ {n-} 1 } ^ { {y _ n } } P dy - y _ {n} ^ \prime P ( y _ {n} )+ y _ {n-} 1 ^ \prime P ( y _ {n-} 1 ) + Q ( y _ {n} ) - Q ( y _ {n-} 1 ) =$$

$$= \ \int\limits _ { y _ {n-} 1 } ^ { {y _ n } } F dy .$$

For systems of quasi-linear hyperbolic-type equations one has investigated convergence and error of the integral-relation method [4]. In [4] one has also established results that indicate the superiority of the integral-relation method over that of straight lines. Later papers have investigated analogous results for elliptic-type equations.

The merits of the integral-relation method are, among others: the possibility of choosing the interpolation formulas and the function $f( y)$ in dependence on the behaviour of the solution; the exact integration with respect to one of the variables (a result of the divergence notation of the original equations); the simplicity of the computational algorithm; and the relatively-small amount of computer memory when calculating on a computer. In the integral-relation method one approximates by an integral: this increases the accuracy of the approximation on account of a reduction of the coefficient of the remainder term; the integral is a smoother function than the integrand, thus one may reduce the number of interpolation nodes. If the integrand has discontinuities of the first kind, then the integral is a continuous function. The integral-relation method is most efficient when the solution can be obtained with good accuracy for a small number of strips.

The approximation in two variables of the integral-relation method can be generalized to the case of equations in three variables. Approximation in two variables can be conducted also in the two-dimensional case (the domain of integration is not partitioned into strips but into subdomains then); the system of approximate equations is then a system of non-linear algebraic or transcendental equations. Elements of the integral-relation method are used in other numerical methods, e.g. in the large-particle method.

The integral-relation method is mostly used in gas dynamics, where a number of practically-important problems have been solved by using it. Three schemes of the integral-relation method have been considered here: 1) the domain of integration is partitioned by lines passing through the surface of the body and the shock waves (Fig.a); 2) the domain of integration is partitioned by lines passing through the axis of symmetry and the boundary characteristics (Fig.b); and 3) the partitioning is into subdomains by two families of intersecting lines (Fig.c).

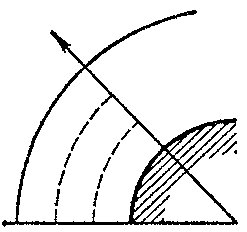
Figure: i051610a

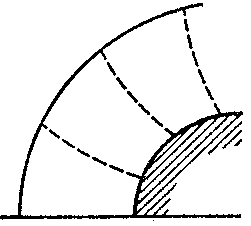
Figure: i051610b

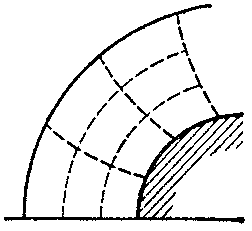
Figure: i051610c

The integral-relation method for computing supersonic flow around the fore part of a blunted body with propagating shock waves was developed in [5], in which a numerical solution to this problem in a direct formulation was obtained for the first time. The solutions for most general cases have been found (bodies of various forms; spatial flow; the flow of a real gas under equilibrium and non-equilibrium physical-chemical changes and radiations; non-stationary motion; and the flow of a viscous gas, [6]). The method has also been used for computing the potential flow of a gas [7], and for solving some mixed problems: flow in sub- and transonic parts of jets [8]. Pre-critical flow around a profile under an angle of attack with a place of the supersonic region has been considered [9]. Supersonic conic gas flow has been clarified by the integral-relation method.

The integral-relation method has found wide application in computing the flow of a viscous gas in the theory of boundary layers. In the laminar incompressible case a solution has been obtained up to the point of discontinuity [2]. Further, laminar boundary layers in a gas taking into account blowing-up or suction, radiation or heath conduction have been calculated. By the integral-relation method one has obtained solutions to the non-stationary problem of a point one-dimensional discontinuity in a gas taking counter-pressure into account, as well as in a gas with infinite conductivity in the presence of a magnetic field and in a heated gas.

References

[1]	A.A. Dorodnitsyn, "On a method for numerically solving certain nonlinear problems of aerohydrodynamics" , Proc. third All-Union Math. Congress , 3 , Moscow (1956) pp. 447–453 (In Russian)
[2]	A.A. Dorodnitsyn, "On a method for solving the laminar boundary layer equation" Zh. Priklad. Mekh. i Tekhn. Fiz. , 1 : 3 (1960) pp. 111–118 (In Russian)
[3]	O.M. Belotserkovskii, P.I. Chushkin, "A numerical method of integral relations" USSR Comp. Math. Math. Phys. , 2 (1963) pp. 823–858 Zh. Vychisl. Mat. Mat. Fiz. , 2 : 5 (1962) pp. 731–759
[4]	V.V. Bobkov, V.I. Krylov, "The method of integral relations for equations and systems of hyperbolic type" Differentsial'nye Uravneniya , 1 : 2 (1965) pp. 230–243 (In Russian)
[5]	O.M. Belotserkovskii, "Flow around a circular cylinder with a detached shockwave" Dokl. Akad. Nauk SSSR , 113 : 3 (1957) pp. 509–512 (In Russian)
[6]	O.M. Belotserkovskii, et al., "Flow of a supersonic gas around blunted bodies; theoretical and experimental investigations" , Moscow (1967) (In Russian)
[7]	P.I. Chuskin, "Subsonic gas flow around ellipses and ellipsoids" Vychisl. Mat. , 2 (1957) pp. 20–44 (In Russian)
[8]	Ya.I. Alikhashkin, A.P. Favorskii, P.I. Chushkin, "On the calculation of the flow in a plane laval nozzle" USSR Comp. Math. Math. Phys. , 3 : 6 (1963) pp. 1552–1558 Zh. Vychisl. Mat. Mat. Fiz. , 3 : 6 (1963) pp. 1130–1134
[9]	T.C. Tai, "Transonic inviscid flow over lifting airfoils by the method of integral relations" J. AIAA , 12 (1974) pp. 798–804
[10]	V.P. Korobeinikov, P.I. Chushkin, "Plane, cylindrical, and spherical explosions in a gas with counterpressure" Proc. Steklov Inst. Math. , 87 (1967) pp. 1–40 Trudy Mat. Inst. Steklov. , 87 (1966) pp. 4–34