Hysteron
Only a very simple modification of the non-linearity "hysteron" is described below. See [a1] for the general definition and an identification theorem, that is, qualitative conditions under which a "black box" is a hysteron. Consider in the $ ( x,g ) $-
plane the graphs of two continuous functions $ H _ {1} ( x ) $,
$ H _ {2} ( x ) $
satisfying the inequality $ H _ {1} ( x ) < H _ {2} ( x ) $,
$ x \in \mathbf R $.
Suppose that the set $ \Omega = \{ {\{ x,g \} } : {x \in \mathbf R, H _ {1} ( x ) \leq g \leq H _ {2} ( x ) } \} $
is partitioned into the disjoint union of the continuous family of graphs of continuous functions $ g _ \alpha ( x ) $,
where $ \alpha $
is a parameter. Each function $ g _ \alpha ( x ) $
is defined on its interval $ [ \eta _ \alpha ^ {1} , \eta _ \alpha ^ {2} ] $,
$ \eta _ \alpha ^ {1} < \eta _ \alpha ^ {2} $,
and $ g _ \alpha ( \eta _ \alpha ^ {1} ) = H _ {1} ( \eta _ \alpha ^ {1} ) $,
$ g _ \alpha ( \eta _ \alpha ^ {2} ) = H _ {2} ( \eta _ \alpha ^ {2} ) $,
that is, the end-points of the graphs of the functions $ g _ \alpha ( x ) $
belong to the union of the graphs of $ H _ {1} ( x ) $
and $ H _ {2} ( x ) $(
see Fig.a2.).

Figure: h110430a
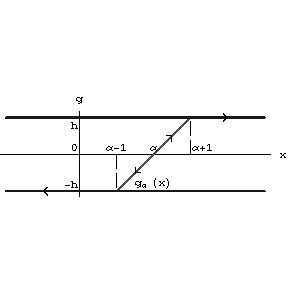
Figure: h110430b
Hysteron: Prandtl non-linearity
A hysteron is a transducer with internal states $ \xi $ from the segment $ [ 0,1 ] $ and with the following input–output operators. The variable output $ {\mathcal H} ( \xi _ {0} ) x ( t ) \equiv {\mathcal H} ( \xi _ {0} ,t _ {0} ) x ( t ) $( $ t \geq t _ {0} $) is defined by the formula
$$ {\mathcal H} ( \xi _ {0} ) x ( t ) = \left \{ \begin{array}{l} {g _ \alpha ( x ( t ) ) , \ \eta _ \alpha ^ {1} \leq x ( t ) \leq \eta _ \alpha ^ {2} , } \\ {H _ {1} ( x ( t ) ) , \ x ( t ) \leq \eta _ \alpha ^ {1} , } \\ {H _ {2} ( x ( t ) ) , \ \eta _ \alpha ^ {2} \leq x ( t ) , } \end{array} \right . $$
for monotone inputs $ x ( t ) $, $ t \geq t _ {0} $. The value of $ \alpha $ is determined by the initial state $ \xi $ to satisfy $ g _ \alpha ( x ( t _ {0} ) ) = \xi _ {0} H _ {1} ( x ( t _ {0} ) ) + ( 1 - \xi _ {0} ) H _ {2} ( x ( t _ {0} ) ) $ and the corresponding variable internal state is defined by
$$ \Xi ( \xi _ {0} ) x ( t ) = { \frac{ {\mathcal H} ( \xi _ {0} ) x ( t ) - H _ {1} ( x ( t ) ) }{H _ {2} ( x ( t ) ) - H _ {1} ( x ( t ) ) } } . $$
For piecewise-monotone continuous inputs the output is constructed by the semi-group identity. The input–output operators can then be extended to the totality of all continuous inputs by continuity (see [a1]). The operators $ {\mathcal H} ( \xi _ {0} ) x ( t ) $, $ \Xi ( \xi _ {0} ) x ( t ) $ are defined for each continuous input and each initial state. They are continuous as operators in the space of continuous functions with the uniform metric (cf. also Metric).
A hysteron is called a Prandtl non-linearity if $ H _ {1} ( x ) \equiv - h $, $ H _ {2} ( x ) \equiv h $; $ g _ \alpha = kx - \alpha $, $ \alpha - h \leq x \leq \alpha + h $, $ \alpha \in \mathbf R $. This non-linearity describes the Prandtl model of ideal plasticity with Young modulus $ k $ and elastic limits $ h $. The parallel connections of a finite numbers of such elements describe the Besseling model of elasto-plasticity and the continual counterpart describe the Ishlinskii model.
See also Hysteresis.
References
| [a1] | M.A. Krasnosel'skii, A.V. Pokrovskii, "Systems with hysteresis" , Springer (1989) (In Russian) |
Hysteron. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hysteron&oldid=47304