Gram-Charlier series
2020 Mathematics Subject Classification: Primary: 60E99 [MSN][ZBL]
A series defined by the expression
$$ \tag{1 } f _ {A} ( x) = \ f ( x) + \sum _ {k = 3 } ^ { n } a _ {k} f ^ { ( k) } ( x) $$
or
$$ \tag{2 } f _ {B} ( x) = \ \psi ( x) \sum _ {m = 0 } ^ { n } b _ {m} g _ {m} ( x), $$
where $ x $ is the normalized value of a random variable.
The series (1) is known as the Gram–Charlier series of type $ A $; here
$$ f ( x) = \ { \frac{1}{\sqrt {2 \pi }} } e ^ {- x ^ {2} /2 } , $$
$ f ^ { ( k) } $ is the $ k $-th derivative of $ f $, which can be represented as
$$ f ^ { ( k) } ( x) = \ (- 1) ^ {k} H _ {k} ( x) f ( x), $$
where $ H _ {k} ( x) $ are the Chebyshev–Hermite polynomials. The derivatives $ f ^ { ( k) } $ and the polynomials $ H _ {k} $ are orthogonal, owing to which the coefficients $ a _ {k} $ can be defined by the basic moments $ r _ {k} $ of the given distribution series. If one restricts to the first few terms of the series (1), one obtains
$$ f _ {A} ( x) = \ f ( x) + \frac{r _ {3} }{3!} f ^ { ( 3) } ( x) + $$
$$ + \frac{r _ {4} - 3 }{4! } f ^ { ( 4) } ( x) - \frac{r _ {5} - 10r _ {3} }{5! } f ^ { ( 3) } ( x) + \frac{r _ {4} - 15r _ {4} + 30 }{6! } f ^ { ( 6) } ( x). $$
The series (2) is known as a Gram–Charlier series of type $ B $; here
$$ \psi ( x) = \ \frac{\lambda ^ {x} }{x!} e ^ {- \lambda } ,\ \ x = 0, 1 \dots $$
while $ g _ {m} ( x) $ are polynomials analogous to the polynomials $ H _ {k} ( x) $.
If one restricts to the first terms of the series (2), one obtains
$$ f _ {B} ( x) = \ \frac{\lambda ^ {x} }{x! } e ^ {- \lambda } \left \{ 1 + \frac{\mu _ {2} - \lambda }{\lambda ^ {2} } \left [ \frac{x ^ {[2]} }{2 } - \lambda x ^ {[1]} + \frac{\lambda ^ {2} }{2 } \right ] \right . + $$
$$ + \left . \frac{\mu _ {3} - 3 \mu _ {2} + 2 \lambda }{\lambda ^ {3} } \left [ \frac{x ^ {[3]} }{6 } - { \frac \lambda {2} } x ^ {[2]} + \frac{\lambda ^ {2} }{2 } x ^ {[1]} - \frac{\lambda ^ {3} }{6 } \right ] \right \} . $$
Here $ \mu _ {i} $ are the central moments of the distribution, while $ x ^ {[i]} = x( x - 1) \dots ( x - i + 1) $.
Gram–Charlier series were obtained by J.P. Gram [G] and C.V.L. Charlier [Ch] in their study of functions of the form
$$ B _ {0} ( x) = \ { \frac{1}{2 \pi } } \int\limits _ {- \pi } ^ { {+ } \pi } e ^ {- itx } \phi ( t) dt. $$
These are convenient for the interpolation between the values $ B ( m) = ( n!/m! ( n - m)!) p ^ {m} q ^ {n-m} $ of the general term of the binomial distribution, where
$$ \phi ( t) = \ ( pe ^ {it} + q) ^ {n} = \ \sum _ {m = 0 } ^ { n } B ( m) e ^ {itm} $$
is the characteristic function of the binomial distribution. The expansion of $ \mathop{\rm ln} \phi ( t) $ in powers of $ t $ yields a Gram–Charlier series of type $ A $ for $ B _ {0} ( x) $, whereas the expansion of $ \mathop{\rm ln} \phi ( t) $ in powers of $ p $ yields a Gram–Charlier series of type $ B $.
References
| [G] | J.P. Gram, "Ueber die Entwicklung reeller Funktionen in Reihen mittelst der Methode der kleinsten Quadraten" J. Reine Angew. Math. , 94 (1883) pp. 41–73 |
| [Ch] | C.V.L. Charlier, "Frequency curves of type 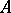 in heterograde statistics" Ark. Mat. Astr. Fysik , 9 : 25 (1914) pp. 1–17 in heterograde statistics" Ark. Mat. Astr. Fysik , 9 : 25 (1914) pp. 1–17
|
| [M] | A.K. Mitropol'skii, "Curves of distributions" , Leningrad (1960) (In Russian) |
Comments
Cf. also Edgeworth series.
References
| [Cr] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) pp. Sect. 17.6 |
Gram-Charlier series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gram-Charlier_series&oldid=52263