Geometric measure theory

An area of analysis concerned with solving geometric problems via measure-theoretic techniques. The canonical motivating physical problem is probably that investigated experimentally by J. Plateau in the nineteenth century [a4]: Given a boundary wire, how does one find the (minimal) soap film which spans it? Slightly more mathematically: Given a boundary curve, find the surface of minimal area spanning it. (Cf. also Plateau problem.) The many different approaches to solving this problem have found utility in most areas of modern mathematics and geometric measure theory is no exception: techniques and ideas from geometric measure theory have been found useful in the study of partial differential equations, the calculus of variations, harmonic analysis, and fractals.

Successes in the field include: classifying the structure of singularities in soap films (see [a18], together with the fine descriptive article [a3]); showing that the standard "double bubble" is the optimal shape for enclosing two prescribed volumes in space [a13], and developing powerful computer software for modelling the evolution of surfaces under the action of physical forces [a7].

The main reference text for the subject is [a12]. It is very densely written and [a15] serves as a useful guide through it; [a11] provides a comprehensive overview of the subject and contains a summary of its main results. For suitable introductions, see also [a17], which contains an introduction to the theory of varifolds and Allard's regularity theorem, and [a14], which includes information about tangent measures and their uses. For a slightly different slant, [a9] discusses applications of some of the ideas of geometric measure theory in the theory of Sobolev spaces and functions of bounded variation.

Many variational problems (cf. also Variational calculus) are solved by enlarging the allowed class of solutions, showing that in this enlarged class a solution exists, and then showing that the solution possesses more regularity than an arbitrary element of the enlarged class. Much of the work in geometric measure theory has been directed towards placing this informal description on a formal footing appropriate for the study of surfaces.

Rectifiability for sets.

The key concept underlying the whole theory is that of rectifiability, a measure-theoretic notion of smoothness (cf. also Rectifiable curve). A set $E$ in Euclidean $n$-space ${\bf R} ^ { n }$ is (countably) $m$-rectifiable if there is a sequence of $C ^ { 1 }$ mappings, $f _ { i } : \mathbf{R} ^ { m } \rightarrow \mathbf{R} ^ { n }$, such that

\begin{equation*} \mathcal{H} ^ { m } \left( E \backslash \bigcup _ { i = 1 } ^ { \infty } f _ { i } ( \mathbf{R} ^ { m } ) \right) = 0. \end{equation*}

It is purely $m$-unrectifiable if for all $C ^ { 1 }$ mappings $f : {\bf R} ^ { m } \rightarrow {\bf R} ^ { n }$,

\begin{equation*} \mathcal{H} ^ { m } ( E \bigcap f ( \mathbf{R} ^ { m } ) ) = 0. \end{equation*}

(Here, $\mathcal{H} ^ { m }$ denotes the $m$-dimensional Hausdorff (outer) measure, defined by

\begin{equation*} \mathcal{H} ^ { m } ( E ) = \operatorname { sup } _ { \delta > 0 } \operatorname { inf } \left\{ c _ { m } \sum _ { i } | E _ { i } | ^ { m } : \quad \begin{array} { c } { E \subset \cup _ { i } E _ { i } } \\ { | E _ { i } | < \delta \text { for all } } \ i \end{array} \right\}, \end{equation*}

where $|.|$ denotes the diameter and the constant $c _ { m}$ is chosen so that, when $m = n$, Hausdorff measure is just the usual Lebesgue measure.)

A basic decomposition theorem states that any set $E \subset {\bf R} ^ { n }$ of finite $m$-dimensional Hausdorff measure may be written as the union of an $m$-rectifiable set and a purely $m$-unrectifiable set, with the intersection necessarily having $\mathcal{H} ^ { m }$-measure zero.

In practice, the definition of rectifiability is commonly used with Lipschitz mappings replacing $C ^ { 1 }$ mappings: it may be shown that this does not change anything, see [a14], Thm. 15.21.

A standard example of a $1$-rectifiable set in the plane is a countable union of circles whose centres are dense in the unit square and with radii having a finite sum; the closure of the resulting set contains the unit square, and yet, as indicated below, the set itself still has "tangents" at $\mathcal{H} ^ { 1 }$-almost every point. An example of a purely $1$-unrectifiable set is given by taking the cross-product of the $1 / 4$-Cantor set with itself. (The $1 / 4$-Cantor set is formed by removing $2 ^ {k}$ intervals of diameter $4 ^ { - k }$, rather than $3 ^ { - k }$ as for the plain Cantor set, at each stage of its construction.)

Approximate tangents.

The main importance of the class of rectifiable sets is that it possesses many of the nice properties of the smooth surfaces which one is seeking to generalize. For example, although, in general, classical tangents may not exist (consider the circle example above), an $m$-rectifiable set will possess a unique approximate tangent at $\mathcal{H} ^ { m }$-almost every point: An $m$-dimensional linear subspace $V$ of ${\bf R} ^ { n }$ is an approximate $m$-tangent plane for $E$ at $x$ if

\begin{equation*} \operatorname { limsup } _ { r \rightarrow 0 } \frac { \mathcal{H} ^ { m } ( E \cap B ( x , r ) ) } { r ^ { m } } > 0 \end{equation*}

and for all $0 < s < 1$,

\begin{equation*} \operatorname { lim } _ { r \rightarrow 0 } \frac { \mathcal{H} ^ { m } \left( \left\{ y \in E \cap B ( x , r ) : \begin{array} { l } { \text { dist } ( y - x , V ) >} \\ {> s | y - x | }\end{array} \right\} \right) } { r^m } ) = 0. \end{equation*}

Conversely, if $E \subset {\bf R} ^ { n }$ has finite $\mathcal{H} ^ { m }$-measure and has an approximate $m$-tangent plane for $\mathcal{H} ^ { m }$-almost every $x \in E$, then $E$ is $m$-rectifiable.

Besicovitch–Federer projection theorem.

Often, one is faced with the task of showing that some set, which is a solution to the problem under investigation, is in fact rectifiable, and hence possesses some smoothness. A major concern in geometric measure theory is finding criteria which guarantee rectifiability. One of the most striking results in this direction is the Besicovitch–Federer projection theorem, which illustrates the stark difference between rectifiable and unrectifiable sets. A basic version of it states that if $E \subset {\bf R} ^ { n }$ is a purely $m$-unrectifiable set of finite $m$-dimensional Hausdorff measure, then for almost every orthogonal projection $P$ of ${\bf R} ^ { n }$ onto an $m$-dimensional linear subspace, $\mathcal{H} ^ { m } ( P ( E ) ) = 0$. (It is not particularly difficult to show that in contrast, $m$-rectifiable sets have projections of positive measure for almost every projection.) This deep result was first proved for $1$-unrectifiable sets in the plane by A.S. Besicovitch, and later extended to higher dimensions by H. Federer. Recently (1998), B. White [a19] has shown how the higher-dimensional version of this theorem follows via an inductive argument from the planar version.

Rectifiability for measures.

It is also possible (and useful) to define a notion of rectifiability for Radon (outer) measures: A Radon measure $\mu$ is said to be $m$-rectifiable if it is absolutely continuous (cf. also Absolute continuity) with respect to $m$-dimensional Hausdorff measure and there is an $m$-rectifiable set $E$ for which $\mu ( \mathbf{R} ^ { n } \backslash E ) = 0$. The complementary notion of a measure $\mu$ being purely $m$-unrectifiable is defined by requiring that $\mu$ is singular with respect to all $m$-rectifiable measures (cf. also Mutually-singular measures). Thus, in particular, a set $E$ is $m$-rectifiable if and only if $\mathcal{H} ^ { m } | _ { E }$ (the restriction of $\mathcal{H} ^ { m }$ to $E$) is $m$-rectifiable; this allows one to study rectifiable sets through $m$-rectifiable measures.

It is common in analysis to construct measures as solutions to equations, and one would like to be able to deduce something about the structure of these measures (for example, that they are rectifiable). Often, the only a priori information available is some limited metric information about the measure, perhaps how the mass of small balls grows with radius. Probably the strongest known result in this direction is Preiss' density theorem [a16] (see also [a14] for a lucid sketch of the proof). This states that if $\mu$ is a Radon measure on ${\bf R} ^ { n }$ for which $\operatorname { lim } _ { r \rightarrow 0 } \mu ( B ( x , r ) ) / r ^ { m }$ exists and is positive and finite for $\mu$-almost every $x$, then $\mu$ is $m$-rectifiable.

Preiss' main tool in proving this result was the notion of tangent measures. A non-zero Radon measure $\nu$ is a tangent measure of $\mu$ at $x$ if there are sequences $r _ { i } \searrow 0$ and $c _ { i } > 0$ such that for all continuous real-valued functions with compact support,

\begin{equation*} \operatorname { lim } _ { i \rightarrow \infty } c _ { i } \int \phi \left( \frac { y - x } { r _ { i } } \right) d \mu ( y ) = \int \phi ( y ) d \nu. \end{equation*}

Thus, an $m$-rectifiable measure will, for almost-every point, have tangent measures which are multiples of $m$-dimensional Hausdorff measure restricted to the approximate tangent plane at that point; for unrectifiable measures, the set of tangent measures will usually be much richer. The utility of the notion lies in the fact that tangent measures often possess more regularity than the original measure, thus allowing a wider range of analytical techniques to be used upon them.

Currents.

A natural approach to solving a minimal surface problem would be to take a sequence of approximating sets whose areas are decreasing and finally extract a convergent subsequence with the hope that the limit would possess the required properties. Unfortunately, the usual notions of convergence for sets in Euclidean spaces are not suited to this. The theory of currents, introduced by G. de Rham and extensively developed by Federer and W.H. Fleming in [a10] (see [a11] for a comprehensive outline of the theory and [a12] for details), was developed as a way around this obstacle for oriented surfaces. In essence, currents are generalized surfaces, obtained by viewing an $m$-dimensional (oriented) surface as defining a continuous linear functional on the space of differential forms with compact support of degree $m$ (cf. also Current). Using the duality with differential forms, it is then possible to define many natural operations on currents. For example, the boundary of an $m$-current can be defined to be the $( m - 1 )$-current, $\partial S$, which is given via the exterior derivative for differential forms (cf. also Exterior algebra) by setting

\begin{equation*} \partial S ( \phi ) = S ( d \phi ) \end{equation*}

for a differential form $\phi$ of degree $( m - 1 )$.

Of particular importance is the class of $m$-rectifiable currents: this class consists of the currents that can be written as

\begin{equation*} S ( \phi ) = \int \langle \xi ( x ) , \phi ( x ) \rangle \theta ( x ) d \mathcal{H} ^ { m } | _ { R ( x ) }, \end{equation*}

where $R$ is an $m$-rectifiable set with $\mathcal{H} ^ { m } ( R ) < \infty$, $\theta ( x )$ is a positive integer-valued function with $\int \theta d \mathcal{H} ^ { m } | _ { R } < \infty$ and $\xi ( x )$ can be written as $v_{1} \wedge \ldots \wedge v _ { m }$ with $v _ { 1 } , \dots , v _ { m }$ forming an orthonormal basis for the approximate tangent space of $R$ at $x$ for $\mathcal{H} ^ { m }$-almost every $x \in R$. (That is, $\xi ( x )$ is a unit simple $m$-vector whose associated $m$-dimensional vector space is the approximate tangent space of $R$ at $x$ for $\mathcal{H} ^ { m }$-almost every $x \in R$.) The mass of a current given in this way is defined by ${\bf M} ( S ) = \int \theta ( x ) d {\cal H} ^ { m } | _ { R ( x ) }$. If the boundary of an $m$-rectifiable current is itself an $( m - 1 )$-rectifiable current, then the $m$-current is said to be an integral current. These are the class of currents suitable for investigating Plateau's problem. The celebrated Federer–Fleming closure theorem says that on a not too wild compact domain (it should be a Lipschitz retract of some open neighbourhood of itself), those integral currents $S$ on the domain which all have the same boundary $T$, an $( m - 1 )$-current with finite mass, and for which ${\bf M} ( S )$ is bounded above by some constant $c$, form a compact set. (The topology is that generated by the integral flat distance, defined for $m$-integral currents $S _ { 1 }$, $S _ { 2 }$ by

\begin{equation*} \mathcal F _ { K } ( S _ { 1 } , S _ { 2 } ) = \operatorname { inf } \{ \mathbf M ( U ) + \mathbf M ( V ) : U + \partial V = S _ { 1 } - S _ { 2 } \}, \end{equation*}

where the infimum is over $U$ and $V$ such that $U$ is an $m$-rectifiable current on $K$ and $V$ is an $( m + 1 )$-rectifiable current on $K$.) In particular, if the constant $c$ is chosen large enough so that this set is non-empty, then one can deduce the existence of a mass-minimizing current with the given boundary $T$.

Varifolds.

The theory of currents is ideally suited for investigating oriented surfaces, but for unoriented surfaces problems arise. The theory of varifolds was initiated by F.J. Almgren and extensively developed by W.K. Allard [a1] (see also [a2] for a nice survey) as an alternative notion of surface which did not require an orientation. An $m$-varifold on an open subset $\Omega$ of ${\bf R} ^ { n }$ is a Radon measure on $\Omega \times G ( n , m )$. (Here, $G ( n , m )$ denotes the Grassmann manifold of $m$-dimensional linear subspaces of ${\bf R} ^ { n }$.) The space of $m$-varifolds is equipped with the weak topology given by saying that $\nu _ { i } \rightarrow \nu$ if and only if $\int f d \nu _ { i } \rightarrow \int f d \nu$ for all compactly supported, continuous real-valued functions on $\Omega \times G ( n , m )$. Given an $m$-varifold $\nu$, one associates a Radon measure on $\Omega$, $\| \nu \|$, by setting $\| \nu \| ( A ) = \nu ( A \times G ( n , m ) )$ for $A \subset \Omega$. As a partial converse, to an $m$-rectifiable measure $\| \mu \|$ one can associate an $m$-rectifiable varifold $\mu$ by defining for $B \subset \Omega \times G ( n , m )$,

\begin{equation*} \mu ( B ) = \| \mu \| \{ x : ( x , T _ { x } ) \in B \}, \end{equation*}

where $T _ { x }$ is the approximate tangent plane at $x$. The first variation of an $m$-varifold $\nu$ is a mapping from the space of smooth compactly supported vector fields on $\Omega$ to $\mathbf{R}$, defined by

\begin{equation*} \delta \nu ( X ) = \int \langle X ( x ) , V \rangle d \nu ( x , V ). \end{equation*}

If $\delta \nu = 0$, then the varifold is said to be stationary. The idea is that the variation measures the rate of change in the "size" of the varifold if it is perturbed slightly. A key result in the theory of varifolds is Allard's regularity theorem, which states that stationary varifolds which satisfy a growth condition (detailed below) are supported on a smooth manifold. More precisely: For all $\epsilon \in ( 0,1 )$ there are constants $\delta > 0$, $C > 0$ such that whenever $a \in \mathbf{R} ^ { n }$, $0 < R < \infty$, and $\nu$ is an $m$-dimensional stationary varifold on the open ball $U ( a , R )$ with

1) $a \in \operatorname { spt } \nu$;

2) 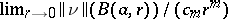existing and equal to at least one for $\| \nu \|$-almost every $x$; and

3) 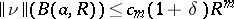, then $\operatorname { spt } ( \| \nu \| ) \cap B ( a , ( 1 - \epsilon ) R )$ is a continuously differentiable embedded $m$-submanifold of ${\bf R} ^ { n }$, and $\operatorname { dist } ( T _ { x } , T _ { y } ) \leq C ( r | x - y | ) ^ { 1 - \epsilon }$ for points in this submanifold. (The distance between the tangent spaces is given by the distance between their corresponding orthogonal projections.) This is a theorem which gives much more than just rectifiability; it gives information about the degree of smoothness as well. See [a17] for some variants and a proof of this result.

Generalization.

Given the success of the theory in Euclidean spaces, it is natural to ask whether a similar theory holds in more general spaces [a8]. There are many difficulties to be overcome, but [a5], [a6] suggest that it may be possible.

References

[a1]	W.K. Allard, "On the first variation of a varifold" Ann. of Math. , 95 (1972) pp. 417–491 MR0307015 Zbl 0252.49028
[a2]	W.K. Allard, "Notes on the theory of varifolds. Théorie des variétés minimales et applications" Astérisque , 154/5 (1987) pp. 73–93 MR0955060
[a3]	F.J. Almgren, Jr., J.E. Taylor, "The geometry of soap bubbles and soap films" Scientific Amer. , July (1976) pp. 82–93
[a4]	F.J. Almgren, Jr., "Plateau's problem: An invitation to varifold geometry" , W.A. Benjamin (1966) MR190856
[a5]	L. Ambrosio, B. Kirchheim, "Rectifiable sets in metric and Banach spaces" Math. Ann. (to appear) MR1800768 Zbl 0966.28002
[a6]	L. Ambrosio, B. Kirchheim, "Currents in metric spaces" Acta Math. (to appear) MR1794185 Zbl 1222.49057 Zbl 0984.49025
[a7]	K. Brakke, "The surface evolver V2.14" www.susqu.edu/facstaff/b/brakke/evolver/evolver.html (2000)
[a8]	G. David, S. Semmes, "Fractured fractals and broken dreams. Self-similar geometry through metric and measure" , Oxford Lecture Ser. in Math. Appl. , 7 , Clarendon Press (1997) MR1616732 Zbl 0887.54001
[a9]	L.C. Evans, R.F. Gariepy, "Measure theory and fine properties of functions" , Stud. Adv. Math. , CRC (1992) MR1158660 Zbl 0804.28001
[a10]	H. Federer, W.H. Fleming, "Normal and integral currents" Ann. of Math. , 72 : 2 (1960) pp. 458–520 MR0123260 Zbl 0187.31301
[a11]	H. Federer, "Colloquium lectures on geometric measure theory" Bull. Amer. Math. Soc. , 84 : 3 (1978) pp. 291–338 MR0467473 Zbl 0392.49021
[a12]	H. Federer, "Geometric measure theory" , Grundl. Math. Wissenschaft. , 153 , Springer (1969) MR0257325 Zbl 0176.00801
[a13]	M. Hutchings, F. Morgan, M. Ritoré, A. Ros, "Proof of the double bubble conjecture" Preprint (2000) MR1777854 Zbl 0970.53009
[a14]	P. Mattila, "Geometry of sets and measures in Euclidean spaces. Fractals and rectifiability" , Stud. Adv. Math. , 44 , Cambridge Univ. Press (1995) MR1333890 Zbl 0819.28004
[a15]	F. Morgan, "Geometric measure theory. A beginner's guide" , Acad. Press (1995) (Edition: Second) MR1326605
[a16]	D. Preiss, "Geometry of measures in ${\bf R} ^ { n }$: distribution, rectifiability, and densities" Ann. of Math. (2) , 125 : 3 (1987) pp. 537–643 MR890162
[a17]	L. Simon, "Lectures on geometric measure theory" , Proc. Centre Math. Anal. Austral. National Univ. , Centre Math. Anal. 3 Austral. National Univ., Canberra (1983) MR0756417 Zbl 0546.49019
[a18]	J.E. Taylor, "The structure of singularities in soap-bubble-like and soap-film-like minimal surfaces" Ann. of Math. (2) , 103 : 3 (1976) pp. 489–539 MR0428181 MR0428182 Zbl 0335.49032
[a19]	B. White, "A new proof of Federer's structure theorem for $k$-dimensional subsets of $\mathbf{R} ^ { N }$" J. Amer. Math. Soc. , 11 : 3 (1998) pp. 693–701