G-structure

on a manifold

A principal subbundle with structure group $ G $ of the principal bundle of co-frames on the manifold. More exactly, let $ \pi _ {k} : M _ {k} \rightarrow M $ be the principal $ \mathop{\rm GL} ^ {k} ( n) $- bundle of all co-frames of order $ k $ over an $ n $- dimensional manifold $ M $, and let $ G $ be a subgroup of the general linear group $ \mathop{\rm GL} ^ {k} ( n) $ of order $ k $. A submanifold $ P $ of the manifold of $ k $- co-frames $ M _ {k} $ defines a $ G $- structure of order $ k $, $ \pi = \pi _ {k} \mid _ {P} : P \rightarrow M $, if $ \pi $ defines a principal $ G $- bundle, i.e. the fibres of $ \pi $ are orbits of $ G $. For example, a section $ x \mapsto u _ {x} ^ {k} $ of $ \pi _ {k} $( a field of co-frames) defines a $ G $- structure $ P = \{ {gu _ {x} ^ {k} } : {x \in M, g \in G } \} $, which is called the $ G $- structure generated by this field of co-frames. Any $ G $- structure is locally generated by a field of co-frames. The $ G $- structure over the space $ V = \mathbf R ^ {n} $ generated by the field of co-frames $ x \mapsto j _ {x} ^ {k} ( \mathop{\rm id} ) $, where $ \mathop{\rm id} : V \rightarrow V $ is the identity mapping, is called the standard flat $ G $- structure.

Let $ \pi : P \rightarrow M $ be a $ G $- structure. The mapping of the manifold $ P $ into the point $ eG \in \mathop{\rm GL} ^ {k} ( n)/G $ can be extended to a $ \mathop{\rm GL} ^ {k} ( n) $- equivariant mapping $ S: M _ {k} \rightarrow \mathop{\rm GL} ^ {k} ( n)/G $, which can be considered as a structure of type $ \mathop{\rm GL} ^ {k} ( n)/G $ on $ M $. If the homogeneous space $ \mathop{\rm GL} ^ {k} ( n)/G $ is imbedded as an orbit in a vector space $ W $ admitting a linear action of $ \mathop{\rm GL} ^ {k} ( n) $, then the structure $ S $ can be considered as a linear structure of type $ W $; this is called the Bernard tensor of the $ G $- structure $ \pi $, and is often identified with it. Conversely, let $ S: M _ {k} \rightarrow W $ be a linear geometric structure of type $ W $( for example, a tensor field), whereby $ S( M _ {k} ) $ belongs to a single orbit $ \mathop{\rm GL} ^ {k} ( n) w _ {0} $ of $ \mathop{\rm GL} ^ {k} ( n) $. $ P = S ^ {-} 1 ( w _ {0} ) $ is then a $ G $- structure, where $ G $ is the stabilizer of the point $ w _ {0} $ in $ \mathop{\rm GL} ^ {k} ( n) $, and $ S $ is its Bernard tensor. For example, a Riemannian metric defines an $ O( n) $- structure, an almost-symplectic structure defines a $ \mathop{\rm Sp} ( n/2, \mathbf R ) $- structure, an almost-complex structure defines a $ \mathop{\rm GL} ( n/2, \mathbf C ) $- structure, and a torsion-free connection defines a $ \mathop{\rm GL} ( n) $- structure of the second order ( $ \mathop{\rm GL} ( n) $ is considered here as a subgroup of the group $ \mathop{\rm GL} ^ {2} ( n) $). An affinor (a field of endomorphisms) defines a $ G $- structure if and only if it has at all points one and the same Jordan normal form $ A $, where $ G $ is the centralizer of the matrix $ A $ in $ \mathop{\rm GL} ( n) $.

The elements of the manifold $ M _ {k} $ can be considered as co-frames of order 1 on $ M _ {k-} 1 $, which makes it possible to consider the natural bundle $ \pi ^ {k} : M _ {k} \rightarrow M _ {k-} 1 $ as an $ N ^ {k} $- structure of order one, where $ N ^ {k} $ is the kernel of the natural homomorphism $ \mathop{\rm GL} ^ {k} ( n) \rightarrow \mathop{\rm GL} ^ {k-} 1 ( n) $. Every $ G $- structure $ \pi : P \rightarrow M $ of order $ k $ has a related sequence of $ G $- structures of order one,

$$ P \rightarrow P _ {-} 1 \rightarrow P _ {-} 2 \rightarrow \dots \rightarrow P _ {-} k = M, $$

where $ P _ {-} i = \pi ^ {k} ( P _ {-} i+ 1 ) \subset M _ {k-} i $. Consequently, the study of $ G $- structures of higher order reduces to the study of $ G $- structures of order one. A co-frame $ u _ {x} ^ {1} \in M _ {1} $ can be considered as an isomorphism $ u _ {x} ^ {1} : T _ {x} M \rightarrow V $.

The $ 1 $- form $ \theta : TM _ {1} \rightarrow V $, assigning to a vector $ X \in T _ {u _ {x} ^ {1} } M _ {1} $ the value $ \theta _ {u _ {x} ^ {1} } ( X) = u _ {x} ^ {1} ( \pi _ {1} ) _ \star X $, is called the displacement form. In the local coordinates $ ( x ^ {i} , u _ {i} ^ {a} ) $ of $ M _ {1} $, the form $ \theta $ is expressed as $ \theta = u _ {i} ^ {a} dx ^ {i} \otimes e _ {a} $, where $ e _ {a} $ is the standard basis in $ V $.

The restriction $ \theta _ {P} $ of $ \theta $ on a $ G $- structure $ P \subset M _ {1} $ is called the displacement form of the $ G $- structure. It possesses the following properties: 1) strong horizontality: $ \theta _ {P} ( X) = 0 \iff \pi _ \star X = 0 $; and 2) $ G $- equivariance: $ \theta _ {P} \circ g = g \circ \theta _ {P} $ for any $ g \in G $.

Using the form $ \theta _ {P} $ it is possible to characterize the principal bundles with base $ M $ that are isomorphic to a $ G $- structure. Namely, a principal $ G $- bundle $ \pi : P \rightarrow M $ is isomorphic to a $ G $- structure if and only if there are a faithful linear representation $ \alpha $ of the group $ G $ in an $ n $- dimensional vector space $ V $, $ n = \mathop{\rm dim} M $, and a $ V $- valued strongly-horizontal $ G $- equivariant $ 1 $- form $ \theta $ on $ P $. Removal of the requirement that the representation $ \alpha $ be faithful gives the concept of a generalized $ G $- structure (of order one) on $ M $, namely a principal $ G $- bundle $ P \rightarrow M $ with a linear representation $ \alpha : G \rightarrow \mathop{\rm GL} ( V) $, $ \mathop{\rm dim} V = \mathop{\rm dim} M $, and a $ V $- valued strongly-horizontal $ G $- equivariant $ 1 $- form $ \theta $ on $ P $.

An example of a generalized $ G $- structure is the canonical bundle $ \pi : P \rightarrow G \setminus P $ over the homogeneous space $ G \setminus P $ of a Lie group $ P $. Here $ \alpha $ is the isotropy representation of the group $ G $, while $ \theta $ is defined by the Maurer–Cartan form of $ P $.

Let $ \pi : P \rightarrow M $ be a $ G $- structure of order one. The bundle $ \pi ^ \prime : P ^ { \prime } \rightarrow P $ of $ 1 $- jets of local sections of $ \pi $ can be considered as a $ G ^ { \prime } $- structure on $ P $, where $ G ^ { \prime } = \mathop{\rm Hom} ( V, \mathfrak g ) $ is a commutative group, $ \mathfrak g $ is the Lie algebra of $ G $, that is linearly represented in the space $ V \oplus \mathfrak g $ by the formula

$$ A( v, X) = \ ( v, X+ A( v)),\ \ A \in G ^ { \prime } ,\ \ v \in V,\ \ X \in \mathfrak g , $$

and that acts on the manifold $ P ^ { \prime } $ according to the formula

$$ H \mapsto AH = \{ {l _ {p} A( \theta ( h)) + h } : {A \in G ^ { \prime } , p = \pi ^ { \prime } ( H) , h \in H } \} , $$

where $ l _ {p} $ is the canonical isomorphism of the Lie algebra $ \mathfrak g $ of the group $ G $ onto the vertical subspace $ T _ {p} ^ {V} P = T _ {p} ( \pi ^ {-} 1 ( \pi ( p))) $. Here the element $ H \in P ^ { \prime } $ is considered as a horizontal (i.e. complementary to the vertical) subspace in $ T _ {p} P $. It defines a co-frame $ \theta _ {H} ^ \prime : T _ {p} P \mathop \rightarrow \limits ^ \approx \mathfrak g + V $, which is defined on a vertical subspace by the mapping $ l _ {p} $, and on a horizontal subspace by the mapping $ \theta _ {H} = \theta \mid _ {H} $. The vector function $ C ^ { \prime } : P ^ { \prime } \rightarrow W = \mathop{\rm Hom} ( V \wedge V, V) $, defined by the formula $ H \mapsto C _ {H} ^ { \prime } $, $ C _ {H} ^ { \prime } ( u, v) = d \theta ( \theta _ {H} ^ {-} 1 u , \theta _ {H} ^ {-} 1 v) $, is called the torsion function of the $ G $- structure $ \pi $. A section $ s: x \mapsto H _ {p(} x) $ of the bundle $ \pi \circ \pi ^ \prime : P ^ { \prime } \rightarrow M $ defines a connection on $ \pi $, while the restriction of the function $ C ^ { \prime } $ on $ s( M) $ is a function defining the coordinates of the torsion tensor of this connection relative to the field of co-frames $ p( x) $.

The mapping $ C ^ { \prime } : P ^ { \prime } \rightarrow W $ is $ G ^ { \prime } $- equivariant relative to the above-mentioned action of $ G ^ { \prime } $ on $ P $ and to the action of $ G ^ { \prime } $ on $ W $, which is defined by the formula

$$ A: w \mapsto Aw = w + \delta A, $$

where $ \delta : G ^ { \prime } \rightarrow W $, $ ( \delta A)( u, v) = A( u) v - A( v) u $. The mapping $ C: P \rightarrow G ^ { \prime } \setminus W $ induced by the mapping $ C ^ { \prime } $ is called the structure function of the $ G $- structure $ \pi $, the vanishing of $ C $ is equivalent to the existence of a torsion-free connection on $ \pi $.

The choice of a subspace $ D \subset W $ complementary to $ \delta G ^ { \prime } $ defines a subbundle $ P ^ {(} 1) = C ^ { \prime - 1 } ( D) $ of the bundle of co-frames $ \pi ^ { \prime } : P ^ { \prime } \rightarrow P $ with structure group $ G ^ {(} 1) = G ^ { \prime } \cap \mathop{\rm Ker} \delta \cong \mathfrak g \otimes V ^ \star \cap V \otimes S ^ {2} V ^ \star \subset V \otimes V ^ \star 2 $, i.e. a $ G ^ {(} 1) $- structure $ \pi ^ {(} 1) = \pi ^ \prime \mid _ {P ^ {(} 1) } : P ^ {(} 1) \rightarrow P $ on $ P $. It is called the first prolongation of the $ G $- structure $ \pi $. The $ i $- th prolongation $ \pi ^ {(} i) : P ^ {(} i) \rightarrow P ^ {(} i- 1) $ is defined by induction as the $ G ^ {(} i) $- structure on $ P ^ {(} i- 1) $, where the group $ G ^ {(} i) $ is isomorphic to the vector group $ \mathfrak g \otimes S ^ {i} V ^ \star \cap V \otimes S ^ {i+} 1 V ^ \star \subset V \otimes V ^ {\star(} i+ 1) $. The structure function $ C ^ {(} i) $ of the $ i $- th prolongation is called the structure function of $ i $- th order of the $ G $- structure $ \pi $.

The central problem of the theory of $ G $- structures is the local equivalence problem, i.e. the problem of finding necessary and sufficient conditions under which two $ G $- structures $ \pi : P \rightarrow M $ and $ \overline \pi \; : \overline{P}\; \rightarrow \overline{M}\; $ with the same structure group $ G $ are locally equivalent, i.e. a local diffeomorphism $ \phi : M \supset U \rightarrow \overline{U}\; \subset \overline{M}\; $ of the manifolds $ M $ and $ \overline{M}\; $ should exist that induces an isomorphism of $ G $- structures over the neighbourhoods $ U $ and $ \overline{U}\; $. A particular case of this problem is the integrability problem, i.e. the problem of finding necessary and sufficient conditions for the local equivalence of a given $ G $- structure and the standard flat $ G $- structure. The local equivalence problem can be reformulated as the problem of finding a complete system of local invariants of a $ G $- structure.

For an $ O( n) $- structure, which is identified with a Riemannian metric, the integrability problem was solved by B. Riemann: Necessary and sufficient conditions for integrability consist in the vanishing of the curvature tensor of the metric. The local equivalence problem was solved by E. Christoffel and R. Lipschitz: A complete system of local invariants of a Riemannian metric consists of its curvature tensor and its successive covariant derivatives (see [1]).

An approach to solving the equivalence problem is based on the concepts of a prolongation and a structure function. Every $ G $- structure $ \pi : P \rightarrow M $ of order one with structure group $ G \subset \mathop{\rm GL} ( n) $ is connected with a sequence of prolongations

$$ \dots \rightarrow P ^ {(} i) \rightarrow P ^ {(} i- 1) \rightarrow \dots \rightarrow P \mathop \rightarrow \limits ^ \pi M, $$

and a sequence of structure functions $ C ^ {(} i) $. For an $ O( n) $- structure, the structure function $ C ^ {(} 0) = C $ on $ P ^ {(} 0) = P $ is equal to 0, while the essential parts of the remaining structure functions $ C ^ {(} i) $, $ i > 0 $, are identified with the curvature tensor of the corresponding metric and its successive covariant derivatives. For $ \pi $ to be integrable it is necessary and sufficient that the structure functions $ C ^ {(} 0) \dots C ^ {(} k) $ be constant, and that their values coincide with the corresponding values of the structure functions of the standard flat $ G $- structure (see [6], [8], [9]). The number $ k $ depends only on the group $ G $. For a broad class of linear groups, especially for all irreducible groups $ G \subset \mathop{\rm GL} ( n) $ that do not belong to Berger's list of holonomy groups of spaces with a torsion-free affine connection [3], one has $ k= 0 $, and for a $ G $- structure to be integrable it is necessary and sufficient that the structure function $ C ^ {(} 0) $ vanishes, or that a torsion-free linear connection exists, preserving the $ G $- structure.

A $ G $- structure $ \pi $ is called a $ G $- structure of finite type (equal to $ k $) if $ G ^ {(} k- 1) \neq \{ e \} $, $ G ^ {(} k) = \{ e \} $. In this case $ \pi ^ {(} k) : P ^ {(} k) \rightarrow P ^ {(} k- 1) $ is a field of co-frames (an absolute parallelism), and the automorphism group of the $ G $- structure $ \pi $ is isomorphic to the automorphism group of this parallelism and is a Lie group. The local equivalence problem of these structures reduces to the equivalence problem of absolute parallelisms and has been solved in terms of a finite sequence of structure functions (see [2]). For a $ G $- structure of infinite type, the local equivalence problem remains unsolved in the general case (1984).

Two $ G $- structures $ \pi : P \rightarrow M $ and $ \pi ^ \prime : P ^ { \prime } \rightarrow M ^ { \prime } $ are called formally equivalent at the points $ x \in M $, $ x ^ \prime \in M ^ { \prime } $ if an isomorphism of the fibres $ \pi ^ {-} 1 ( x) \rightarrow \pi ^ {-} 1 ( x ^ \prime ) $ exists that can be continued to an isomorphism of the corresponding fibres of the prolongations $ P ^ {(} i) \rightarrow M $ and $ P ^ { \prime ( i) } \rightarrow M ^ { \prime } $ $ ( i \geq 0) $. Examples have been found which demonstrate that if two $ G $- structures of class $ C ^ \infty $ are formally equivalent for all pairs $ ( x, x ^ \prime ) \in M \times M ^ { \prime } $, then it does not follow, generally speaking, that they are locally equivalent [6]. In the analytic case, proper subsets $ S( M) \subset M $, $ S( M ^ { \prime } ) \subset M ^ { \prime } $ exist, which are countable unions of analytic sets, such that for any $ x \in M \setminus S( M) $, $ x ^ \prime \in M ^ { \prime } \setminus S( M ^ { \prime } ) $, the formal equivalence of two structures $ P $ and $ P ^ { \prime } $ at the points $ x, x ^ \prime $ implies that they are locally equivalent [7].

References

[1]	S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1 , Wiley (1963)
[2]	S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964)
[3]	M. Berger, "Sur les groupes d'holonomie homogène des variétés à connexion affine et des variétés riemanniennes" Bull. Soc. Math. France , 83 (1955) pp. 279–330
[4]	S.S. Chern, "The geometry of 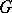-structures" Bull. Amer. Math. Soc. , 72 (1966) pp. 167–219
[5]	S. Kobayashi, "Transformation groups in differential geometry" , Springer (1972)
[6]	P. Molino, "Théorie des 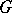-structures: le problème d'Aeequivalence" , Springer (1977)
[7]	T. Morimoto, "Sur le problème d'équivalence des structures géométriques" C.R. Acad. Sci. Paris , 292 : 1 (1981) pp. 63–66 (English summary)
[8]	I.M. Singer, S. Sternberg, "The infinite groups of Lie and Cartan. I. The transitive groups" J. d'Anal. Math. , 15 (1965) pp. 1–114
[9]	A.S. Pollack, "The integrability problem for pseudogroup structures" J. Diff. Geom. , 9 : 3 (1974) pp. 355–390