Fuzzy programming

Fuzzy programming deals with mathematical programming problems under non-probabilistic uncertainty. The idea of fuzzy programming was first given by R.E. Bellman and L.A. Zadeh [a1] and then developed by H. Tanaka [a2] and H.-J. Zimmermann [a3]. Those approaches treat soft constraints and vagueness of aspiration levels of objective function values and are called flexible programming. Later, C.V. Negoita, S. Minoiu and E. Stan [a4] dealt with the ambiguity of coefficients in mathematical programming problems by fuzzy set theory (cf. also Non-precise data). This fuzzy programming is called robust programming. D. Dubois [a5] proposed the treatment of fuzzy coefficients in fuzzy programming problems based on possibility theory. Fuzzy programming based on possibility theory is called possibilistic programming. Until now (2000), a lot of fuzzy programming approaches have been proposed, as shown in [a6], [a7], [a8].

The traditional linear programming problem can be written as (cf. also Linear programming)

\begin{equation*} \left\{ \begin{array} { l l } { \operatorname { min } } & { \mathbf{c} ^ { T } \mathbf{x} } \\ { \operatorname {s.t.} } & { A \mathbf{x} \leq \mathbf{b}. } \end{array} \right. \end{equation*}

In this problem, the decision variable vector $\mathbf{x}$ is imposed to satisfy the constraints $A \mathbf{x} \leq \mathbf{b}$ and $\mathbf{x}$ satisfies $A \mathbf{x} \leq \mathbf{b} + \varepsilon$ but $A \mathbf{x} \not\le \mathbf{b}$ is never considered as a candidate for the solution even when $\varepsilon > \mathbf 0 $ is extremely small. However, in the real world it frequently occurs that the right-hand values are not determined as rigorous restrictions and sometimes the right-hand values show the aspiration levels of the left-hand function values elicited from the decision maker. In such cases, the constraints should be treated "softly" . Fuzzy programming can treat such soft constraints. Let $B = \{ \mathbf{r} : \mathbf{r} \leq \mathbf{b} \}$; then the constraints of the above linear programming problem can be represented as $A \mathbf{x} \in B$. In fuzzy programming, replacing $B$ by a fuzzy set $\tilde{B}$ representing a "set of values approximately smaller than b" , one treats the soft constraints as $A \mathbf{x} \in \tilde { B }$, by controlling the membership value $\mu _ { B } ( A {\bf x} )$. Such a fuzzy set $\tilde{B}$ is called a fuzzy constraint.

The coefficients $\mathbf{c}$ and $A$ in the above linear programming problem are supposed to be given as real numbers. However, in real world problems one's knowledge is often insufficient to determine the coefficients as real numbers, even when the possible ranges of coefficients is known, such as "ci is about 3" . Such possible ranges can be modelled by fuzzy sets. Let $\tilde{\mathbf{c}}$ and $\tilde{A}$ be fuzzy sets representing possible ranges of $\mathbf{c}$ and $A$. Then the possible range of $A \mathbf{x}$ is obtained as the fuzzy set $\tilde{A} \mathbf{x}$ defined by the membership function:

\begin{equation*} \mu _ { \tilde{A} \mathbf{x} } ( \mathbf{z} ) = \operatorname { sup } _ { \mathbf{z} = A \mathbf{x} } \mu _ { \tilde{A} } ( A ). \end{equation*}

The possibility and necessity degrees of $A \mathbf{x} \in \tilde { B }$ are defined by:

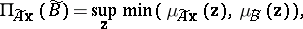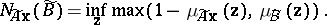The possible range of $\mathbf{c} ^ { T } \mathbf{x}$ and the possibility and necessity degrees of $\mathbf{c} ^ { \text{T} } \mathbf{x} \in \widetilde { G }$ are defined similarly, where $\tilde { G }$ is a fuzzy set.

Soft constraints with ambiguous coefficients are treated as 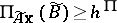and $N _ { \widetilde{A}\mathbf{x} } ( \widetilde { B } ) \geq h ^ { N }$, where $h ^ { \Pi } \in [ 0,1 ]$ and $h ^ { N } \in [ 0,1 ]$ are constants given by the decision maker. In order to treat the objective function with ambiguous coefficients, a fuzzy set $\tilde { G }$ of satisfactory values for the decision maker is established. Such a fuzzy set is called a fuzzy goal. Then the objective function is treated as $\operatorname { max} \Pi_ { \tilde{\mathbf{c}}^{ \text{T}} \mathbf{x} } ( \tilde { G } )$ or $\operatorname { max }N_{\tilde{\mathbf{c}}^{T}\mathbf{x}} ( \tilde { G } )$. Namely, in the former case, the problem is formulated as

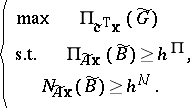It is known that such problems can be reduced to linear programming problems under certain reasonable assumptions that are applicable to real world problems [a8].

References

[a1]	R.E. Bellman, L.A. Zadeh, "Decision-making in a fuzzy environment" Management Sci. , 17B (1970) pp. 141–164
[a2]	H. Tanaka, T. Okuda, K. Asai, "On fuzzy mathematical programming" J. Cybernet. , 3 (1974) pp. 37–46
[a3]	H.-J. Zimmermann, "Description and optimization of fuzzy systems" Int. J. General Syst. , 2 (1976) pp. 209–215
[a4]	C.V. Negoita, S. Minoiu, E. Stan, "On considering imprecision in dynamic linear programming" ECECSR J. , 3 (1976) pp. 83–95
[a5]	D. Dubois, "Linear programming with fuzzy data" J.C. Bezdek (ed.) , Analysis of Fuzzy Information , 3: Applications in Engineering and Sci. , CRC (1987) pp. 241–263
[a6]	R. Słowinski, J. Teghem, "Stochastic versus fuzzy approaches to multiobjective mathematical programming under uncertainty" , Kluwer Acad. Publ. (1990)
[a7]	M. Sakawa, "Fuzzy sets and interactive multiobjective optimization" , Plenum (1993)
[a8]	M. Inuiguchi, J. Ramik, "Fuzzy linear programming: A brief review of fuzzy mathematical programming and a comparison with stochastic programming in portfolio selection problem" Fuzzy Sets and Syst. , 111 (2000) pp. 3–28