Friedrichs inequality
An inequality of the form
$$ \tag{1 } \int\limits _ \Omega f ^ { 2 } \ d \Omega \leq C \left \{ \int\limits _ \Omega \sum _ {i = 1 } ^ { n } \left ( \frac{\partial f }{\partial x _ {i} } \right ) ^ {2} \ d \Omega + \int\limits _ \Gamma f ^ { 2 } d \Gamma \right \} , $$
where $ \Omega $ is a bounded domain of points $ x = x ( x _ {1} \dots x _ {n} ) $ in an $ n $- dimensional Euclidean space with an $ ( n - 1) $- dimensional boundary $ \Gamma $ satisfying a local Lipschitz condition, and the function $ f \equiv f ( x) \in W _ {2} ^ {1} ( \Omega ) $( a Sobolev space).
The right-hand side of the Friedrichs inequality gives an equivalent norm in $ W _ {2} ^ {1} ( \Omega ) $. Using another equivalent norm in $ W _ {2} ^ {1} ( \Omega ) $, one obtains (see [2]) a modification of the Friedrichs inequality of the form
$$ \tag{2 } \int\limits _ \Omega f ^ { 2 } \ d \Omega \leq C \left \{ \int\limits _ \Omega \sum _ {i = 1 } ^ { n } \left ( \frac{\partial f }{\partial x _ {i} } \right ) ^ {2} d \Omega + \left ( \int\limits _ \Gamma f d \Gamma \right ) ^ {2} \right \} . $$
There are generalizations (see [3]–[5]) of the Friedrichs inequality to weighted spaces (see Weighted space; Imbedding theorems). Suppose that $ \Gamma \subset C ^ {(} l) $ and that the numbers $ r $, $ p $ and $ \alpha $ are real, with $ r $ being a natural number and $ 1 \leq p < \infty $. One says that $ f \in W _ {p, \alpha } ^ {r} ( \Omega ) $ if the norm
$$ \| f \| _ {W _ {p, \alpha } ^ {r} ( \Omega ) } = \ \| f \| _ {L _ {p} ( \Omega ) } + \| f \| _ {\omega _ {p, \alpha } ^ {r} ( \Omega ) } $$
is finite, where
$$ \| f \| _ {L _ {p} ( \Omega ) } = \ \left ( \int\limits _ \Omega | f | ^ {p} \ d \Omega \right ) ^ {1/p} , $$
$$ \| f \| _ {\omega _ {p, \alpha } ^ {r} ( \Omega ) } = \sum _ {| k | = r } \| \rho ^ \alpha f ^ {(} k) \| _ {L _ {p} ( \Omega ) } , $$
$$ f ^ { ( k) } = \frac{\partial ^ {| k | } f }{\partial x _ {1} ^ {k _ {1} } \dots \partial x _ {n} ^ {k _ {n} } } ,\ \ | k | = \sum _ {i = 1 } ^ { n } k _ {i} , $$
and $ \rho = \rho ( x) $ is distance function from $ x \in \Omega $ to $ \Gamma $.
Suppose that $ s _ {0} $ is a natural number such that
$$ r - \alpha - { \frac{1}{p} } \leq \ s _ {0} < r - \alpha + 1 - { \frac{1}{p} } . $$
Then, if $ \Gamma \subset C ^ {( s _ {0} + 1) } $, $ - p ^ {-} 1 < \alpha < r - p ^ {-} 1 $, $ r/2 \leq s _ {0} $, for $ f \in W _ {p, \alpha } ^ {r} ( \Omega ) $ the following inequality holds:
$$ \| f \| _ {L _ {p} ( \Omega ) } \leq \ C \left \{ \sum _ {l + s < r/2 } \left \| \left ( \left . \frac{\partial ^ {s} f }{\partial n ^ {s} } \ \right | _ \Gamma \right ) ^ {(} l) \ \right \| _ {L _ {p} ( \Gamma ) } + \| f \| _ {\omega _ {p, \alpha } ^ {r} ( \Omega ) } \right \} , $$
where $ ( \partial ^ {s} f/ \partial n ^ {s} ) \mid _ \Gamma $ is the derivative of order $ s $ with respect to the interior normal to $ \Gamma $ at the points of $ \Gamma $.
One can also obtain an inequality of the type (2), which has in the simplest case the form
$$ \| f \| _ {L _ {p} ( \Omega ) } ^ {p} \leq \ C \left ( \| f \| _ {\omega _ {p, \alpha } ^ {1} ( \Omega ) } ^ {p} + \left | \int\limits _ \Gamma u \tau d \Gamma \ \right | ^ {p} \right ) , $$
where
$$ p , \gamma > 1,\ \ - \frac{1}{p} < \alpha < 1 - \frac{1}{p} - \frac{1} \gamma , $$
$$ \tau \in L _ \gamma ( \Gamma ),\ \int\limits _ \Gamma \tau d \Gamma \neq 0. $$
The constant $ C $ is independent of $ f $ throughout.
The inequality is named after K.O. Friedrichs, who obtained it for $ n = 2 $, $ f \in C ^ {(} 2) ( \overline \Omega \; ) $( see [1]).
References
| [1] | K.O. Friedrichs, "Eine invariante Formulierung des Newtonschen Gravititationsgesetzes und des Grenzüberganges vom Einsteinschen zum Newtonschen Gesetz" Math. Ann. , 98 (1927) pp. 566–575 |
| [2] | S.L. Sobolev, "Applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian) |
| [3] | S.M. Nikol'skii, P.I. Lizorkin, "On some inequalities for weight-class functions and boundary-value problems with a strong degeneracy at the boundary" Soviet Math. Dokl. , 5 (1964) pp. 1535–1539 Dokl. Akad. Nauk SSSR , 159 : 3 (1964) pp. 512–515 |
| [4] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
| [5] | D.F. Kalinichenko, "Some properties of functions in the spaces 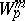 and and 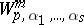 " Mat. Sb. , 64 : 3 (1964) pp. 436–457 (In Russian) " Mat. Sb. , 64 : 3 (1964) pp. 436–457 (In Russian) |
| [6] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
| [7] | L. Nirenberg, "On elliptic partial differential equations" Ann. Scuola Norm. Sup. Pisa Ser. 3 , 13 : 2 (1959) pp. 115–162 |
| [8] | L. Sandgren, "A vibration problem" Medd. Lunds Univ. Mat. Sem. , 13 (1955) pp. 1–84 |
Friedrichs inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Friedrichs_inequality&oldid=46991