Fourier coefficients of automorphic forms
Many of the applications of automorphic forms (cf. also Automorphic form) involve their Fourier coefficients. Here, the special case of holomorphic modular forms $f$ of weight $k$ for the full modular group $\operatorname{SL} ( 2 , {\bf Z} )$ will be considered. If $f ( z )$ is a such a modular form, then
\begin{equation*} f \left( \frac { a z + b } { c z + d } \right) = ( c z + d ) ^ { k } f ( z ), \end{equation*}
for all integers $a$, $b$, $c$, $d$ such that $a d - b c = 1$ and $z$ in the upper half-plane. Therefore it has period $1$ in the real part of $z$ and must have a Fourier expansion
\begin{equation*} f ( z ) = \sum _ { n = 0 } ^ { \infty } c ( n ) e ^ { 2 \pi i n z }. \end{equation*}
The numbers $c ( n )$ are the Fourier coefficients of $f$. The modular form is a cusp form if $c ( 0 ) = 0$. Some references are [a5], [a6], [a7], [a10], [a11], [a12], [a15] (see also the extensive bibliography in this).
For Eisenstein series
\begin{equation*} G _ { k } ( z ) = \sum _ { c , d \in \mathbf{Z} ^ { 2 } \backslash 0 } ( c z + d ) ^ { - k } ,\, k = 4,6,8, \dots , \end{equation*}
the non-zero Fourier coefficients are essentially divisor functions
\begin{equation*} \sigma _ { k - 1 } ( n ) = \sum _ { 0 < d | n } d ^ { k - 1 }. \end{equation*}
The theta-function associated to a positive-definite real symmetric $( n \times n )$-matrix $P$ and a point $z$ in the upper half-plane is defined by
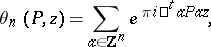 |
where $\square ^ { t } a$ denotes the transpose of the column vector $a$. One says that $P$ is an even integral matrix when $\square ^ { t } a P a$ is an even integer, for all integral column vectors $a$. In this case, $\theta _ { n } ( P , z )$ is a modular form of weight $n / 2$. Then the $m$th Fourier coefficient $r ( P , m )$ of $\theta _ { n } ( P , z )$ is the number of representations of $2 m$ as $\square ^ { t } a P a$, for some integer vector $a$. It follows from the one-dimensionality of the space of modular forms of weight $4$ that when $n = 8$,
\begin{equation*} r ( I _ { 8 } , m ) = 240 \sigma _ { 3 } ( m ), \end{equation*}
where $I_8$ denotes the identity $( 8 \times 8 )$-matrix.
There are many more examples of number-theoretically interesting Fourier coefficients. The Fourier coefficients of the inverse of the Dedekind eta-function involve the partition function $p ( n )$, which is the number of ways of writing $n$ as a sum of positive integers. The discriminant function $\Delta ( z ) = ( 60 G _ { 4 } ) ^ { 3 } - 27 ( 140 G _ { 6 } ) ^ { 2 }$ is a cusp form whose Fourier coefficients are $( 2 \pi ) ^ { 12 } \tau ( n )$, where $\tau ( n )$ is the Ramanujan tau-function (cf. also Ramanujan function). S. Ramanujan conjectured that $\tau ( m n ) = \tau ( m ) \tau ( n )$ when $m$ and $n$ are relatively prime. This was proved by L.J. Mordell. E. Hecke created the theory of Hecke operators, which gave a general framework for such results. Ramanujan also conjectured that for all prime numbers $p$ one has the inequality $| \tau ( p ) | \leq 2 p ^ { 11 / 2 }$. P. Deligne proved this conjecture as a special case of a much more general result holding for all cusp forms. This result has applications in extremal graph theory (cf. also Graph theory); [a7], [a10].
Two other conjectures are still (1998) open. Computations lead one to believe that $\tau ( n ) \neq 0$, for all $n > 0$. Writing $\tau ( p ) = 2 p ^ { 11 / 2 } \operatorname { cos } ( \phi _ { p } )$, J.-P. Serre conjectured that the angles $\phi _ { p }$ are distributed in $[ 0 , \pi ]$ with respect to the measure $( 2 / \pi ) \operatorname { sin } ^ { 2 } \phi d \phi$ (the Sato–Tate or Wigner semi-circle distribution).
The modular invariant is $J = 60 G _ { 4 } ^ { 3 } / \Delta$. The function $j = 1728 J$ has integer Fourier coefficients (writing $q = e ^ { 2 \pi i z }$)
\begin{equation*} j ( z ) = q ^ { - 1 } + 744 + 196884 q + 21493760 q ^ { 2 } +\dots . \end{equation*}
There is a surprising connection of these Fourier coefficients with the representations of the largest of the $26$ sporadic finite simple groups (the Monster; cf. also Simple finite group). All of the early Fourier coefficients of $j ( z )$ are simple linear combinations of degrees of characters of the Monster group. This led J.H. Conway [a1] to refer to the "moonshine" properties of the Monster. In 1998, R.E. Borcherds won the Fields Medal in part because he proved the Conway–Norton "moonshine conjectures" ; see [a17].
The Hecke correspondence maps a modular form $f$ with Fourier coefficients $c ( n )$ to an $L$-function (cf. also Dirichlet $L$-function) given by
\begin{equation*} L ( s ) = \sum _ { n = 1 } ^ { \infty } c ( n ) n ^ { - s } , \operatorname { Re } s > k. \end{equation*}
This $L$-function has an analytic continuation and a functional equation. The Riemann zeta-function corresponds to the simplest theta-function $\theta _ { 1 } ( 1 , z )$. But here the weight of the modular form is $1/2$ and $\theta _ { 1 }$ is not invariant under the full modular group.
If $f$ is a form of integer weight for the modular group which is an eigenfunction for all the Hecke operators, then $L ( s )$ has an Euler product. There are also converse theorems. The result is that many of the important zeta- and $L$-functions of number theory correspond to modular forms.
The Taniyama–Shimura–Weil conjecture says that the zeta-function of an elliptic curve over the rational numbers should come via the Hecke correspondence from a cusp form of weight $2$ (for a congruence subgroup of the modular group). This conjecture is intrinsically linked with the proof by A. Wiles [a16] of Fermat's last theorem (cf. also Fermat last theorem). In 1999, B. Conrad, F. Diamond and R. Taylor proved the Taniyama–Shimura–Weil conjecture when the conductor is not divisible by $27$ (see [a18]) and announced with C. Breuil a proof of the conjecture in general.
Maass wave forms (see [a8]) are eigenfunctions of the non-Euclidean Laplacian on the upper half-plane which are invariant under the modular group. Their Fourier expansions involve $K$-Bessel functions and the Fourier coefficients are more mysterious, except for those of the Eisenstein series, which are still divisor functions. Computer studies have been carried out in, e.g., [a4], [a14]. The analogue of the Ramanujan conjecture is still (1998) open.
Siegel modular forms are holomorphic functions $f ( Z )$, where $Z$ is a complex symmetric $( n \times n )$-matrix with positive-definite imaginary part, such that
\begin{equation*} f ( ( A Z + B ) ( C Z + D ) ^ { - 1 } ) = \operatorname { det } ( C Z + D ) ^ { k } f ( Z ), \end{equation*}
for all matrices $A$, $B$, $C$, $D$ with integer entries and such that with
\begin{equation*} g = \left( \begin{array} { c c } { A } & { B } \\ { C } & { D } \end{array} \right) \end{equation*}
one has $\square ^ { t } g J g = J$, where
\begin{equation*} J = \left( \begin{array} { c c } { 0 } & { I _ { n } } \\ { - I _ { n } } & { 0 } \end{array} \right), \end{equation*}
with $ { I } _ { n }$ the identity $( n \times n )$-matrix. Then $f ( Z )$ has a Fourier expansion
\begin{equation*} f ( Z ) = \sum _ { \begin{array} { c c } { 0 \leq T = \square ^ { t } T}\\{\text{semi}\square\text{integral} } \end{array}} c ( T ) e ^ { 2 \pi i \operatorname { Tr } ( T Z ) }. \end{equation*}
Here, "semi-integral" means that the diagonal entries of $T$ are integers while the off-diagonal entries are either integers or halves of integers. Examples of Siegel modular forms include Eisenstein series and theta-functions. The Siegel main theorem on quadratic forms is a consequence of a formula relating the two. The analogue of the Hecke correspondence can be discussed. See [a13], for applications to the theory of quadratic forms, or [a9].
When looking at modular forms for groups with more than one cusp, such as congruence subgroups of the modular group or Hilbert modular forms for $\operatorname{SL} ( 2 , O _ { K } )$, with $O _ { K }$ the ring of integers of a totally real algebraic number field $K$, there will be Fourier expansions at each cusp. Once more, Eisenstein series give examples. It is also possible to consider modular forms over imaginary quadratic number fields or even arbitrary number fields. See [a2]. The adelic version of the theory can be found in [a3] and [a7], for example.
References
| [a1] | J.H. Conway, "Monsters and moonshine" Math. Intelligencer , 2 (1980) pp. 165–171 MR0600222 Zbl 0452.20021 |
| [a2] | J. Elstrodt, F. Grunewald, J. Mennicke, "Groups acting on hyperbolic space" , Springer (1998) MR1483315 Zbl 0888.11001 |
| [a3] | S. Gelbart, F. Shahidi, "Analytic properties of automorphic L-functions" , Acad. Press (1988) MR0951897 Zbl 0654.10028 |
| [a4] | D. Hejhal, B. Rackner, "On the topography of Maass waveforms for $\operatorname { PSL } ( 2 , \bf Z )$" Experim. Math. , 4 (1992) pp. 275–305 MR1257286 Zbl 0813.11035 |
| [a5] | M. Koecher, A. Krieg, "Elliptische Funktionen und Modulformen" , Springer (1998) MR1711085 Zbl 0895.11001 |
| [a6] | S. Lang, "Introduction to modular forms" , Springer (1976) MR0429740 Zbl 0344.10011 |
| [a7] | W.C.W. Li, "Number theory with applications" , World Sci. (1996) MR1390759 Zbl 0849.11006 |
| [a8] | H. Maass, "Lectures on modular functions of one complex variable" , Springer (1983) MR0734485 Zbl 0539.10021 |
| [a9] | H. Maass, "Siegel's modular forms and Dirichlet series" , Lecture Notes Math. , 216 , Springer (1971) MR344198 |
| [a10] | P. Sarnak, "Some applications of modular forms" , Cambridge Univ. Press (1990) MR1102679 Zbl 0721.11015 |
| [a11] | J.-P. Serre, "A course in arithmetic" , Springer (1973) MR0344216 Zbl 0256.12001 |
| [a12] | G. Shimura, "Introduction to the arithmetic theory of automorphic functions" , Princeton Univ. Press (1971) MR0314766 Zbl 0221.10029 |
| [a13] | C.L. Siegel, "Gesammelte Abhandlungen" , I–II , Springer (1966) MR0197270 Zbl 0143.00101 |
| [a14] | H. Stark, "Fourier coefficients of Maass wave forms" R.A. Rankin (ed.) , Modular Forms , Horwood (1984) pp. 263–269 |
| [a15] | A. Terras, "Harmonic analysis on symmetric spaces and applications" , I–II , Springer (1985/1988) MR0955271 MR0791406 Zbl 0668.10033 Zbl 0574.10029 |
| [a16] | A. Wiles, "Modular elliptic curves and Fermat's last theorem" Ann. of Math. (2) , 141 (1995) pp. 443–551 |
| [a17] | R.E. Borcherds, "What is Moonshine" , Proc. Internat. Congress Mathem. (Berlin, 1998) (1998) pp. 607–615 (Doc. Math. Extra Vol. 1; see also pp. 99–108) MR1660657 Zbl 1003.11017 |
| [a18] | B. Conrad, F. Diamond, R. Taylor, "Modularity of certain potentially Barsotti–Tate Galois representations" J. Amer. Math. Soc. , 12 (1999) pp. 521–567 MR1639612 Zbl 0923.11085 |
Fourier coefficients of automorphic forms. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier_coefficients_of_automorphic_forms&oldid=56147