Finsler space, generalized
A space with an internal metric, subject to certain restrictions on the behaviour of shortest curves (that is, curves with length equal to the distance between their ends). Such spaces include $ G $-
spaces (see Geodesic geometry) and, in particular, Finsler spaces (cf. Finsler geometry), so that the spaces in question can be characterized as a generalization of Finsler, and not just of Riemannian spaces. Generalized Finsler spaces differ from Finsler spaces not only in their greater generality, but also in the fact that they are defined and investigated starting from a metric, without coordinates.
A $ G $- space can be defined as a finitely compact space (that is, closed bounded sets in it are compact) with an internal metric in which shortest curves are locally uniquely extendable, that is, such that the following two conditions are satisfied.
1) Existence of an extension: Each point has a neighbourhood $ U $ such that for every shortest curve $ AB \subset U $ there is a shortest curve $ AC \supset AB $, $ C \neq B $.
2) Uniqueness of the extension, or "non-superposition" : If $ AC \supset AB $ and $ AC _ {1} \supset AB $, then either $ AC \supset AC _ {1} $ or $ AC _ {1} \supset AC $. The actual existence of shortest curves is ensured by finite compactness: In a finitely compact space with an internal metric any two points can be joined by a shortest curve. The uniqueness of the extension implies the local uniqueness of the shortest curve with given end-points. Thus, a $ G $- space can be characterized as a finitely compact space in which any two points can be joined by a shortest curve that locally possesses the main properties of straight line-segments.
For spaces with an internal metric, finite compactness is equivalent to the combination of local compactness and completeness (see [3]).
A $ G $- space is topologically homogeneous, that is, for any two points in it there is a homeomorphism of the space onto itself that maps one of these points to the other. Moreover, this homeomorphism can be chosen to be isotopic to the identity. $ G $- spaces of dimension $ \leq 3 $ are topological manifolds. A finite-dimensional $ G $- space has the property of invariance of domains, that is, if one of two homeomorphic subsets of it is open, then so is the other. It is not known (1984) whether every $ G $- space is finite-dimensional.
A set $ V $ in a space $ M $ with an internal metric is called convex if any two points $ X, Y \in V $ can be joined by a shortest curve $ XY $ and if every such shortest curve is contained in $ V $. A space $ M $ has the property of convexity of small spheres if every point of it has a neighbourhood such that every sphere contained in it is convex. Every $ G $- space with convex small spheres is finite-dimensional. In particular, this is true for $ G $- spaces of curvature $ \leq K $( see Riemannian space, generalized) and for $ G $- spaces of non-positive curvature (in the sense of Busemann). The latter means that locally in every triangle consisting of shortest curves the length of a middle line of the triangle is not greater than half the corresponding side. The finite-dimensionality is also true for $ G $- spaces of curvature $ \geq K $( see [4]).
A motion of a metric space is a mapping of the space onto itself that preserves distances between points. The group of all motions of a compact $ G $- space with the compact-open topology is a Lie group (see [1]). This is also true in the non-compact case if the $ G $- space satisfies the condition of convexity of small spheres (see [6]).
A metric space is homogeneous if for any two points of the space there is a motion mapping one of the points to the other. A motion $ \Phi $ of a metric space is called a symmetry relative to a point $ p $ if $ \Phi ( \Phi ( x)) = x $ for all $ x $, and if $ p $ is an isolated fixed point of $ \Phi $. A space is called symmetric if for any point of it there is a symmetry relative to that point. Symmetric $ G $- spaces are homogeneous and satisfy the condition of convexity of small spheres. The group of all motions of a homogeneous $ G $- space is a Lie group, and the space itself is a topological manifold (see [5]). A symmetric $ G $- space is a Finsler space with convex indicatrices. If, in addition, there is an angle between any two shortest curves emanating from one point, then the space is a symmetric Riemannian space.
Let $ M $ be a metric space with metric $ \rho $, endowed with a group structure. The metric $ \rho $ is called left-invariant if the mapping of left multiplication by an element $ g $ is a motion of the space. A right-invariant metric is defined similarly. A metric that is both left- and right-invariant is called bi-invariant. A $ G $- space that is a group with a bi-invariant metric is a symmetric Lie group (see [5]), and consequently a Finsler space. This is a generalization of a well-known result for Riemannian spaces.
References
| [1] | A.D. Aleksandrov, "Die innere Geometrie der konvexen Flächen" , Akademie Verlag (1955) (Translated from Russian) |
| [2] | A.D. Aleksandrov, "A theorem on triangles in a metric space and some of its applications" Trudy Mat. Inst. Steklov. , 38 (1951) pp. 5–23 (In Russian) |
| [3] | A.D. Aleksandrov, "Ueber eine Verallgemeinerung der Riemannsche Geometrie" Schrift. Inst. Math. Deutsch. Akad. Wiss. , 1 (1957) pp. 33–84 |
| [4] | V.N. Berestovskii, "Introduction of a Riemann structure into certain metric spaces" Siberian Math. J. , 16 : 4 (1975) pp. 499–507 Sibirsk. Mat. Zh. , 16 : 4 (1975) pp. 651–652 |
| [5] | I.G. Nikolaev, "Space of directions at a point in a space of curvature not greater than 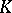 " Siberian Math. J. , 19 : 6 (1978) pp. 944–948 Sibirsk. Mat. Zh. , 19 : 6 (1978) pp. 1341–1348 " Siberian Math. J. , 19 : 6 (1978) pp. 944–948 Sibirsk. Mat. Zh. , 19 : 6 (1978) pp. 1341–1348 |
| [6] | I.G. Nikolaev, "Solution of Plateau's problem in spaces of curvature not greater than 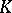 " Siberian Math. J. , 20 : 2 (1979) pp. 246–251 Sibirsk. Mat. Zh. , 20 : 2 (1979) pp. 345–353 " Siberian Math. J. , 20 : 2 (1979) pp. 246–251 Sibirsk. Mat. Zh. , 20 : 2 (1979) pp. 345–353 |
| [7] | Yu.G. Reshetnyak, "On the theory of spaces with curvature no greater than 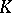 " Mat. Sb. , 52 : 3 (1960) pp. 789–798 (In Russian) " Mat. Sb. , 52 : 3 (1960) pp. 789–798 (In Russian) |
| [8] | Yu.G. Reshetnyak, "Inextensible mappings in a space of curvature not greater than 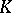 " Siberian Math. J. , 9 : 4 (1968) pp. 683–689 Sibirsk. Mat. Zh. , 9 : 4 (1968) pp. 918–927 " Siberian Math. J. , 9 : 4 (1968) pp. 683–689 Sibirsk. Mat. Zh. , 9 : 4 (1968) pp. 918–927 |
| [9] | H. Busemann, "The geometry of geodesics" , Acad. Press (1955) |
| [10] | H. Busemann, "Recent synthetic differential geometry" , Springer (1970) |
| [11] | S. Cohn-Vossen, "Existenz kürzester Wege" Compos. Math. , 3 (1936) pp. 441–452 |
| [12] | V.N. Berestovskii, "The finite-dimensionality problem for Busemann 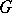 -spaces" Siberian Math. J. , 18 : 1 (1977) pp. 159–161 Sibirsk. Mat. Zh. , 18 : 1 (1977) pp. 219–221 -spaces" Siberian Math. J. , 18 : 1 (1977) pp. 159–161 Sibirsk. Mat. Zh. , 18 : 1 (1977) pp. 219–221 |
| [13] | V.N. Berestovskii, "Homogeneous Busemann 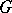 -spaces" Siberian Math. J. , 23 : 2 (1982) pp. 141–150 Sibirsk. Mat. Zh. , 23 : 1 (1982) pp. 3–15 -spaces" Siberian Math. J. , 23 : 2 (1982) pp. 141–150 Sibirsk. Mat. Zh. , 23 : 1 (1982) pp. 3–15 |
| [14] | J. Szenthe, "Homogeneous spaces with intrinsic metric" Magyar Tud. Akad. Mat. Fiz. Oszt. Közl. , 13 (1963) pp. 125–132 (In Hungarian) |
| [15] | V.N. Berestovskii, "Generalized symmetric spaces" Siberian Math. J. , 26 : 2 (1985) pp. 159–170 Sibirsk. Mat. Zh. , 26 : 2 (1985) pp. 3–17 |
| [16] | H. Busemann, B.B. Phadke, "Spaces with distinguished geodesics" , M. Dekker (1987) |
Comments
References
| [a1] | M. Gromov, "Structures métriques des espaces riemanniennes" , F. Nathan (1981) (Translated from Russian) |
Finsler space, generalized. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Finsler_space,_generalized&oldid=46932