Euler operator

Euler–Lagrange operator

A fundamental object, $\cal E$, in the calculus of variations (cf. also Variational calculus), used to formulate the system of partial differential equations, called the Euler–Lagrange equations or the variational equations, that the extremals for variational problems must satisfy (cf. also Euler–Lagrange equation).

In essence, to each Lagrangian $L$, the Euler operator assigns a geometric object $\mathcal{E} ( L )$ whose components $\mathcal{E} ^ { a } ( L )$, $a = 1 , \dots , m$, are the expressions for the Euler–Lagrange equations.

For trivial fibre bundles (or locally on appropriate charts) and for first-order Lagrangians, the Euler operator is easy to describe. Thus, suppose $U \subseteq \mathbf{R} ^ { n }$, $F \subseteq {\bf R} ^ { m }$ are open sets, $M = \overline { U }$ is compact, and $E = M \times F$ is the trivial fibre bundle (cf. also Fibre space) over $M$ with fibre $F$ and projection $\pi : E \rightarrow M$ given by $\pi ( x , y ) = x$. Here $x = ( x _ { 1 } , \ldots , x _ { n } )$ and $y = ( y ^ { 1 } , \dots , y ^ { m } )$. Then the first-order jet bundle for $E$ is the set

\begin{equation*} E ^ { 1 } = J ^ { 1 } ( E ) = M \times F \times \mathbf{R} ^ { n m }, \end{equation*}

whose points are $( x , y , y ^ { \prime } )$ where 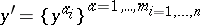. A first-order Lagrangian is a real-valued function $L : E ^ { 1 } \rightarrow \mathbf{R}$ that has continuous partial derivatives up to the second order and determines a variational problem as follows.

The set of sections $\Gamma ( E )$ consists of functions $\sigma : M \rightarrow E$ of the form

\begin{equation*} \sigma ( x ) = ( x , y ( x ) ) \end{equation*}

where $y : M \rightarrow F$ is twice continuously differentiable. Each section $\sigma$ has a $1$-jet $\sigma ^ { 1 }$, which is the section $\sigma ^ { 1 } : M \rightarrow E ^ { 1 }$ given by

\begin{equation*} \sigma ^ { 1 } ( x ) = ( x , y ( x ) , y ^ { \prime } ( x ) ), \end{equation*}

where 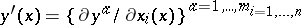. With this notation, the variational problem associated with the Lagrangian $L$ is to determine the extreme values of the function $\mathcal{A} : \Gamma ( E ) \rightarrow \mathbf{R}$, which is the action (or action integral) for $L$:

\begin{equation*} \mathcal{A} ( \sigma ) = \int _ { M } L ( \sigma ^ { 1 } ( x ) ) d x = \int _ { M } L ( x , y ( x ) , y ^ { \prime } ( x ) ) d x. \end{equation*}

In the trivial bundle setting, it is an easy exercise to derive the partial differential equations, called the Euler–Lagrange equations (cf. Euler–Lagrange equation), that any extremal $\sigma$ of $\mathcal{A}$ must satisfy. This derivation is given here since it will clarify the difficulties in obtaining the global, or intrinsic, version of these equations when the fibre bundle $E$ is not trivial.

For simplicity, assume $M = [ a , b ]$ is a bounded closed interval in $\mathbf{R}$ and $m = 1$. Suppose that $\mathcal{A}$ has a maximum or minimum value at $\sigma$. Let $\sigma _ { t }$ be the section

\begin{equation*} \sigma _ { t } ( x ) = ( x , y ( x ) + t z ( x ) ), \end{equation*}

where $z: M \rightarrow F$ is any twice continuously differentiable function with compact support in $M$ (so, in particular, $z ( a ) = 0 = z ( b )$). Then for a suitably chosen $\epsilon > 0$, the function $f : ( - \epsilon , \epsilon ) \rightarrow \mathbf{R}$ defined by

\begin{equation*} f ( t ) = A ( \sigma _ { t } ) = \int _ { a } ^ { b } L ( x , y ( x ) + t z ( x ) , y ^ { \prime } ( x ) + t z ^ { \prime } ( x ) ) d x \end{equation*}

has a maximum or minimum value at $t = 0$. Consequently,

\begin{equation*} 0 = f ^ { \prime } ( 0 ) = \end{equation*}

\begin{equation*} = \int _ { a } ^ { b } \left[ \frac { \partial L } { \partial y } ( \sigma ^ { 1 } ( x ) ) z ( x ) + \frac { \partial L } { \partial y ^ { \prime } } ( \sigma ^ { 1 } ( x ) ) z ^ { \prime } ( x ) \right] d x = \end{equation*}

\begin{equation*} = \int _ { a } ^ { b } \left[ \frac { \partial L } { \partial y } ( \sigma ^ { 1 } ( x ) ) - \frac { d } { d x } \left( \frac { \partial L } { \partial y ^ { \prime } } ( \sigma ^ { 1 } ( x ) ) \right) \right] z ( x ) d x = \end{equation*}

\begin{equation*} = \int _ { a } ^ { b } {\cal E} ( L ) ( \sigma ^ { 2 } ( x ) ) z ( x ) d x. \end{equation*}

In the last equation, $\mathcal{E} ( L )$ denotes the function on the second-order jet bundle $E ^ { 2 }$ defined by

\begin{equation*} \mathcal{E} ( L ) = \frac { \partial L } { \partial y } - D \left( \frac { \partial L } { \partial y ^ { \prime } } \right), \end{equation*}

where $D$ is the differential operator

\begin{equation*} D = \frac { \partial } { \partial x } + y ^ { \prime } \frac { \partial } { \partial y } + y ^ { \prime \prime } \frac { \partial } { \partial y ^ { \prime } }. \end{equation*}

In this setting, then, the Euler operator is $L \mapsto \mathcal{E} ( L )$. The differential operator $D$ is called the total derivative operator.

It is important to note that the next to the last equation above comes from integrating by parts and uses the assumption that $z$ vanishes on the boundary of $[ a , b ]$.

From the arbitrariness of the variation function $z$ (up to the stated conditions), the above shows that $\sigma$ must satisfy the second-order partial differential equation

\begin{equation*} \mathcal{E} ( L ) ( \sigma ^ { 2 } ( x ) ) = 0, \end{equation*}

for all $x \in ( a , b )$. This is the Euler–Lagrange equation for this special case.

For the higher-dimensional cases $n > 1$, $m > 1$ (but still first-order Lagrangians), the above variational argument is entirely similar and one can show than each extremal $\sigma$ must satisfy the system of partial differential equations

\begin{equation*} {\cal E} ^ { a } ( L ) ( \sigma ^ { 2 } ( x ) ) = 0, \end{equation*}

$a = 1 , \dots , m$, for all $x \in M$. Here,

\begin{equation*} \mathcal{E} ^ { a } ( L ) = \frac { \partial L } { \partial y ^ { a } } - D _ { i } \left( \frac { \partial L } { \partial y ^ { a _ { i } } } \right), \end{equation*}

and $D_i$ is the differential operator

\begin{equation*} D _ { i } = \frac { \partial } { \partial x _ { i } } + y ^ { b _ { i } } \frac { \partial } { \partial y ^ { b } } + y ^ { b _ { i j } } \frac { \partial } { \partial y ^ { b _ { j } } }. \end{equation*}

These expressions involve (Einstein) summation on repeated indices, as is customary (cf. also Einstein rule). Again, the operator $D_i$ is called the total derivative operator and the Euler operator for this setting is the mapping $\mathcal E ( L ) = ( \mathcal E ^ { 1 } ( L ) , \ldots , \mathcal E ^ { m } ( L ) )$, assigning to each first-order Lagrangian a function on the second-order jet bundle.

Within the trivial bundle setting (or on local charts, for non-trivial bundles), the Euler operator for higher-order Lagrangians $L : E ^ { k } \rightarrow \bf R$, $k > 1$, is also easy to describe. This requires the multi-index notation.

A multi-index is an $n$-tuple $\alpha = ( \alpha _ { 1 } , \ldots , \alpha _ { n } )$ of non-negative integers and the order of $\alpha$ is $| \alpha | = \alpha _ { 1 } + \ldots + \alpha _ { n }$. Also,

\begin{equation*} ( \frac { \partial } { \partial x } ) ^ { \alpha } = ( \frac { \partial } { \partial x _ { 1 } } ) ^ { \alpha _ { 1 } } \dots ( \frac { \partial } { \partial x _ { n } } ) ^ { \alpha _ { n } }. \end{equation*}

With this notation, a point in the $k$th-order jet bundle $E ^ { k } = M \times F \times F ^ { ( 1 ) } \times \ldots F ^ { ( k ) }$ is denoted by

\begin{equation*} ( x , y , y ^ { \prime } , \dots , y ^ { ( k ) } ), \end{equation*}

where $y ^ { ( r ) } = \{ y _ { \alpha } ^ { a } \} _ { | \alpha | = r } ^ { a = 1 , \ldots , m }$. For a section $\sigma ( x ) = ( x , y ( x ) )$, its $k$-jet $\sigma ^ { k } : M \rightarrow E ^ { k }$ is given by

\begin{equation*} \sigma ^ { k } ( x ) = ( x , y ( x ) , y ^ { \prime } ( x ) , \ldots , y ^ { ( k ) } ( x ) ), \end{equation*}

where

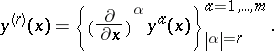Using a variational argument similar to that above, but now integrating by parts $k$ times, one can show that if the action $\mathcal{A} ( \sigma ) = \int _ { M } L ( \sigma ^ { k } ( x ) ) d x$ has a local maximum or minimum value at $\sigma$, then $\sigma$ must satisfy the system of partial differential equations

\begin{equation*} \mathcal{E} ^ { a } ( L ) ( \sigma ^ { 2 k } ( x ) ) = 0, \end{equation*}

$a = 1 , \dots , m$, for all $x \in M$. Here,

\begin{equation*} \mathcal{E} ^ { a } ( L ) = \sum _ { | \alpha | = 0 } ^ { k } ( - 1 ) ^ { | \alpha | } D ^ { \alpha } \left( \frac { \partial L } { \partial y _ { \alpha } ^ { a } } \right), \end{equation*}

where $D ^ { \alpha } = D _ { 1 } ^ { \alpha _ { 1 } } \ldots D _ { n } ^ { \alpha _ { n } }$, and $D_i$ is the total derivative operator:

\begin{equation*} D _ { i } = \frac { \partial } { \partial x _ { i } } + \sum _ { | \alpha | = 0 } ^ { 2 k } y _ { \alpha + e _ { i } } ^ { b } \frac { \partial } { \partial y _ { \alpha } ^ { b } }. \end{equation*}

Note that $e _ { i }$ is the multi-index of all zeros except for a $1$ in the $i$th position.

In the general setting, the intrinsic construction of the Euler operator is more complicated and many different approaches occur in the literature. See [a1], [a2], [a3], [a4], [a5]. One approach realizes $\mathcal{E} ( L )$ as a certain $n$-form-valued $1$-form on $E ^ { 2 k }$ which is globally defined and has, in any chart, the local expression

\begin{equation*} \mathcal{E} ( L ) = \mathcal{E} ^ { a } ( L ) \omega ^ { a } \bigotimes \Delta, \end{equation*}

using Einstein summation, the $\omega ^ { a}$-s are the local contact $1$-forms, $\omega ^ { a } = d y ^ { a } - y _ { e _ { i } } ^ { a } d x _ { i }$, and $\Delta = \gamma d x _ { 1 } \wedge \ldots \wedge d x _ { n }$ is a volume form on the base space $M$. Because of the function $\gamma : M \rightarrow {\bf R}$ in the local expression for the volume form, the components in the local expression of $\mathcal{E} ( L )$ are slightly modified from above to

\begin{equation*} \mathcal{E} ^ { a } ( L ) = \sum _ { | \alpha | = 0 } ^ { k } ( - 1 ) ^ { | \alpha | } \gamma ^ { - 1 } D ^ { \alpha } \left( \gamma \frac { \partial L } { \partial y _ { \alpha } ^ { a } } \right). \end{equation*}

This approach to the Euler operator is briefly described as follows.

Suppose that $\pi : E \rightarrow M$ is a fibre bundle with $m$-dimensional fibre and base space $M$ which is a smooth, $n$-dimensional manifold with volume form $\Delta$. For simplicity of exposition, assume that $M$ is compact. The $k$th-order jet bundle $E ^ { k } = \left\{ [ \sigma ] _ { x } ^ { k } : x \in M , \sigma \in \Gamma _ { x } ( E ) \right\}$ consists of equivalence classes of local sections at $x \in M$, all of whose partial derivatives up to order $k$ are the same at $x$. There are naturally defined projections $\pi ^ { k } : E ^ { k } \rightarrow M$ and $\pi _ { r } ^ { k } : E ^ { k } \rightarrow E ^ { r }$ and it is common, to simplify the notation, to identify a differential form $\theta$ on $E ^ { r }$ with its pullback $\pi _ { r } ^ { k * } ( \theta )$ to $E ^ { k }$. Thus, $\Delta = \pi ^ { k ^ { * } } ( \Delta )$ and, for a Lagrangian $L : E ^ { k } \rightarrow \bf R$, the action integral can be written as

\begin{equation*} {\cal A} ( \sigma ) = \int _ { M } L \circ \sigma ^ { k } \Delta = \int _ { M } \sigma ^ { k ^ { * } } ( L \Delta ). \end{equation*}

To make a variation in the action, as was done above in the trivial case, suppose $Z$ is a vertical vector field on $E$ (i.e. $d \pi _ { e } Z _ { e } = 0$ for all $e \in E$) and that $\phi _ { t }$ is its corresponding flow. Then the prolongation $Z^k$ of $Z$ to a vertical vector field on $E ^ { k }$ has flow $\phi _ { t } ^ { k }$ (cf. also Prolongation of solutions of differential equations). Letting $\sigma _ { t } = \phi _ { t } \circ \sigma$, one has $\sigma _ { t } ^ { k } = \phi _ { t } ^ { k } \circ \sigma ^ { k }$, and consequently

\begin{equation*} \left. \frac { d } { d t } {\cal A} ( \sigma _ { t } ) \right| _ { t = 0 } = \left. \frac { d } { d t } \int _ { M } \sigma ^ { k ^ { * } } \phi _ { t } ^ { k ^ { * } } ( L \Delta ) \right| _ { t = 0 } = \end{equation*}

\begin{equation*} = \int _ { M } \sigma ^ { k ^ { * } } \mathcal{L} _ { Z ^ { k } } ( L \Delta ). \end{equation*}

Here, $\mathcal{L} _ { \text{Z} ^ { k } } ( L , \Delta ) = Z ^ { k }\lrcorner d L \Delta + d ( Z ^ { k } \lrcorner L \Delta )$ is the Lie derivative of $L \Delta$. Suppose now that $Z$ has compact support contained in the interior of $\sigma ( M )$. Use this together with the Stokes theorem to reduce the variation of the action to

\begin{equation*} \frac { d } { d t } {\cal A} ( \sigma _ { t } ) | _ { t = 0 } = \int _ { M } \sigma ^ { k ^ { * } } ( Z ^ { k } \lrcorner d L \Delta ) = \end{equation*}

\begin{equation*} = \int _ { M } \sigma ^ { k + 1* } [ \Omega ( d L \Delta ) ( Z ^ { k + 1 } ) ]. \end{equation*}

The latter equation results from using the variational operator $\Omega$, which maps $n + 1$-forms on $E ^ { r }$ into $n$-form-valued contact $1$-forms on $E ^{r+1} $. For the case under consideration here, $\Omega ( d L \Delta )$ has, on each chart, a component expression:

\begin{equation*} \Omega ( d L \Delta ) = \sum _ { | \alpha | = 0 } ^ { k } \frac { \partial L } { \partial y _ { \alpha } ^ { a } } \omega _ { \alpha } ^ { a } \bigotimes \Delta . \end{equation*}

Consequently, the component expression for the integrand of the first variation is

\begin{equation*} \sum _ { | \alpha | = 0 } ^ { k } \left( \frac { \partial L } { \partial y _ { \alpha } ^ { a }} \circ \sigma ^ { k } \right) ( \frac { \partial } { \partial x } ) ^ { \alpha } ( Z ^ { a } \circ \sigma ) \Delta. \end{equation*}

The problem now is to construct a (horizontal) $n$-form-valued, contact $1$-form $\mathcal{E} ( L )$ on a higher-order jet bundle (as suggested by using integration by parts) so that

\begin{equation*} \sigma ^ { 2 k * } [ {\cal E} ( L ) ( Z ^ { 2 k } ) ] = \sigma ^ { k + 1 * } [ \Omega ( d L \Delta ) ( Z ^ { k + 1 } ) ], \end{equation*}

and so that $\mathcal{E} ( L ) = \mathcal{E} ^ { a } ( L ) \omega ^ { a } \otimes \Delta$, locally on each chart. Consequently, the component expression for the integrand of the first variation is now

\begin{equation*} ( \mathcal{E} ^ { a } ( L ) \circ \sigma ^ { 2 k } ) ( Z ^ { a } \circ \sigma ) \Delta. \end{equation*}

Thus, it follows that if the first variation vanishes identically for all $Z$ of the stated form, then $\sigma$ satisfies $\sigma ^ { 2 k * } \mathcal{E} ( L ) = 0$, which is the global version of the Euler–Lagrange equations. This problem can be solved by using a shift operator $S$.

It is shown in [a1] that there is an operator $S$, called a shift operator, which maps contact-horizontal forms $\phi$ on $E ^ { k + 1 }$ into $n$-forms $S ( \phi )$ on $E ^ { k + 1 }$ (for $k = 0,1 , \ldots$) and which has, on each local chart, the form

\begin{equation*} S ( \phi ) = \sum _ { | \alpha | = 0 } ^ { k - 1 } S _ { \alpha i } ^ { a } ( \phi ) \omega _ { \alpha } ^ { a } \bigwedge \left( \frac { \partial } { \partial x _ { i } } \lrcorner ( d x _ { 1 } \bigwedge \ldots \bigwedge d x _ { n } ) \right). \end{equation*}

By repeated application of $S$ in conjunction with $\Omega$ and $d$, one gets the Euler operator defined in a global way by

\begin{equation*} \mathcal{E} ( L ) \equiv ( 1 + \Omega d S ) ^ { k } \Omega d ( L \Delta ). \end{equation*}

References

[a1]	D. Betounes, "Global shift operators and the higher order calculus of variations" J. Geom. Phys. , 10 (1993) pp. 185–201
[a2]	I. Kolar, "A geometric version of the higher ordered Hamilton formalism in fibered manifolds" J. Geom. Phys. , 1 (1984) pp. 127–137
[a3]	D. Krupka, "Lepagean forms in the higher order variational calculus" , Geometrical Dynamics. Proc. IUTAM–ISIMM Symp. Modern Developments in Analytic. Mech. (Turin, 1982) , I , Technoprint, Bologna (1983) pp. 197–238
[a4]	J. Munoz Masque, "Poincare–Cartan forms in higher order variational calculus on fibered manifolds" Rev. Mat. Iberoamercana , 1 (1985) pp. 85–126
[a5]	D.J. Sanders, "The geometry of jet bundles" , London Math. Soc. Lecture Notes , 142 , Cambridge Univ. Press (1989)