Ellipse
(real)
2020 Mathematics Subject Classification: Primary: 51-XX [MSN][ZBL]
An ellipse is a planar curve obtained by the intersection of a circular cone with a plane not passing through the vertex of the cone and intersecting all its generators in points of one of its sheets. An ellipse also turns out to be the set of points $M$ of a plane (see Figure 1) for each of which the sum of the distances from two given points $F_1$ and $F_2$ (the foci) is constant and equal to $2a > F_1F_2$. The distance between the foci is called the focal distance and is usually denoted by $2c$. The mid-point of the segment $F_1F_2$ is called the centre of the ellipse.
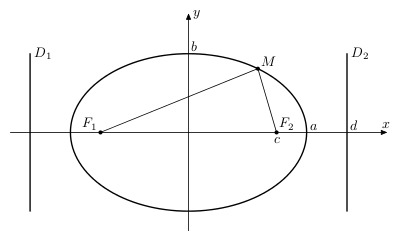
The line on which the foci of the ellipse lie is called the first (or focal) axis. The line through the centre of the ellipse and perpendicular to the first axis is called the second axis. The axes of the ellipse are its axes of symmetry. The points of intersection of the ellipse with the axes of symmetry are called its vertices. The major axis of the ellipse is the segment (and also its length $2a$) of the first axis between the vertices. The minor axis is the segment (and also its length $2b$) of the second axis between the vertices. The number $e = c/a < 1$ is called the eccentricity of the ellipse. A diameter of the ellipse is any straight line passing through the centre; a diameter can also be defined as a straight line passing through the mid-points of parallel chords. The directrix of the ellipse corresponding to a given focus $F$ (the associated directrix) is the line $D$ perpendicular to the first axis at distance $d = a/e$ from the centre. An ellipse has in general two directrices. An ellipse is a central second-order curve with canonical equation $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1. $$ The equation of the tangent to an ellipse at a point $(x_0,y_0)$ is $$ \frac{xx_0}{a^2} + \frac{yy_0}{b^2} = 1. $$
The focal parameter $p$ of an ellipse (half the length of the chord passing through a focus and perpendicular to the first axis) is $b^2/a$. By means of the focal parameter one can write the equation of an ellipse in the form $$ \rho = \frac{p}{1 + e \cos \phi}, $$ where $\rho$ and $\phi$ are polar coordinates, $0 \leq \phi < 2\pi$.
If $a=b$, the ellipse becomes a circle, $F_1 \equiv F_2 \equiv 0$ is its centre, $a$ its radius, $e=0$, and there is no directrix.
An ellipse has the following optical property: A light ray emanating from one focus passes through the other focus after mirror reflection in the ellipse.
A second-order curve with canonical equation $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = -1 $$ where $a$ and $b$ are real numbers, is called an imaginary ellipse.
Comments
As the name suggests, an imaginary ellipse does not have real points.
Other characterizations of an ellipse are as follows.
An ellipse is the affine image of a circle; an ellipse is a non-degenerate conic (i.e. a second-order curve) which does not meet the line at infinity; an ellipse is the set of points whose distances to a given point (the focus) and to a given line (the associated directrix) are in constant ratio; and an ellipse is a planar compact non-singular algebraic curve of the second degree.
For a systematic exposition of the properties of ellipses see [Be], pp. 245–247 and Chapt. 17, and [Co].
References
| [Be] | M. Berger, "Geometry", II, Springer (1987) MR0882541 Zbl 0606.51001 |
| [Co] | J. Coolidge, "A history of the conic sections and quadric surfaces", Dover, reprint (1968) MR0245397 Zbl 0060.01006 |
Ellipse. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ellipse&oldid=25305