Displacement structure

Many problems in engineering and applied mathematics ultimately require the solution of $n \times n$ linear systems of equations. For small-size problems, there is often not much else to do except to use one of the already standard methods of solution, such as Gaussian elimination (cf. also Gauss method). However, in many applications, $n$ can be very large (, ) and, moreover, the linear equations may have to be solved over and over again, with different problem/model parameters, till a satisfactory solution to the original physical problem is obtained. In such cases, the $O ( n ^ { 3 } )$ burden, i.e. the number of flops required to solve an $n \times n$ linear system of equations, can become prohibitively large. This is one reason why one seeks in various classes of applications to identify special/characteristic matrix structures that may be assumed in order to reduce the computational burden.

The most obvious structures are those that involve explicit patterns among the matrix entries, such as Toeplitz, Hankel, Vandermonde, Cauchy, and Pick matrices. Several fast algorithms have been devised over the years to exploit these special structures. However, even more common than these explicit matrix structures are matrices in which the structure is implicit. For example, in certain least-squares problems one often encounters products of Toeplitz matrices; these products are not generally Toeplitz, but, on the other hand, they are not "unstructured" . Similarly, in probabilistic calculations the matrix of interest is often not a Toeplitz matrix, but rather its inverse, which is rarely Toeplitz itself, but of course is not unstructured: its inverse is Toeplitz. It is well-known that $O ( n ^ { 2 } )$ flops suffice to solve linear systems of equations with an $n \times n$ Toeplitz coefficient matrix; a question is whether one will need $O ( n ^ { 3 } )$ flops to invert a non-Toeplitz coefficient matrix whose inverse is known to be Toeplitz? When pressed, one's response clearly must be that it is conceivable that $O ( n ^ { 2 } )$ flops will suffice, and this is in fact true.

Such problems suggest the need for a quantitative way of defining and identifying structure in matrices. Over the years, starting with [a1], it was found that an elegant and useful way to do so is the concept of displacement structure. This concept has also been useful for a host of problems apparently far removed from the solution of linear equations, such as the study of constrained and unconstrained rational interpolation, maximum entropy extension, signal detection, digital filter design, non-linear Riccati differential equations, inverse scattering, certain Fredholm integral equations, etc. (see [a3], [a2] and the many references therein).

For motivation, consider an $n \times n$ Hermitian Toeplitz matrix $T = ( c _ { i - j} ) _ { i , j=0 } ^ { n - 1 } $, $c _ { i } = c _ { - i } ^ { * }$. Since such matrices are completely specified by $n$ entries, rather than $n ^ { 2 }$, one would of course expect a reduction in computational effort for handling problems involving such matrices. However, exploiting the Toeplitz structure is apparently more difficult than it may at first seem. To see this, consider the simple case of a real symmetric $3 \times 3$ Toeplitz matrix and apply the first step of the Gaussian elimination procedure to it, namely

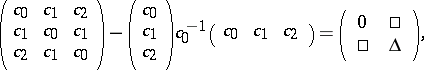where the so-called Schur complement matrix $\Delta$ is seen to be

\begin{equation*} \Delta = \frac { 1 } { c_0 } \left( \begin{array} { c c c } { c_0^ { 2 } - c_ { 1 } ^ { 2 } } & { \square } & { c _ { 1 } c_{0} - c _ { 1 } c _ { 2 } } \\ { c _ { 1 } c _ { 0 } - c _ { 1 } c _ { 2 } } & { \square } & { c _ { 0 } ^ { 2 } - c _ { 2 } ^ { 2 } } \end{array} \right). \end{equation*}

However, $\Delta$ is no longer Toeplitz, so the special structure is lost in the very first step of the procedure. The fact is that what is preserved is not the Toeplitz structure, but a deeper notion called "displacement structure" .

There are several forms of displacement structure, the earliest of which is the following [a1]. Consider an $n \times n$ Hermitian matrix $R$ and the $n \times n$ lower-triangular shift matrix $Z$ with ones on the first subdiagonal and zeros elsewhere (i.e., a lower-triangular Jordan block with eigenvalues at $0$). The displacement of $R$ with respect to $Z$, denoted by $\nabla _ { Z } R$, is defined as the difference

\begin{equation*} \nabla _ { Z } R = R - Z R Z ^ { * }. \end{equation*}

The matrix $R$ is said to have displacement structure (or to be of low displacement rank) with respect to $Z$ if the rank of $\nabla _ { Z } R$ is considerably lower than (and independent of) $n$. For example, a Hermitian Toeplitz matrix has displacement rank $2$ with respect to $Z$.

More generally, let $r \ll n$ denote the rank of $\nabla _ { Z } R$. Then one can write $\nabla _ { Z } R$ as $\nabla _ { Z } R = G J G ^ { * }$, where $G$ is an $( n \times r )$-matrix and $J$ is a "signature" matrix of the form $J = ( I _ { p } \oplus - l _ { q } )$ with $p + q = r$. This representation is highly non-unique, since $G$ can be replaced by $G \Theta$ for any $J$-unitary matrix $\Theta$, i.e. for any $\Theta$ such that $\Theta J \Theta ^ { * } = J$; this flexibility is actually very useful. The matrix $G$ is said to be a generator matrix for $R$ since, along with $\{ Z , J \}$, it completely identifies $R$. If one labels the columns of $G$ as

\begin{equation*} G = \left( \begin{array} { c c c c c c c } { x _ { 0 } } & { \square \ldots \square} & { x _ { p - 1 } } & { y _ { 0 } } & { \square \ldots \square } & { y _ { q - 1 } } \end{array} \right), \end{equation*}

and lets $L ( x )$ denote a lower-triangular Toeplitz matrix whose first column is $x$, then it can be seen that the unique $R$ that solves the displacement equation $\nabla _ { Z } R = G J G ^ { * }$ is given by

\begin{equation*} R = \sum _ { i = 0 } ^ { n - 1 } Z ^ { i } G J G ^ { * } Z ^ { * i } = \end{equation*}

\begin{equation*} = \sum _ { i = 0 } ^ { p - 1 } L ( x _ { i } ) L ^ { * } ( x _ { i } ) - \sum _ { i = 0 } ^ { q - 1 } L ( y _ { i } ) L ^ { * } ( y _ { i } ). \end{equation*}

Such displacement representations of $R$ as a combination of products of lower- and upper-triangular Toeplitz matrices allow, for example, bilinear forms such as $x ^ { * } R y$ to be rapidly evaluated via convolutions (and hence fast Fourier transforms).

As mentioned above, a general Toeplitz matrix has displacement rank $2$, with in fact $p = 1$ and $q = 1$. But there are interesting non-Toeplitz matrices with $p = 1 = q$, for example the inverse of a Toeplitz matrix. In fact, this is a special case of the following fundamental result: If $R$ is invertible and satisfies $R - Z R Z ^ { * } = G J G ^ { * }$, then there exists a $\widetilde { H }$ such that $R ^ { - 1 } - Z ^ { * } R ^ { - 1 } Z = \widetilde{ H } \square ^ { * } J \widetilde { H }$. The fact that $Z$ and $ Z ^ { * }$ are interchanged in the latter formula suggests that one can define a so-called "natural" inverse, $R ^ { - \# } = \tilde{I} R ^ { - 1 } \tilde{I}$, where $\tilde{I}$ is the "reverse" identity matrix (with ones on the anti-diagonal). For then one sees (with $H = \tilde{I} \tilde { H } \square ^{*}$) that

\begin{equation*} R ^ { - \# } - Z R ^ { - \# } Z ^ { * } = H J H ^ { * }. \end{equation*}

Therefore, $R$ and $R ^ { - \# }$ have the same displacement rank and (when $R$ is Hermitian) the same displacement inertia (since $J$ is the same). (A real symmetric Toeplitz matrix $T$ has $T ^ { - 1 } = T ^ { - \# }$, so that $T ^ { - 1 }$ has a representation of the form $T ^ { - 1 } = L ( x ) L ^ { * } ( x ) - L ( y ) L ^ { * } ( y )$, which after suitably identifying $\{ x , y \}$ is a special so-called Gohberg–Semencul formula.) The proof of the above fundamental result is very simple (see, e.g., [a3]) and in fact holds with $Z$ replaced by any matrix $F$.

An interesting example is obtained by choosing $F = \operatorname { diag } \{ f _ { 0 } , \dots , f _ { n - 1 } \}$, $| f _ { i } | < 1$, when the solution $R$ of the displacement equation $R - F R F ^ { * } = G J G ^ { * }$ becomes a "Pick" matrix of the form

\begin{equation*} P = \left( \frac { u _ { i } u _ { j } ^ { * } - v _ { i } v _ { j } ^ { * } } { 1 - f _ { i } f _ { j } ^ { * } } \right) _ { i , j = 0 } ^ { n - 1 }, \end{equation*}

where $\{ u_ { i } , v _ { i } \}$ are $1 \times p$ and $1 \times q$ vectors. Pick matrices arise in solving analytic interpolation problems and the displacement theory gives new and efficient computational algorithms for solving a variety of such problems (see, e.g., [a2] and Nevanlinna–Pick interpolation).

One can handle non-Hermitian structured matrices by using displacement operators of the form $\nabla _ { F, A} R = R - F R A ^ { * }$. When $F$ is diagonal with distinct entries and $A = Z$, $R$ becomes a Vandermonde matrix. A closely related displacement operator, first introduced in [a4], has the form $F R - R A ^ { * }$. Choosing $F = \operatorname { diag } \{ f _ { i } \}$, $A = \operatorname { diag } \{ a _ { i } \}$ leads to Cauchy-like solutions of the form

\begin{equation*} C _ { l } = \left( \frac { u _ { i } v _ { j } ^ { * } } { f _ { i } - a _ { j } ^ { * } } \right) , u _ { i } , v _ { i } \in \mathcal C ^ { 1 \times r }. \end{equation*}

The name comes from the fact that when $r = 1$ and $u _ { 0 } = 1 = v _ { 0 }$, $C_l$ is a Cauchy matrix. When $r = 2$, and $u _ { i } = \left( \beta _ { i } \quad 1 \right) $ and $v _ { i } = ( 1 - k _ { i } )$, one gets the so-called Loewner matrix.

It is often convenient to use generating-function language, and to define

\begin{equation*} R ( z , w ) = \sum _ { i , j = 0 } ^ { \infty } R _ { ij } z ^ { i } w ^ { * j }. \end{equation*}

(Finite structured matrices can be extended to be semi-infinite in many natural ways, e.g. by extending the generator matrix by adding additional rows.) In this language, one can introduce general displacement equations of the form

\begin{equation*} d ( z , w ) R ( z , w ) = G ( z ) J G ^ { * } ( w ), \end{equation*}

with

\begin{equation*} d ( z , w ) = \sum _ { i , j = 0 } ^ { \infty } d _ { i j } z ^ { i } w ^ { * j }. \end{equation*}

Choosing $d ( z , w ) = 1 - z w ^ { * }$ corresponds to matrix displacement equations of the form (in an obvious notation), $R - Z R Z ^ { * } = G J G ^ { * }$, while $d ( z , w ) = ( z - w ^ { * } )$ corresponds to $Z R - R Z ^ { * } = G J G ^ { * }$. There are many other useful choices, but to enable recursive matrix factorizations it is necessary to restrict $d ( z , w )$ to the form $d ( z , w ) = \alpha ( z ) \alpha ^ { * } ( w ) - \beta ( z ) \beta ^ { * } ( w )$. Note, in particular, that for $R = I$ one gets $R ( z , w ) = 1 / ( 1 - z w ^ { * } )$, the Szegö kernel. Other choices lead to the various so-called de Branges and Bergman kernels. See [a5] and the references therein.

A central feature in many of the applications mentioned earlier is the ability to efficiently obtain the so-called triangular LDU-factorization of a matrix and of its inverse (cf. also Matrix factorization). Among purely matrix computations, one may mention that this enables fast determination of the so-called QR-decomposition and the factorization of composite matrices such as $T _ { 1 } T _ { 2 } ^ { - 1 } T _ { 3 }$, $T _ { i }$ being Toeplitz. The LDU-factorization of structured matrices is facilitated by the fact that Schur complements inherit displacement structure. For example, writing

\begin{equation*} R = \left( \begin{array} { l l } { R _ { 11 } } & { R _ { 12 } } \\ { R _ { 21 } } & { R _ { 22 } } \end{array} \right), F = \left( \begin{array} { l l } { F _ { 1 } } & { 0 } \\ { F _ { 2 } } & { F _ { 3 } } \end{array} \right), \end{equation*}

it turns out that

\begin{equation*} \operatorname { rank } ( S - F _ { 3 } S F _ { 3 } ^ { * } ) \leq \operatorname { rank } ( R - F R F ^ { * } ), \end{equation*}

where $S = R _ { 22 } - R _ { 21 } R _ { 11 } ^ { - 1 } R _ { 12 }$. By properly defining the $\{ R_{ij} \}$ and $\{ F _ { i } \}$, this allows one to find the displacement structure of various composite matrices. For example, choosing $R _ { 11 } = - T$, $R _ { 12 } = I = R _ { 21 }$, $R _ { 22 } = 0$, and $F = Z \oplus Z$, gives the previously mentioned result on inverses of structured matrices.

Computations on structured matrices are made efficient by working not with the $n ^ { 2 }$ entries of $R$, but with the $n r$ entries of the generator matrix $G$. The basic triangular factorization algorithm is Gaussian elimination, which, as noted in the first calculation, amounts to finding a sequence of Schur complements. Incorporating structure into the Gaussian elimination procedure was, in retrospect, first done (in the special case $r = 2$) by I. Schur himself in a remarkable 1917 paper dealing with the apparently very different problem of checking when a power series is bounded in the unit disc.

The algorithm below is but one generalization of Schur's original recursion. It provides an efficient $O ( m ^ { 2 } )$ procedure for the computation of the triangular factors of a Hermitian positive-definite matrix $R$ satisfying

\begin{equation*} R - Z R Z ^ { * } = G J G ^ { * } , G \in \mathcal{C} ^ { n \times r }, \end{equation*}

with $J = ( I _ { p } \oplus - l _ { q } )$. So, let $R = L D ^ { - 1 } L ^ { * }$ denote the triangular decomposition of $R$, where $D = \operatorname { diag } \{ d _ { 0 } , \dots , d _ { n - 1 } \}$, and the lower triangular factor $L$ is normalized in such a way that the $\{ d _ { i } \}$ appear on its main diagonal. The non-zero part of the consecutive columns of $L$ will be further denoted by $l_i$. Then it holds that the successive Schur complements of $R$ with respect to its leading $( i \times i )$-submatrices, denoted by $R_i$, are also structured and satisfy

\begin{equation*} R _ { i } - Z _ { i } R _ { i } Z _ { i } ^ { * } = G _ { i } J G _ { i } ^ { * }, \end{equation*}

with $( n - i ) \times ( n - i )$ lower-triangular shift matrices $Z_{i}$, and where the generator matrices $G_i$ are obtained by the following recursive construction:

start with $G _ { 0 } = G$;

repeat for $i \geq 0$:

\begin{equation*} \left( \begin{array} { c } { 0 } \\ { G _ { i + 1 } } \end{array} \right) = \left\{ G _ { i } + Z _ { i } G _ { i } \frac { J g _ { i } ^ { * } g _ { i } } { g _ { i } J g _ { i } ^ { * } } \right\} \Theta _ { i }, \end{equation*}

where $\Theta_i$ is an arbitrary $J$-unitary matrix, and $g_i$ denotes the top row of $G_i$. Then

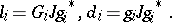The degree of freedom in choosing $\Theta_i$ is often very useful. One particular choice leads to the so-called proper form of the generator recursion. Let $\Theta_i$ reduce $g_i$ to the form

\begin{equation*} g _ { i } \Theta _ { i } = \left( \begin{array} { l l l } { \delta _ { i } } & { 0 } & { \ldots } & { 0 } \end{array} \right), \end{equation*}

with a non-zero scalar entry in the leading position. Then

\begin{equation*} \left( \begin{array} { c } { 0 } \\ { G _ { i + 1 } } \end{array} \right) = Z _ { i } G _ { i } \Theta _ { i } \left( \begin{array} { c c } { 1 } & { 0 } \\ { 0 } & { 0 } \end{array} \right) + G _ { i } \Theta _ { i } \left( \begin{array} { c c } { 0 } & { 0 } \\ { 0 } & { I _ { p + q - 1 } } \end{array} \right), \end{equation*}

with

\begin{equation*} l _ { i } = \delta _ { i } ^ { * } G _ { i } \Theta _ { i } \left( \begin{array} { c } { 1 } \\ { 0 } \end{array} \right) , d _ { i } = | \delta _ { i } | ^ { 2 }. \end{equation*}

In words, this shows that $G _ { i+1 } $ can be obtained from $G_i$ as follows:

1) reduce $g_i$ to proper form;

2) multiply $G_i$ by $\Theta_i$ and keep the last columns of $ { G } _ { i } \Theta _ { i }$ unaltered;

3) shift down the first column of $ { G } _ { i } \Theta _ { i }$ by one position.

Extensions of the algorithm to more general structured matrices are possible (see, e.g., [a2], [a3]). In addition, the algorithm can be extended to provide simultaneous factorizations of both a matrix $R$ and its inverse, $R ^ { - 1 }$; see, e.g., [a3].

An issue that arises in the study of such fast factorization algorithms is their numerical stability in finite-precision implementations. It was mentioned earlier that the generalized Schur algorithm amounts to combining Gaussian elimination with structure, and it is well-known that Gaussian elimination in its purest form is numerically unstable (meaning that the error in the factorization 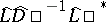can be quite large, where $\hat{L}$ and $\hat{D}$ denote the computed $L$ and $D$, respectively). The instability can often be controlled by resorting to pivoting techniques, i.e., by permuting the order of the rows, and perhaps columns, of the matrices before the Gaussian elimination steps. However, pivoting can destroy matrix structure and can thus lead to a loss in computational efficiency. It was observed in [a6], though, that for diagonal displacement operators $F$, and more specifically for Cauchy-like matrices, partial pivoting does not destroy matrix structure. This fact was exploited in [a7] in the context of the generalized Schur algorithm and applied to other structured matrices. This was achieved by showing how to transform different kinds of matrix structure into Cauchy-like structure.

Partial pivoting by itself is not sufficient to guarantee numerical stability even for slow algorithms. Moreover, the above transformation-and-pivoting technique is only efficient for fixed-order problems, since the transformations have to be repeated afresh whenever the order changes. Another approach to the numerical stability of the generalized Schur algorithm is to examine the steps of the algorithm directly and to stabilize them without resorting to transformations among matrix structures. This was done in [a8], where it was shown, in particular, how to implement the hyperbolic rotations in a reliable manner. For all practical purposes, the main conclusion of [a8] is that the generalized Schur algorithm, with certain modifications, is backward stable for a large class of structured matrices.

References

[a1]	T. Kailath, S.Y. Kung, M. Morf, "Displacement ranks of a matrix" Bull. Amer. Math. Soc. , 1 : 5 (1979) pp. 769–773
[a2]	T. Kailath, A.H. Sayed, "Displacement structure: Theory and applications" SIAM Review , 37 (1995) pp. 297–386
[a3]	T. Kailath, "Displacement structure and array algorithms" T. Kailath (ed.) A.H. Sayed (ed.) , Fast Reliable Algorithms for Matrices with Structure , SIAM (Soc. Industrial Applied Math.) (1999)
[a4]	G. Heinig, K. Rost, "Algebraic methods for Toeplitz-like matrices and operators" , Akad. (1984)
[a5]	H. Lev-Ari, T. Kailath, "Triangular factorization of structured Hermitian matrices" I. Gohberg (ed.) et al. (ed.) , Schur Methods in Operator Theory and Signal Processing , Birkhäuser (1986) pp. 301–324
[a6]	G. Heinig, "Inversion of generalized Cauchy matrices and other classes of structured matrices" A. Bojanczyk (ed.) G. Cybenko (ed.) , Linear Algebra for Signal Processing , IMA volumes in Mathematics and its Applications , 69 (1994) pp. 95–114
[a7]	I. Gohberg, T. Kailath, V. Olshevsky, "Fast Gaussian elimination with partial pivoting for matrices with displacement structure" Math. Comput. , 64 (1995) pp. 1557–1576
[a8]	S. Chandrasekaran, A.H. Sayed, "Stabilizing the generalized Schur algorithm" SIAM J. Matrix Anal. Appl. , 17 (1996) pp. 950–983