Density hypothesis
A proposed inequality providing a bound for the number $ N( \sigma , T) $
of zeros $ \rho = \beta + i \gamma $
of the Riemann zeta-function
$$ \zeta ( s) = \sum _ {n=1} ^ \infty \frac{1}{n ^ {s} } , $$
where $ s = \sigma + it $, in the rectangle $ 1/2< \sigma \leq \beta \leq 1 $, $ | \gamma | \leq T $.
The most exact formulation of the density hypothesis is
$$ N( \sigma , T) \leq cT ^ {2( 1- \sigma ) } \mathop{\rm ln} ^ {A} T. $$
A simpler, but less accurate, form of the density hypothesis is
$$ N( \sigma , T) \leq cT ^ {2( 1- \sigma )+ \epsilon } . $$
The density hypothesis enables one to obtain results in the theory of prime numbers that are comparable with those following from the Riemann hypothesis. For example, it follows from the density hypothesis that for sufficiently large $ x $ there is at least one prime number in each segment $ [ x, x+ x ^ {\epsilon + 1/2 } ] $.
The density hypothesis is a consequence of the stronger Lindelöf hypothesis. A difference from the latter is that the density hypothesis has been partially proved, in terms of various density theorems, beginning with certain values $ \sigma \geq \sigma _ {0} > 1/2 $.
For the number $N(\sigma, T, \chi)$ of zeros of Dirichlet $L$-functions
$$ L( s, \chi ) = \sum _ {n=1} ^ \infty \frac{\chi ( n, k) }{n ^ {s} } , $$
where $ \chi ( n, k) $ is a character modulo $ k $, an analogous density hypothesis is posed. In averaged form, this is
$$ \tag{1 } \sum _ {\chi \mathop{\rm mod} k } N( \sigma , T, \chi ) \leq c( kT) ^ {2( 1- \sigma )+ \epsilon } , $$
$$ \tag{2 } \sum _ {k\leq Q } \sum _ {\chi ^ {*} \mathop{\rm mod} k } N( \sigma , T, \chi ^ {*} ) \leq c( k ^ {2} T) ^ {2( 1- \sigma )+ \epsilon } , $$
where $ \chi ^ {*} $ is a primitive character modulo $ k $.
The density hypothesis for Dirichlet $ L $ functions is used in the theory of the distribution of prime numbers belonging to arithmetic progressions.
References
| [1] | H. Davenport, "Multiplicative number theory" , Springer (1980) |
| [2] | A.F. Lavrik, "A survey of Linnik's large sieve and the density theory of zeros of 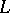 -functions" Russian Math. Surveys , 35 : 2 (1980) pp. 63–76 Uspekhi Mat. Nauk , 35 : 2 (1980) pp. 55–65 -functions" Russian Math. Surveys , 35 : 2 (1980) pp. 63–76 Uspekhi Mat. Nauk , 35 : 2 (1980) pp. 55–65 |
Comments
For extra references see also Density method. Cf. also Distribution of prime numbers.
Let $ N _ {2} $ be the double sum in (2) above. Then the estimates of A.I. Vinogradov [a1], [a2] and E. Bombieri [a3] (the Bombieri–Vinogradov theorem) are, respectively,
$$ N _ {2} \ll \ k ^ {3 - 2 \sigma + \epsilon } ( T \mathop{\rm log} k) ^ {c _ {0} \epsilon ^ {-} 4 } $$
and
$$ N _ {2} \ll \ T ( k ^ {2} + kT) ^ {4 ( 3 - 2 \sigma ) ^ {-} 1 ( 1 - \sigma ) } \ \mathop{\rm log} ^ {10} ( kT). $$
Let $ N _ {1} $ be the sum in (1) above. More recent results on $ N _ {1} $ and $ N _ {2} $ for, respectively, $ 1/2 \leq \sigma \leq 3/4 $, $ 3/4 \leq \sigma \leq 4/5 $ and $ 4/5 \leq \sigma \leq 1 $ are due to H.L. Montgomery, M.N. Huxley, and M. Jutila and are, respectively (cf. [2]),
$$ N _ {1} \ll ( kT) ^ {3 ( 2 - \sigma ) ^ {-} 1 ( 1 - \sigma ) } \ \mathop{\rm log} ^ {9} ( kT),\ \ \frac{1}{2} \leq \sigma \leq \frac{3}{4} , $$
$$ N _ {1} \ll ( kT) ^ {3 ( 3 \sigma - 1) ^ {-} 1 ( 1 - \sigma ) + \epsilon } ,\ \frac{3}{4} \leq \sigma \leq \frac{4}{5} , $$
$$ N _ {1} \ll ( kT) ^ {( 2 + \epsilon ) ( 1 - \sigma ) } ,\ \frac{4}{5} \leq \sigma \leq 1 , $$
and for $ N _ {2} $,
$$ N _ {2} \ll ( k ^ {2} T) ^ {3 ( 2 - \sigma ) ^ {-} 1 ( 1 - \sigma ) } \ \mathop{\rm log} ^ {14} ( kT) ,\ \ \frac{1}{2} \leq \sigma \leq \frac{3}{4} , $$
$$ N _ {2} \ll ( k ^ {2} T) ^ {3 ( 3 \sigma - 1) ^ {-} 1 ( 1 - \sigma ) + \epsilon } ,\ \frac{3}{4} \leq \sigma \leq \frac{4}{5} , $$
$$ N _ {2} \ll ( k ^ {2} T) ,\ \frac{4}{5} \leq \sigma \leq 1 . $$
References
| [a1] | A.I. Vinogradov, "The density hypothesis for Dirichlet L-series" Izv. Akad. Nauk SSSR Ser. Mat. , 29 (1965) pp. 903–934 (In Russian) |
| [a2] | A.I. Vinogradov, "Correction to "The density hypothesis for Dirichlet L-series" " Izv. Akad. Nauk SSSR Ser. Mat. , 30 (1966) pp. 719–720 (In Russian) |
| [a3] | E. Bombieri, "On the large sieve" Mathematika , 12 (1965) pp. 201–225 |
Density hypothesis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Density_hypothesis&oldid=54848