Collapsibility
of a triangulation
Originally, a property of simplicial complexes (cf. Simplicial complex), extending naturally to simplicial sets (cf. Simplicial set) and cell complexes (cf. Cell complex). For a pair $ X \supset Y $ of polyhedra or complexes (see Polyhedron, abstract), one says there is an elementary collapse of $ X $ on $ Y $, and writes $ X \searrow ^ {e} Y $, if $ X $ is the union of $ Y $ with precisely two more simplexes $ e ^ {n} $, $ e ^ {n - 1 } $, one a maximal face of the other. $ X $ collapses on $ Y $ if there is a sequence, possibly transfinite, of elementary collapses
$$ X = X _ {0} \searrow ^ {e} X _ {1} \searrow ^ {e} \dots \searrow ^ {e} X _ \alpha = Y. $$
Here, $ X _ \lambda $ for a limit ordinal $ \lambda $ must be the intersection of the preceding $ X _ \kappa $. Then $ Y $ is called a spine of $ X $, and one writes $ X \searrow Y $. If $ X $ collapses to a point, one says that $ X $ is collapsible and writes $ X \searrow 0 $.
Collapses were first introduced [a18] for two applications which are fundamental for piecewise-linear topology: description of the internal structure of a complex, and the definition of simple homotopy type. The "modern" , functorial, definition is (see Simple homotopy type) that two complexes $ X $, $ Y $ have the same simple homotopy type if there exists a homotopy equivalence $ \theta : X \rightarrow Y $ with zero Whitehead torsion. This is equivalent to Whitehead's constructive definition: $ X $ and $ Y $ can be joined by a "zigzag" chain of collapses
$$ X = X _ {0} \searrow X _ {1} \swarrow X _ {2} \searrow \dots \searrow X _ {k} = Y $$
(for finite complexes; it can be extended to infinite complexes). It was clear at once that collapsible complexes (and the underlying (piecewise-linear) polyhedra and topological polyhedra) are an interesting class of spaces: the best behaved contractible polyhedra. Every $ 1 $- dimensional contractible complex (topological tree) is collapsible. However, there are simple examples of contractible but not collapsible $ 2 $- dimensional complexes, such as the house with two rooms [a4] and the dunce hat [a19].
The centre of interest in collapsible polyhedra is the Zeeman conjecture, stating that for every contractible $ 2 $- dimensional complex $ K $, $ K \times I $ is collapsible. This was proposed by E.C. Zeeman [a19], who showed that it implies the Poincaré conjecture. Nearly twenty years later, D. Gillman and D. Rolfsen showed [a7] that the conjectures are equivalent, at least if the Zeeman conjecture is somewhat restricted, as explained below. This equivalence has the happy effect of "blowing-up" the problem into something that has parts, unlike the original Poincaré conjecture, which merely says that certain spaces cannot exist. Indeed, another part of Zeeman's conjecture has been shown [a13] to be equivalent to a conjecture of J.J. Andrews and M.L. Curtis [a1] on contractible $ 2 $- dimensional complexes, which acquires much greater interest because of its equivalence in turn with a major conjecture in combinatorial group theory. These things are explained below.
Note that there is another field in which collapsibility is prominent, and which is less dependent upon conjecture. It revolves around the question: What are the topological types of injective or hyperconvex metric spaces? (See Metric space.) N. Aronszajn and P. Panitchpakdi speculated [a3] that they might be just the (metrizable) AR's (see Retract of a topological space); and for $ 1 $- dimensional spaces it is true [a16]. However, J. Isbell showed [a10] that a compact $ 2 $- dimensional polyhedron underlies an injective metric space if and only if it underlies a collapsible complex, and observed that this might extend to higher dimensions. At least half of it does, in that finite collapsible complexes are homeomorphic with injective metric spaces [a11].
Why is the Zeeman conjecture restricted to $ 2 $- dimensional contractible complexes? Zeeman did not say, but soon there was speculation about an extended Zeeman conjecture in high dimensions. M. Cohen showed in 1977 [a6] that that is false beyond dimension $ 2 $.
Another point around the boundary of the Zeeman conjecture is as follows. Of course, contractibility is a topological property, while collapsibility is not. Nevertheless, it may well be true that for every triangulation of a contractible $ 2 $- dimensional polyhedron $ K $, $ K \times I $ is collapsible (the full Zeeman conjecture). In this connection it is easy to show that for $ 2 $- dimensional polyhedra, collapsibility is a topological invariant. In fact, for compact $ 2 $- dimensional polyhedra it is equivalent [a10] to topological collapsibility (defined below). For $ 3 $- dimensional polyhedra, even the $ 3 $- dimensional ball, collapsibility depends on the triangulation [a8].
Here is a very rough sketch of Zeeman's proof that his conjecture implies Poincaré's. Given a fake $ 3 $- dimensional sphere (a simply connected closed $ 3 $- dimensional manifold) $ M $, remove an open piecewise-linear 3-dimensional ball $ B $. Then $ M \setminus B $ collapses to a $ 2 $- dimensional complex $ K $ which is easily shown to be contractible. So, given the Zeeman conjecture, $ ( M \setminus B ) \times I \searrow K \times I \searrow 0 $. By a classical theorem of J.H.C. Whitehead (see [a17]) this makes $ ( M \setminus B ) \times I $ a piecewise-linear $ 4 $- dimensional ball, and the rest is easy.
It is known that the Poincaré conjecture is equivalent to the Zeeman conjecture restricted to special spines (of $ 3 $- dimensional manifolds with boundary). Special (also standard) polyhedra are compact $ 2 $- dimensional polyhedra $ K $ having a piecewise-linear CW-decomposition whose $ j $- skeletons $ K ^ {j} $ are topologically defined as follows. $ K ^ {2} $ is the set of points where $ K $ is locally $ \mathbf R ^ {2} $; $ K ^ {1} $ is the set in $ K \setminus K ^ {2} $ where $ K $ is locally three half-planes with a common edge; $ K ^ {0} $ is the remainder, where $ K $ must be locally four trihedral angles sharing six face angles in pairs. Every connected $ 3 $- dimensional manifold with boundary has a special spine [a5].
The original Andrews–Curtis conjecture [a1] concerns balanced presentations of the $ 1 $- element group, i.e., presentations by $ r $ generators $ a _ {i} $ and $ r $ relations $ R _ {i} $. It states that every such presentation can be reduced to the trivial presentation in which $ R _ {i} = a _ {i} $ by transformations of four types, three from J. Nielsen's 1919 paper [a14] and, fourth, replacing a relation $ R _ {i} $ with $ wR _ {i} w ^ {- 1 } $ for any word $ w $. (See the expository paper [a2].) A number of equivalent propositions are known [a9]. The basic topological one is that each $ 2 $- dimensional contractible complex can be joined to a point by a zigzag chain of collapses, all within $ 3 $- dimensional complexes. (If one replaces "2" and "3" by "n" and ` "n+ 1" , with $ n > 2 $, this is a theorem of Whitehead [a19].) As for the Zeeman conjecture, its specialization to contractible special polyhedra which are not imbeddable in any $ 3 $- dimensional manifold is equivalent to the Andrews–Curtis conjecture [a13].
Topological collapsibility [a15] is the existence of a free contraction to a point, i.e., a homotopy $ \{ h _ {t} \} $ with $ h _ {1} ( x ) = x $, $ h _ {0} ( x ) = \textrm{ const } $, and for all $ s,t $ $ h _ {s} h _ {t} = h _ { \min \{ s,t \} } $. For compact polyhedra, collapsibility implies injectivity [a11] and injectivity implies topological collapsibility [a10]. There seems to be no known example (1996) of a topologically collapsible polyhedron which has no collapsible triangulation.
References
| [a1] | J.J. Andrews, M.L. Curtis, "Free groups and handlebodies" Proc. Amer. Math. Soc. , 16 (1965) pp. 192–195 |
| [a2] | J.J. Andrews, M.L. Curtis, "Extended Nielsen operations in free groups" Amer. Math. Monthly , 73 (1966) pp. 21–28 |
| [a3] | N. Aronszajn, P. Panitchpakdi, "Extension of uniformly continuous transformations and hyperconvex metric spaces" Pacific J. Math. , 6 (1956) pp. 405–439 |
| [a4] | R.H. Bing, "Some aspects of the topology of 3-manifolds related to the Poincaré conjecture" , Lectures on Modern Mathematics , II , Wiley (1964) pp. 93–128 |
| [a5] | B.G. Casler, "An imbedding theorem for connected 3-manifolds with boundary" Proc. Amer. Math. Soc. , 16 (1965) pp. 559–566 |
| [a6] | M.M. Cohen, "Whitehead torsion, group extensions, and Zeeman's conjecture in high dimensions" Topology , 16 (1977) pp. 79–88 |
| [a7] | D. Gillman, D. Rolfsen, "The Zeeman conjecture for standard spines is equivalent to the Poincaré conjecture" Topology , 22 (1983) pp. 315–323 |
| [a8] | R.E. Goodrick, "Non-simplicially collapsible triangulations of 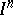 " Proc. Cambridge Philos. Soc. , 64 (1968) pp. 31–36 " Proc. Cambridge Philos. Soc. , 64 (1968) pp. 31–36 |
| [a9] | "Two-dimensional homotopy and combinatorial group theory" C. Hog-Angeloni (ed.) W. Metzler (ed.) A. Sieradski (ed.) , Lecture Notes , 197 , Cambridge Univ. Press (1993) |
| [a10] | J.R. Isbell, "Six theorems about injective metric spaces" Comment. Math. Helv. , 39 (1964) pp. 65–76 |
| [a11] | J. Mai, Y. Tang, "An injective metrization for collapsible polyhedra" Proc. Amer. Math. Soc. , 88 (1983) pp. 333–337 |
| [a12] | J. Mai, Y. Tang, "On the injective metrization for infinite collapsible polyhedra" Acta Math. Sinica (N.S.) , 7 (1991) pp. 13–18 |
| [a13] | S.V. Matveev, "The Zeeman conjecture for non-thickenable special polyhedra is equivalent to the Andrews–Curtis conjecture" Siberian Math. J. , 28 (1987) pp. 917–928 Sibirsk. Mat. Zh. , 28 (1987) pp. 66–80;218 |
| [a14] | J. Nielsen, "Über die Isomorphismen unendlicher Gruppen ohne Relation" Math. Ann. , 79 (1919) pp. 269–272 |
| [a15] | R. Piergallini, "Topological collapsing and cylindrical neighborhoods in  -manifolds" Topology Appl. , 20 (1985) pp. 257–278 -manifolds" Topology Appl. , 20 (1985) pp. 257–278 |
| [a16] | R.L. Plunkett, "Concerning two types of convexity for metrics" Arch. Math. , 10 (1959) pp. 42–45 |
| [a17] | C.P. Rourke, B.J. Sanderson, "Introduction to piecewise-linear topology" , Springer (1972) |
| [a18] | J.H.C. Whitehead, "Simplicial spaces, nuclei and 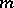 -groups" Proc. London Math. Soc. , 45 (1939) pp. 243–327 -groups" Proc. London Math. Soc. , 45 (1939) pp. 243–327 |
| [a19] | E.C. Zeeman, "On the dunce's hat" Topology , 2 (1964) pp. 341–358 |
Collapsibility. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Collapsibility&oldid=53370