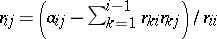Cholesky factorization
A symmetric $( n \times n )$ matrix $A$ (cf. also Symmetric matrix) is positive definite if the quadratic form $x ^ { T } A x$ is positive for all non-zero vectors $x$ or, equivalently, if all the eigenvalues of $A$ are positive. Positive-definite matrices have many important properties, not least that they can be expressed in the form $A = X ^ { T } X$ for a non-singular matrix $X$. The Cholesky factorization is a particular form of this factorization in which $X$ is upper triangular with positive diagonal elements, and it is usually written as $A = R ^ { T } R$. In the case of a scalar ($n = 1$), Cholesky factorization corresponds to the fact that a positive number has a positive square root. The factorization is named after A.-L. Cholesky, a French military officer involved in geodesy. It is closely connected with the solution of least-squares problems (cf. also Least squares, method of), since the normal equations that characterize the least-squares solution have a symmetric positive-definite coefficient matrix.
The Cholesky factorization can be computed by a form of Gaussian elimination that takes advantage of the symmetry and definiteness. Equating $( i , j )$ elements in the equation $A = R ^ { T } R$ gives
\begin{equation*} j = i :\, a _ { i i } = \sum _ { k = 1 } ^ { i } r _ { k i } ^ { 2 }, \end{equation*}
\begin{equation*} j > i : a _ { ij } = \sum _ { k = 1 } ^ { i } r _ { k i } r _ { k j }. \end{equation*}
These equations can be solved to yield $R$ a column at a time, according to the following algorithm:
|
It is the positive definiteness of $A$ that guarantees that the argument of the square root in this algorithm is always positive.
It can be shown [a1] that in floating-point arithmetic the computed solution $\hat{x}$ satisfies $( A + \Delta A ) \hat{x} = b$, where $\| \Delta A \| _ { 2 } \leq c n ^ { 2 } u \| A \| _ { 2 }$, with $c$ a constant of order $1$ and $u$ the unit round-off (or machine precision). Here, $\|A \| _ { 2 } = \operatorname { max } _ { x \neq 0} \|Ax\|_2 / \| x \|_2$ and $\| x \| _ { 2 } = ( x ^ { T } x ) ^ { 1 / 2 }$. This excellent numerical stability is essentially due to the equality $\| A \| _ { 2 } = \| R ^ { T } R \| _ { 2 } = \| R \| _ { 2 } ^ { 2 }$, which guarantees that $R$ is of bounded norm relative to $A$.
A variant of Cholesky factorization is the factorization $A = L D L ^ { T }$ where $L$ is unit lower triangular and $D$ is diagonal. This factorization exists for definite matrices and some (but not all) indefinite ones. When $A$ is positive definite, the Cholesky factor is given by $R = D ^ { 1 / 2 } L ^ { T }$.
A symmetric matrix $A$ is positive semi-definite if the quadratic form $x ^ { T } A x$ is non-negative for all $x$; thus, $A$ may be singular (cf. also Matrix). For such matrices a Cholesky factorization exists, but $R$ may not display the rank of $A$. However, by introducing row and column permutations it is always possible to obtain a factorization
\begin{equation*} \Pi ^ { T } A \Pi = R ^ { T } R , \quad R = \left( \begin{array} { c c } { R _ { 11 } } & { R _ { 12 } } \\ { 0 } & { 0 } \end{array} \right), \end{equation*}
where $\Pi$ is a permutation matrix, $R _ { 11 }$ is $( r \times r )$ upper triangular with positive diagonal elements, and $\operatorname {rank} ( A ) = r$.
Cf. Matrix factorization for more details and references.
References
| [a1] | N.J. Higham, "Accuracy and stability of numerical algorithms" , SIAM (Soc. Industrial Applied Math.) (1996) |
Cholesky factorization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cholesky_factorization&oldid=56214