Braided group

braided Hopf algebra, braided bi-algebra

A Hopf algebra, or bi-algebra, in a braided category. In physical terms, this is a generalization of both the notion of a quantum group (cf. also Quantum groups) and a super-group, in which the role of Bose–Fermi statistics is now played by more general braid statistics. The term is sometimes also used (incorrectly) for an ordinary Hopf algebra equipped with a (co-) quasi-triangular structure, see Quasi-triangular Hopf algebra.

Associated to braided groups is a new "three-dimensional" kind of algebra, in which the algebraic information is expressed by braid and knot diagrams. In effect, algebraic operations are implemented by "wiring up" outputs of mappings to the inputs of other mappings. Algebraic information flows along these "wires" in much the same way as along the wiring in a computer except that, in braided algebra, under-crossings and over-crossings represent non-trivial (and generally distinct) operations. This braided algebra is one of the deeper structures behind quantum groups and their associated brand of non-commutative geometry.

To make this precise, one adds to the notation for working in a braided category as follows. Recall that morphisms are generally represented by nodes on a string and understood flowing downwards. By definition, a braided algebra, or algebra in a braided category, means an object $B$ of the category, a product morphism $.: B \otimes B \rightarrow B$ and a unit morphism $\eta : \underline { 1 } \rightarrow B$, which is written as

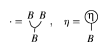
Figure: b120430a

by an extension of the notation. The associativity and unity axioms are then

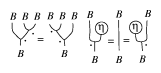
Figure: b120430b

In view of the associativity, one can also write multiple products as single nodes with multiple lines going in and one line coming out. Similarly, a braided co-algebra, or co-algebra in a braided category, is an object $B$ and morphisms $\Delta : B \rightarrow B \otimes B$ and $\varepsilon : B \rightarrow \underline{1}$, denoted by

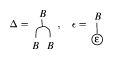
Figure: b120430c

and obeying co-associativity and co-unity axioms given by turning the above diagrams upside down.

Given two algebras $B$, $C$ in a braided category, one has a braided tensor product algebra $B \otimes \underline{ \ } C$ in the category. Its product is

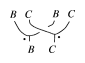
Figure: b120430d

In concrete cases, where $B$, $C$ are built on vector spaces, the product $B \otimes \underline{ \ } C$ is

\begin{equation*} ( a \bigotimes c ) ( b \bigotimes d ) = a \cdot \Psi _ { C , B } ( c \bigotimes b ) \cdot d \end{equation*}

for $a , b \in B$ and $c , d \in C$. This is a generalization of the supertensor product of two superalgebras.

It is now finally possible to define a braided group. This is $( B , \Delta , \varepsilon , S )$, where

a) $B$ is a unital algebra in a braided category;

b) $\Delta : B \rightarrow B \otimes B$ and $\varepsilon : B \rightarrow \underline{1}$ form a co-algebra in the braided category;

c) $\Delta$, $\varepsilon$ are algebra homomorphisms, where the braided tensor product algebra $B \otimes \underline{} B$ is used; here, $\Delta$, $\varepsilon$ respect the product in the sense

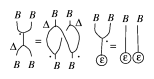
Figure: b120430e

d) $S : B \rightarrow B$ is a morphism obeying the diagram

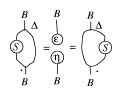
Figure: b120430f

It is a remarkable fact that most constructions in group theory go over to this "diagrammatic group theory" , i.e. work universally for all braided groups. For example, every braided group acts on itself by $\operatorname{Ad} : B \otimes B \rightarrow B$,

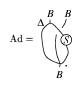
Figure: b120430g

The construction is modeled on the usual adjoint action of a group on itself, where

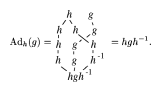
Figure: b120430h

Here, $\Delta$ models the diagonal mapping $h \rightarrow ( h , h )$ and $S$ models group inversion. There is an implicit transposition of $h$ past $g$ which becomes in the general case a non-trivial braiding $\Psi _ { B , B }$. Also in analogy with groups, one can show that the antipode is anti-multiplication preserving in the sense that

\begin{equation*} S\circ . = . \circ \Psi _ { B , B } \circ ( S \bigotimes S ) \end{equation*}

Examples.

Some basic examples of braided groups are the following. Let $k$ be a general field. Its invertible elements are denoted by $k ^ { * }$.

1) Fix $q \in k ^ { * }$. The braided line $\mathcal{A} _ { q }$ is $k [ x ]$ (polynomials in $x$) with the linear co-algebra and antipode

\begin{equation*} \Delta x = x \bigotimes 1 + 1 \bigotimes x, \end{equation*}

\begin{equation*} \varepsilon x = 0 , S x = - x \end{equation*}

and the braiding

\begin{equation*} \Psi ( x ^ { n } \bigotimes x ^ { m } ) = q ^ { n m } x ^ { m } \bigotimes x ^ { n } \end{equation*}

as an object in the braided category 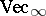of $\mathbf{Z}$-graded vector spaces. The braided group axioms above then determine that

\begin{equation*} \Delta x ^ { n } = \sum _ { m = 0 } ^ { n } \left[ \begin{array} { c } { n } \\ { m } \end{array} \right] _ { q } x ^ { n } \bigotimes x ^ { n - m } , S x ^ { n } = ( - 1 ) ^ { n } q ^ { n ( n - 1 ) / 2 } x ^ { n }, \end{equation*}

where

\begin{equation*} \left[\begin{array} { l } { n } \\ { m } \end{array} \right] _ { q } = \frac { [ n ] _{q} ! } { [ m ] _{q} ! [ n - m ] _{q} ! } ,\; [ m ]_{ q} = \frac { 1 - q ^ { m } } { 1 - q }, \end{equation*}

\begin{equation*} [ m ] _ { q } ! = [ m ] _ { q } [ m - 1 ] _ { q } \ldots [ 1 ] _ { q }. \end{equation*}

So, the $q$-integers $[ m ]_{ q}$ (which are ubiquitous throughout the theory of quantum groups) arise in the structure of the braided-line itself.

Similarly, when $q$ is an $n$th root of unity, one has an anyonic line $\mathcal{A} _ { n }$, defined in the same way but with the additional relation $x ^ { n } = 0$. It lives in the category $\operatorname{Vec}_n$ of $\mathbf{Z} / n \mathbf{Z}$-graded spaces as a generalization of Fermionic or Grassmann variables, where $n = 2$.

2) Fix $q \in k ^ { * }$. The quantum-braided plane $ \mathcal{A} _ { q } ^ { 2 }$ is $k \langle x , y \rangle$ (the free associative algebra generated by $x , y$) modulo the relations $y x = q x y$. The co-algebra and antipode are

\begin{equation*} \Delta x = x \bigotimes 1 + 1 \bigotimes x, \end{equation*}

\begin{equation*} \varepsilon x = 0 , S x = - x, \end{equation*}

\begin{equation*} \Delta y = y \bigotimes 1 + 1 \bigotimes y , \varepsilon y = 0, \end{equation*}

\begin{equation*} S _ { y } = - y, \end{equation*}

and the braiding is

\begin{equation*} \Psi ( x \bigotimes x ) = q ^ { 2 } x \bigotimes x, \end{equation*}

\begin{equation*} \Psi ( y \bigotimes y ) = q ^ { 2 } y \otimes y \Psi ( x \otimes y ) = q y \otimes x \end{equation*}

\begin{equation*} \Psi ( y \bigotimes x ) = q x \bigotimes y + ( q ^ { 2 } - 1 ) y \bigotimes x. \end{equation*}

The braiding here is the same one which gives rise to the Jones knot invariant; the braided group lives in the category of $U _ { q } (\operatorname{ gl} _ { 2 } )$-modules or $\operatorname {GL} _ { q } ( 2 )$-co-modules (see Quasi-triangular Hopf algebra).

Similarly, there are quantum-braided planes covariantly associated to other quantum groups, or, more generally, braided co-vectors $V ^ { * } ( R ^ { \prime } , R )$ associated to any invertible matrix $R$ of the Yang–Baxter equation and a suitable matrix $R ^ { \prime }$. They have the general form $k \langle x _ { i } \rangle$ with relations and braiding

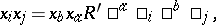\begin{equation*} \Psi ( x _ { i } \bigotimes x _ { j } ) = x _ { b } \bigotimes x _ { a } R ^ { a } \square _ { i } \square ^ { b } \square_{j} \end{equation*}

(summations in repeated indices). A common misconception is that associativity requires $R ^ { \prime }$ to obey the Yang–Baxter equations. In fact, it is $R$ in the braiding which requires this.

3) For $q \in k ^ { * }$, there is a braided group $U _ { q } ( n _ { + } )$ associated to any symmetrizable Cartan matrix. For example, $U _ { q } ( n _ { + } )$ for $\mathbf{sl} _ { 3 }$ is $k \langle E _ { 1 } , E _ { 2 } \rangle$ modulo the $q$-Serre relations

\begin{equation*} E _ { 1 } ^ { 2 } E _ { 2 } + E _ { 2 } E _ { 1 } ^ { 2 } - ( q + q ^ { - 1 } ) E _ { 1 } E _ { 2 } E _ { 1 } = 0, \end{equation*}

\begin{equation*} E _ { 2 } ^ { 2 } E _ { 1 } + E _ { 1 } E _ { 2 } ^ { 2 } - ( q + q ^ { - 1 } ) E _ { 2 } E _ { 1 } E _ { 2 } = 0. \end{equation*}

The co-algebra and antipode on the generators have the same linear form as above but the braiding is

\begin{equation*} \Psi ( E _ { i } \bigotimes E _ { j } ) = q ^ { a _ { i j} } E _ { j } \bigotimes E _ { i }, \end{equation*}

where $a _ { i j}$ is the standard Cartan matrix of $\mathbf{sl} _ { 3 }$. Similar results hold when $n _ { + }$ is the nil radical of the Borel subalgebra of a complex semi-simple or Kac–Moody Lie algebra $\frak g$. These $U _ { q } ( n _ { + } )$ have a natural Kashiwara–Lusztig canonical basis.

4) There are braided group enveloping algebras $B U _ { q } ( \mathfrak{g} )$ deforming the universal enveloping algebras (cf. also Universal enveloping algebra) of all complex semi-simple Lie algebras $\frak g$. They live in the category of $U _ { q } ( \mathfrak { g } )$-modules under the adjoint action. In fact, they have the same algebra as the quantum group enveloping algebra $U _ { q } ( \mathfrak { g } )$ (see Quasi-triangular Hopf algebra) but a different co-product.

In a general algebraic formulation, every quasi-triangular Hopf algebra $( H , \mathcal{R} )$ has a braided version $B ( H )$ living in the category of $H$-modules by the adjoint action. This is called the transmutation of $H$ to a braided group $B ( H )$.

5) There are braided group coordinate rings $BG_{q}$ which are braided versions of the usual quantum group coordinate rings $G_q$. They are built on the same co-algebra with a modified product and live in the category of $G_q$-co-modules by the adjoint action.

For example, for $q \in k ^ { * }$, the braided group $B \operatorname {SL} _ { q } ( 2 )$ is $k \langle \alpha , \beta , \gamma , \delta \rangle$ modulo the relations

\begin{equation*} \beta \alpha = q ^ { 2 } \alpha \beta, \end{equation*}

\begin{equation*} \gamma \alpha = q ^ { - 2 } \alpha \gamma , \delta \alpha = \alpha \delta, \end{equation*}

\begin{equation*} \beta \gamma = \gamma \beta + ( 1 - q ^ { - 2 } ) \alpha ( \delta - \alpha ) , \delta \beta = \beta \delta + ( 1 - q ^ { - 2 } ) \alpha \beta, \end{equation*}

\begin{equation*} \gamma \delta = \delta \gamma + ( 1 - q ^ { - 2 } ) \gamma \alpha , \end{equation*}

and the "braided q-determinant" relation

\begin{equation*} \alpha \delta - q ^ { 2 } \gamma \beta = 1. \end{equation*}

The co-algebra is

\begin{equation*} \Delta \left( \begin{array} { c c } { \alpha } & { \beta } \\ { \gamma } & { \delta } \end{array} \right) = \left( \begin{array} { c c } { \alpha } & { \beta } \\ { \gamma } & { \delta } \end{array} \right) \bigotimes \left( \begin{array} { c c } { \alpha } & { \beta } \\ { \gamma } & { \delta } \end{array} \right), \end{equation*}

\begin{equation*} \varepsilon \left( \begin{array} { l l } { \alpha } & { \beta } \\ { \gamma } & { \delta } \end{array} \right) = \left( \begin{array} { l l } { 1 } & { 0 } \\ { 0 } & { 1 } \end{array} \right) \end{equation*}

(matrix multiplication understood) and the antipode is

\begin{equation*} S \left( \begin{array} { c c } { \alpha } & { \beta } \\ { \gamma } & { \delta } \end{array} \right) = \left( \begin{array} { c c } { q ^ { 2 } \delta + ( 1 - q ^ { 2 } ) \alpha } & { - q ^ { 2 } \beta } \\ { - q ^ { 2 } \gamma } & { \alpha } \end{array} \right). \end{equation*}

The braiding is

\begin{equation*} \Psi ( \alpha \bigotimes \alpha ) = \alpha \bigotimes \alpha + ( 1 - q ^ { 2 } ) \beta \bigotimes \gamma, \end{equation*}

\begin{equation*} \Psi ( \alpha \bigotimes \beta ) = q \beta \bigotimes \alpha, \end{equation*}

etc. ($16$ relations).

In a general algebraic formulation, every dual quasi-triangular Hopf algebra has a braided version with the same co-algebra and a modified product, called its transmutation. It lives in the braided category of co-modules of the Hopf algebra by the adjoint co-action.

6) In an $R$-matrix formulation, there is a braided bi-algebra of braided matrices $B ( R )$ associated to every bi-invertible solution $R$ of the Yang–Baxter equations. This is $k \langle u ^ { i } \square_{ j} \rangle$ (a matrix of generators) modulo relations

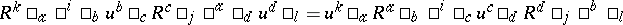(summation of repeated indices). The co-algebra has the matrix form

\begin{equation*} \Delta u ^ { i } \square_j = u ^ { i } \square _ { a } \bigotimes u ^ { a } \square_j , \varepsilon u ^ { i } \square_j = \delta ^ { i } \square_j \end{equation*}

(summation over $a$) and the braiding is defined by

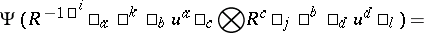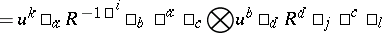(summation over repeated indices). A spectral parameter version of the algebra here occurs in the theory of integrable systems as Cherednik's reflection equations. The quadratic algebras $B ( R )$ themselves arose in the theory of braided groups by transmutation from the quantum matrices $A ( R )$ (see Quasi-triangular Hopf algebra). It is for this reason that they have many similar properties to the latter.

7) Given a braided group $B$ in the category of (co-)modules of a ({co-})quasi-triangular Hopf algebra $H$, one has an ordinary Hopf algebra $B \rtimes H$, called its bosonization. It is such that the (co-)modules of $B$ in the braided category are in one-to-one correspondence with the (co-)modules of $B \rtimes H$.

More generally, given a braided group $B \in \square _ { H } ^ { H } \mathcal{M}$, the category of crossed modules under $H$ (with invertible antipode), one has an ordinary Hopf algebra $B \rtimes H$ (an algebra cross product by the action of $H$ and a co-algebra cross product by the co-action of $H$). Conversely, let $H _ { 1 } \rightarrow H$ be a surjection between Hopf algebras split by a Hopf algebra inclusion $H \rightarrow H _ { 1 }$, and assume that $H$ has an invertible antipode. Then it can be shown that $H _ { 1 } = B \rtimes H$ for some braided group $B \in \square _ { H } ^ { H } \mathcal{M}$.

For example, the bosonization of the quantum-braided plane is the Hopf algebra $\mathcal{A} _ { q } ^ { 2 } \rtimes \operatorname { GL} _ { q } ( 2 )$. One similarly constructs Poincaré and other inhomogeneous quantum groups by bosonization of braided groups.

There is also a "double bosonization" construction $B \rtimes H \ltimes B ^ { * }$ when a braided group $B$ is equipped with a suitable dual $B ^ { * }$. In particular, this allows the inductive construction of all quantum groups $U _ { q } ( \mathfrak { g } )$ by repeatedly adjoining braided planes of additional roots and their duals. It also allows one to construct $U _ { q } ( {\frak g} ) = U _ { q } ( n _ { - } ) {\color{blue} \rtimes} H {\color{blue} \ltimes } U _ { q } ( n _ { + } )$, a version of $U _ { q } ( \mathfrak { g } )$ due to G. Lusztig. Here, $H$ is the Cartan or torus part viewed as a commutative dual quasi-triangular Hopf algebra.

Transmutation, bosonization and double bosonization provide a close relationship between quantum groups and braided groups, allowing the diagrammatic methods to be applied to the latter (rather than inserting $q$ randomly here and there). As well as providing a systematic approach, there is a theory of braided-Lie algebras which provides a finite-dimensional object generating $B U _ { q } ( \mathfrak{g} )$ (and hence $U _ { q } ( \mathfrak { g } )$) as some kind of enveloping algebra.

There are some remarkable and unexpected consequences as well, with no $q = 1$ analogue. One of them is that $B U _ { q } ( \mathfrak{g} )$ and $BG_{q}$ are essentially isomorphic as braided groups. They are also dual to each other, i.e. the braided versions are essentially self-dual. This self-duality isomorphism is singular when $q \rightarrow 1$. Consequently, $B U _ { q } ( \mathfrak{g} )$ and hence $U _ { q } ( \mathfrak { g } )$, although an analogue of an enveloping algebra, can be described when $q \neq 1$ as an analogue of an algebraic-group coordinate algebra by a matrix of generators and relations. One has to take certain versions of these algebras for a precise isomorphism here.

As well applications to quantum groups, braided groups have their own intrinsic braided geometry. For example, in the braided line one can define braided differentiation $\partial _ { q }$ as an infinitesimal translation via the braided co-product. Thus,

\begin{equation*} \Delta f = 1 \bigotimes f + x \bigotimes \partial _ { q } f +\dots \end{equation*}

for any polynomial $f ( x )$ in the braided line. This works out as

\begin{equation*} \partial _ { q } f ( x ) = \frac { f ( x ) - f ( q x ) } { x ( 1 - q ) } , \quad \partial _ { q } x ^ { n } = [ n ] _ { q } x ^ { n - 1 }, \end{equation*}

which occurs in the theory of $q$-special functions. Similarly, one can define the partial braided derivatives 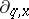and $\partial _ { q , y}$ on the quantum braided plane by

\begin{equation*} \Delta f = 1 \bigotimes f + x \bigotimes \partial _ { q , x } \,f + y \bigotimes \partial _ { q , y } \,f +\dots , \end{equation*}

which comes out as

\begin{equation*} \partial _ { q , x } ( x ^ { n } y ^ { m } ) = [ n ] _ { q ^ { 2 } } x ^ { n - 1 } y ^ { m }, \end{equation*}

\begin{equation*} \partial _ { q , y } ( x ^ { n } y ^ { m } ) = q ^ { n } [ m ] _ { q ^ { 2 } } x ^ { n } y ^ { m - 1 }. \end{equation*}

One also has a braided Taylor theorem, braided exponentials, etc. This naturally extends the theory of $q$-special functions to higher dimensions as the braided geometry of quantum-braided planes. Note that non-trivial co-products of the above linear form on the generators are not possible in the context of ordinary Hopf algebras.

References

[a1]	S. Majid, "Examples of braided groups and braided matrices" J. Math. Phys. , 32 (1991) pp. 3246–3253
[a2]	S. Majid, "Algebras and Hopf algebras in braided categories" , Lecture Notes Pure Appl. Math. , 158 , M. Dekker (1994) pp. 55–105
[a3]	S. Majid, "Foundations of quantum group theory" , Cambridge Univ. Press (1995)
[a4]	S. Majid, "Double bosonisation and the construction of $U _ { q } ( \mathfrak { g } )$" Math. Proc. Cambridge Philos. Soc. , 125 (1999) pp. 151–192