Belousov-Zhabotinskii reaction

symbolic dynamics in the

The Belousov–Zhabotinskii reaction has revealed most of the well-known routes to chaos, including period-doubling, intermittency, quasi-periodicity, frequency locking, and fractal torus [a1], [a2], [a3], [a4], [a5]. However, although the data have been shown to display unambiguous features of deterministic chaos, the understanding of the nature and the origin of the observed behaviour has been incomplete. In 1976, O.E. Rössler suggested an intuitive interpretation to explain chemical chaos. His feeling was that non-periodic wandering trajectories might arise in chemical systems from a pleated slow manifold (Fig.a1a), if the flow on the lower surface of the pleat had the property of returning trajectories to a small neighbourhood of an unstable focus lying on the upper surface. More recently, Rössler's terminology of spiral-type, screw-type and funnel-type strange attractors has been revisited in terms of chaotic orbits that occur in nearly homoclinic conditions [a6]. By Shil'nikov's theorem, there exist uncountably many non-periodic trajectories in systems that display a homoclinic orbit bi-asymptotic to a saddle-focus at $ O $, provided that $ {\rho / \lambda } <1 $, where the eigenvalues of $ O $ are $ ( - \lambda, \rho \pm i \omega ) $. This subset of chaotic trajectories is actually in one-to-one correspondence with a shift automorphism with an infinite number of symbols. Since homoclinic orbits are structurally unstable objects lying on codimension-one hypersurfaces in the constraint space, one can reasonably hope to cross these hypersurfaces when following a one-parameter path. The bifurcation structure encountered near homoclinic orbits involves infinite sequences of saddle-node and period-doubling bifurcations.

Some numerical and experimental evidences for Shil'nikov homoclinic chaos in non-equilibrium chemical systems are obtained in [a7], [a8].

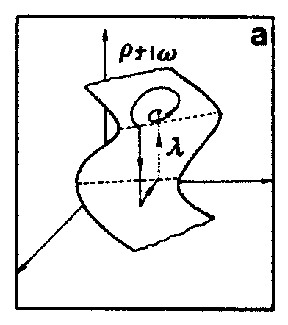
Figure: b110260a

A homoclinic re-injection process resulting from a slow manifold effect

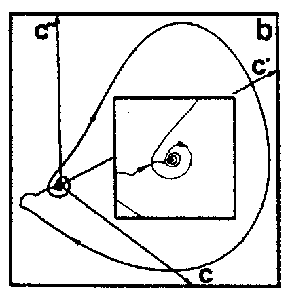
Figure: b110260b

The homoclinic re-injection process observed in a Belousov–Zhabotinskii experiment; only a part of the time series is shown

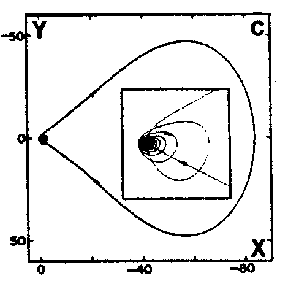
Figure: b110260c

Homoclinic orbit computed in a $ 3 $- dimensional Rössler-like model

Poincaré map model for homoclinic chaos.

To connect Rössler's intuition to Shil'nikov's mathematical results, one can use a geometrical approach to construct a Poincaré return map model for homoclinic chaos [a7], [a8]. This approach consists in constructing a simple model of the flow that retains the two essential features of the flow near homoclinicity: i) an orbit close to a homoclinic orbit spends most of its time near the saddle-focus $ O $ where the dynamics is approximately linear; and ii) the non-linear properties of the flow are such that the trajectories return to a small neighbourhood of $ O $. Assuming the re-injection process to be a rigid motion, one obtains a $ 2 $- dimensional Poincaré map model, which reduces to the following $ 1 $- dimensional mapping in the infinite area contraction limit:

$$ X ^ \prime = \sqrt {X ^ {2} + {\widetilde{y} } ^ {2} } e ^ { {{( { {{ \mathop{\rm arctan} } {\widetilde{y} } } / X } + k \pi ) \rho } / \omega } } - X _ {H} + {\widetilde{x} } , $$

where the parameters $ \lambda $, $ \rho $, $ \omega $ characterize the dynamics near the saddle focus while $ X _ {H} , {\widetilde{x} } $ and $ {\widetilde{y} } $ parametrize the non-linear re-injection process. $ {\widetilde{x} } $ and $ {\widetilde{y} } $ measure the deviation from homoclinicity ( $ {\widetilde{x} } = {\widetilde{y} } = 0 $). $ k $ is an integer, corresponding to the number of half-turns the trajectory completes around the saddle-focus in between two successive crossings of the Poincaré plane that must be chosen transverse to the re-injection process. Fig.a2a illustrates the $ 1 $- dimensional mapping of a "spiral-type" strange attractor at homoclinicity. This piecewise-linear mapping contains an infinite number of increasing branches, which converge geometrically to $ X =0 $ with ratio $ \delta = { \mathop{\rm exp} } ( { {- 2 \pi \rho } / \omega } ) $. A symbol $ k = 2m $( even) is assigned to each of these branches. "Spiral-type" strange attractors are such that the re-injection process returns the trajectories on one side of the saddle-focus only. Therefore, the number of half-turns of the trajectories around it is either even, $ k = 2m $( increasing branches), or odd, $ k = 2m + 1 $( decreasing branches). Since for "screw-type" strange attractors the re-injection process returns the trajectories on both sides of $ O $, the corresponding $ 1 $- dimensional mapping exhibits infinite sequences of increasing ( $ k = 2m $) and decreasing ( $ k = 2m + 1 $) branches, which both converge geometrically to $ X = 0 $, as shown in Fig.a2b. At finite distance from homoclinicity, the $ 1 $- dimensional mapping of "screw-type" strange attractors contains only a finite number of increasing and decreasing branches, separated by a quadratic well (Fig.a2c). When approaching homoclinicity, the successive disappearances (at the bottom) and re-appearances (at the top) of the well in the invariant square governs the creation of new branches via a cascade of saddle-node bifurcations [a6].

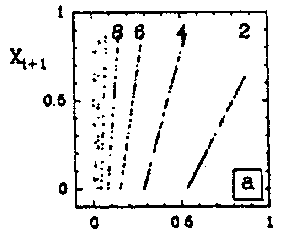
Figure: b110260d

"Spiral-type" strange attractor at homoclinicity

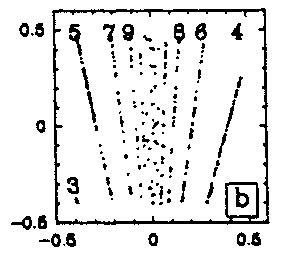
Figure: b110260e

"Screw-type" strange attractor at homoclinicity

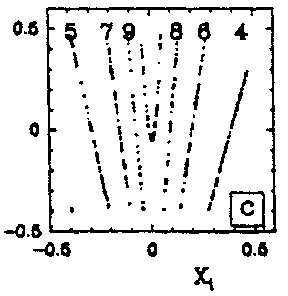
Figure: b110260f

"Screw-type" strange attractor at finite distance from homoclinicity

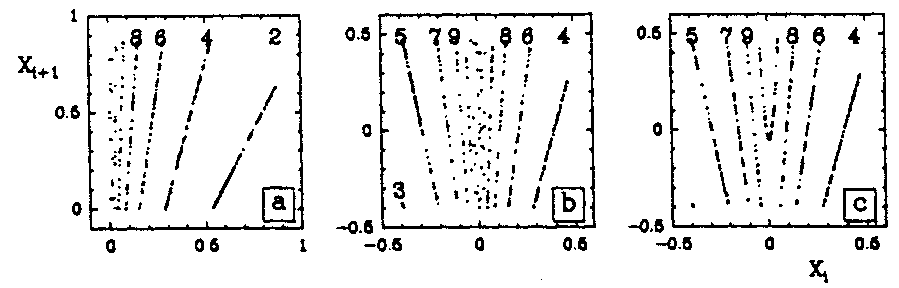
Figure: b110260g

Sets of iterates of the $ 1 $- dimensional mapping model

Homoclinic chaos in a seven-variable Oregonator model.

The controversy about the deterministic or stochastic character of chemical chaos has been essentially perpetuated by numerical simulations [a1], [a2], [a3], [a4], [a5]. In fact, none among all the chemical models proposed has been able to reproduce the scenarios to chaos observed in bench experiments. Recently, some success has been recorded in reproducing most of the alternating periodic-chaotic sequences detected in experiments with a seven-variable Oregonator model which retains the main steps of the F.K.N. model of the Belousov–Zhabotinskii reaction [a4], [a5]. While these simulations of experimental sequences have dispelled all doubts about the deterministic nature of chemical chaos, the striking resemblance of some $ 1 $- dimensional mappings obtained with this Oregonator model (Fig.a3), with the multi-branched $ 1 $- dimensional mapping model (Fig.a2) strongly indicates that the "screw-type" strange attractors observed along these sequences are the precursors to Shil'nikov's homoclinic chaos [a7], [a8], [a6].

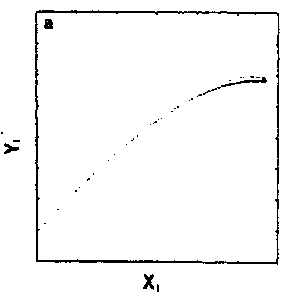
Figure: b110260h

Poincaré map

Figure: b110260i

The corresponding $ 1 $- dimensional mapping

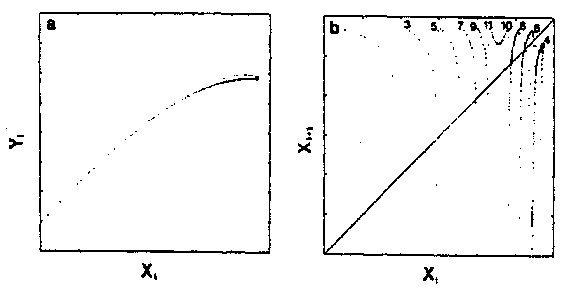
Figure: b110260j

Simulation of a "screw-type" strange attractor with a seven-variable Oregonator model

Experimental evidence for homoclinic chaos.

To conclude definitely the homoclinic nature of chemical chaos, some convincing experimental results have been obtained with the Belousov–Zhabotinskii reaction [a7], [a8]. On increasing the flow rate from low values, the thermodynamic branch has been traced up to a critical value (subcritical Hopf bifurcation), where a discontinuous transition leads to non-periodic oscillations (Fig.a4a). Apparently, at random a large amplitude oscillation occurs and is followed by an episode of small amplitude oscillations, the envelop of which increases nearly exponentially. The trajectory returns once in a while to the vicinity of a saddle-focus and close enough (Fig.a1b) so that the phase portrait looks like a "spiral-type" strange attractor (Fig.a4b). This observation is confirmed when reconstructing a $ 2 $- dimensional Poincaré map (Fig.a4c): the whole set of experimental points is, to a good approximation, located along a smooth curve. This attests that the dynamics is attracted to a nearly $ 2 $- dimensional fractal surface with a strong transverse packing of the sheets of the attractor. The corresponding $ 1 $- dimensional mapping is shown in Fig.a4d; a symbol $ m $( $ k = 2m + 1 $) has been assigned to each point of this $ 1 $- dimensional mapping according to the number $ m $ of small amplitude oscillations which immediately follow the homoclinic re-injection. Thus, $ m $ is the number of small amplitude oscillations in a basic pattern in the time series (Fig.a4a). The distribution of the symbols in Fig.a4d displays some ordering which appears to be consistent with the theoretical ordering for "spiral-type" strange attractor in nearly homoclinic condition. Regarding the experimental uncertainty, the points associated with the same symbol fall roughly in vertical strips; moreover $ m $ increases (from $ 0 $ to $ 8 $) from the left to the right of the figure, which is the clue that the chronology of patterns in the time-series in Fig.a4a conforms to the symbolic dynamics predicted by Shil'nikov's theory of homoclinic chaos. The reproduction in Fig.a5 of the experimental situation in a low-dimensional differential system of Rössler type consolidates the homoclinic appellation for the data shown in Fig.a4. This is the first experimental proof of the homoclinic nature of the chemical chaos occurring in the Belousov–Zhabotinskii experiment [a7], [a8], [a6].

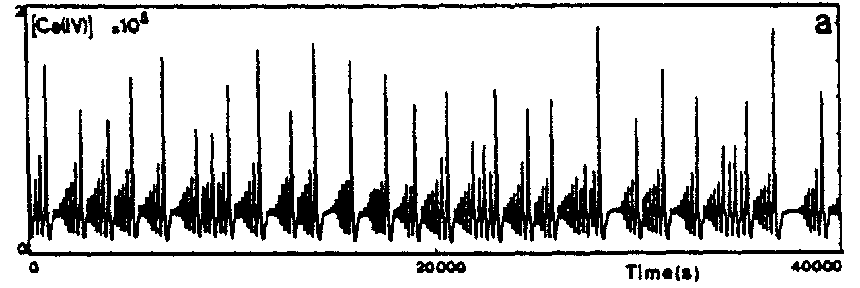
Figure: b110260k

Time series

Figure: b110260l

Phase portrait

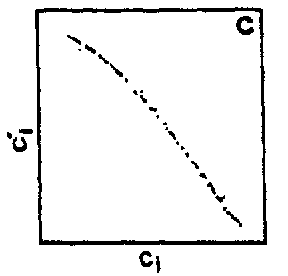
Figure: b110260m

Poincaré map

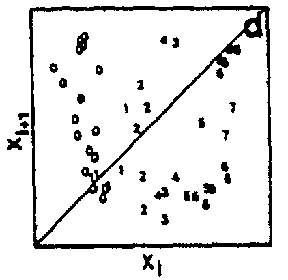
Figure: b110260n

$ 1 $- dimensional mapping

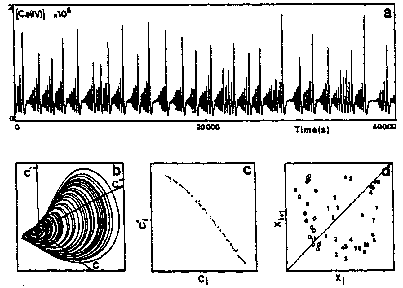
Figure: b110260o

Experimental homoclinic chaos observed in the Belousov–Zhabotinskii reaction

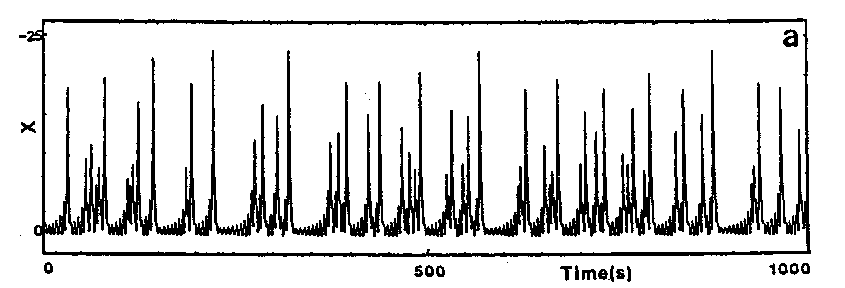
Figure: b110260p

Time series

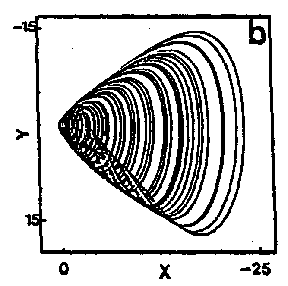
Figure: b110260q

Phase portrait

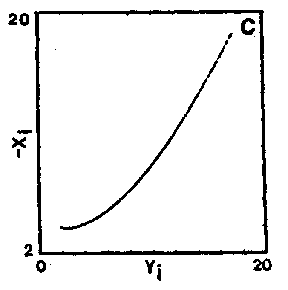
Figure: b110260r

Poincaré map

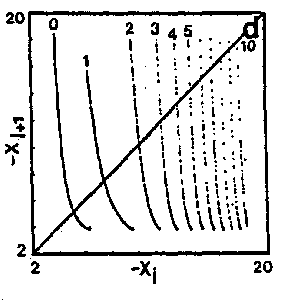
Figure: b110260s

$ 1 $- dimensional mapping

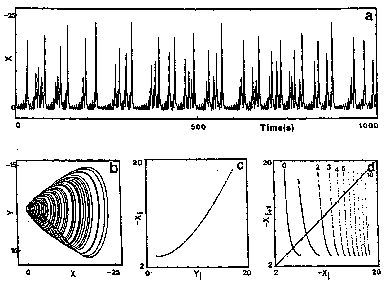
Figure: b110260t

Homoclinic chaos computed with a $ 3 $- dimensional ordinary differential system in conditions close to the subcritical Hopf bifurcation of the origin $ O $( in order to mimic the experimental situation in Fig.a4)

References

[a1]	"Nonlinear phenomena in chemical dynamics" C. Vidal (ed.) A. Pacault (ed.) , Springer (1981)
[a2]	C. Vidal, A. Pacault, "Nonequilibrium dynamics in chemical systems" , Springer (1984)
[a3]	"Spatial inhomogeneities and transient behaviour in chemical kinetics" P. Gray (ed.) G. Nicolis (ed.) F. Baras (ed.) P. Borckmans (ed.) S.K. Scott (ed.) , Manchester Univ. Press (1990)
[a4]	A. Arneodo, F. Argoul, P. Richetti, J.C. Roux, "The Belousov–Zhabotinskii reaction: a paradigm for theoretical studies of dynamical systems" H.G. Bothe (ed.) W. Ebeling (ed.) A.M. Zurzhanski (ed.) M. Peschel (ed.) , Dynamical Systems and Environmental Models , Akademie Verlag (1987) pp. 122
[a5]	F. Argoul, A. Arneodo, P. Richetti, J.C. Roux, H.L. Swinney, "Chaos in chemical systems: from hints to confirmation" Acc. Chem. Res. , 20 (1987) pp. 436
[a6]	P. Gaspard, A. Arneodo, R. Kapral, C. Sparrow, "Homoclinic chaos" Physica D , 62 (1993) pp. 1–372
[a7]	F. Argoul, A. Arneodo, P. Richetti, "Symbolic dynamics in the Belousov–Zhabotinskii reaction: from Rössler's intuiton to experimental evidence for Shil'nikov's homoclinic chaos" G. Baier (ed.) M. Klein (ed.) , A Chaotic Hierarchy , World Sci. (1991) pp. 79 (Phys. Lett. 120A (1987), 269)
[a8]	A. Arneodo, F. Argoul, J. Elezgaray, P. Richetti, "Homoclinic chaos in chemical systems" Physica D , 62 (1993) pp. 134

🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️