ANOVA

analysis of variance

Here, ANOVA will be understood in the wide sense, i.e., equated to the univariate linear model whose model equation is

\begin{equation} \tag{a1} \bf y = X \beta + e, \end{equation}

in which $\mathbf{y}$ is an $n \times 1$ observable random vector, $\mathbf{X}$ is a known $( n \times m )$-matrix (the "design matrix" ), $\beta$ is an $( m \times 1 )$-vector of unknown parameters, and is an $( n \times 1 )$-vector of unobservable random variables $e _ { i }$ (the "errors" ) that are assumed to be independent and to have a normal distribution with mean $0$ and unknown variance $\sigma ^ { 2 }$ (i.e., the $e _ { i }$ are independent identically distributed $N ( 0 , \sigma ^ { 2 } )$). It is assumed throughout that $n > m$. Inference is desired on $\beta$ and $\sigma ^ { 2 }$. The $e _ { i }$ may represent measurement error and/or inherent variability in the experiment. The model equation (a1) can also be expressed in words by: $\mathbf{y}$ has independent normal elements $y _ { i }$ with common, unknown variance and expectation $\mathsf E ( \mathbf y ) = \mathbf X \beta$, in which $\mathbf{X}$ is known and $\beta$ is unknown. In most experimental situations the assumptions made on should be regarded as an approximation, though often a good one. Studies on some of the effects of deviations from these assumptions can be found in [a48], Chap. 10, and [a51] discusses diagnostics and remedies for lack of fit in linear regression models. To a certain extent the ANOVA ideas have been carried over to discrete data, then called the log-linear model; see [a6], and [a10].

MANOVA (multivariate analysis of variance) is the multivariate generalization of ANOVA. Its model equation is obtained from (a1) by replacing the column vectors $\mathbf{y} , \beta , \mathbf{e}$ by matrices $\mathbf{Y} , \mathbf{B} , \mathbf{E}$ to obtain

\begin{equation} \tag{a2} \bf Y = X B + E, \end{equation}

where $\mathbf{Y}$ and $\mathbf{E}$ are $n \times p$, $\mathbf{B}$ is $m \times p$, and $\mathbf{X}$ is as in (a1). The assumption on $\mathbf{E}$ is that its $n$ rows are independent identically distributed $N ( 0 , \Sigma )$, i.e., the common distribution of the independent rows is $p$-variate normal with $0$ mean and $p \times p$ non-singular covariance matrix $\Sigma$.

GMANOVA (generalized multivariate analysis of variance) generalizes the model equation (a2) of MANOVA to

\begin{equation} \tag{a3} \mathbf{Y} = \mathbf{X} _ { 1 } \mathbf{BX} _ { 2 } + \mathbf{E}, \end{equation}

in which $\mathbf{E}$ is as in (a2), $\mathbf{X} _ { 1 }$ is as $\mathbf{X}$ in (a2), $\mathbf{B}$ is $m \times s$, and $\mathbf{X} _ { 2 }$ is an $s \times p$ second design matrix.

Logically, it would seem that it suffices to deal only with (a3), since (a2) is a special case of (a3), and (a1) of (a2). This turns out to be impossible and it is necessary to treat the three topics in their own right. This will be done, below. For unexplained terms in the fields of estimation and testing hypotheses, see [a30], [a31] (and also Statistical hypotheses, verification of; Statistical estimation).

ANOVA.

This field is very large, well-developed, and well-documented. Only a brief outline is given here; see the references for more detail. An excellent introduction to the essential elements of the field is [a48] and a short history is given in [a47], Sect. 2. Brief descriptions are also given in [a56], headings Anova; General Linear Model. Other references are [a49] [a50], [a43], [a26], and [a15]. A collection of survey articles on many aspects of ANOVA (and of MANOVA and GMANOVA) can be found in [a14].

In (a1) it is assumed that the parameter vector $\beta$ is fixed (even though unknown). This is called a fixed effects model, or Model I. In some experimental situations it is more appropriate to consider $\beta$ random and inference is then about parameters in the distribution of $\beta$. This is called a random effects model, or Model II. It is called a mixed model if some elements of $\beta$ are fixed, others random. There are also various randomization models that are not described by (a1). For reasons of space limitation, only the fixed effects model will be treated here. For the other models see [a48], Chaps. 7, 8, 9.

The name "analysis of variance" was coined by R.A. Fisher, who developed statistical techniques for dealing with agricultural experiments; see [a48], Sect. 1.1: references to Fisher. As a typical example, consider the two-way layout for the simultaneous study of two different factors, for convenience denoted by $\mathbf{A}$ and $\operatorname{B}$, on the measurement of a certain quantity. Let $\mathbf{A}$ have levels $i = 1 , \ldots , I$, and let $\operatorname{B}$ have levels $j = 1 , \ldots , J$. For each $( i , j )$ combination, measurements $y _ { i j k }$, $k = 1 , \ldots , K$, are made. For instance, in a study of the effects of different varieties and different fertilizers on the yield of tomatoes, let $y _ { i j k }$ be the weight of ripe tomatoes from plant $k$ of variety $i$ using fertilizer $j$. The model equation is

\begin{equation} \tag{a4} y _ { i j k } = \mu + \alpha _ { i } + \beta _ { j } + \gamma _ { i j } + e _ { i j k }, \end{equation}

and it is assumed that the $e _ {i j k }$ are independent identically distributed $N ( 0 , \sigma ^ { 2 } )$. This is of the form (a1) after the $y _ { i j k }$ and $e _ {i j k }$ are strung out to form the column vectors $\mathbf{y}$ and of (a1) with $n = I J K$; similarly, the parameters on the right-hand side of (a4) form an $( m \times 1 )$-vector $\beta$, with $m = 1 + I + J + I J$; finally, $\mathbf{X}$ in (a1) has one column for each of the $m$ parameters, and in row $( i , j , k )$ of $\mathbf{X}$ there is a $1$ in the columns for $\mu$, $\alpha_i$, $\beta_j$, and $\gamma _ { i j }$, and $0$s elsewhere. Some of the customary terminology is as follows. Each $( i , j )$ combination is a cell. In the example (a4), each cell has the same number $K$ of observations (balanced design); in general, the cell numbers need not be equal. The parameters on the right-hand side of (a4) are called the effects: $\mu$ is the general mean, the $\alpha$s are the main effects for factor $\mathbf{A}$, the $\beta$s for $\operatorname{B}$, and the $\gamma$s are the interactions.

The extension to more than two factors is immediate. There are then potentially more types of interactions; e.g., in a three-way layout there are three types of two-factor interactions and one type of three-factor interactions. Layouts of this type are called factorial, and completely crossed if there is at least one observation in each cell. The latter may not always be feasible for practical reasons if the number of cells is large. In that case it may be necessary to restrict observations to only a fraction of the cells and assume certain interactions to be $0$. The judicious choice of this is the subject of design of experiments; see [a26], [a15].

A different type of experiment involves regression. In the simplest case the measurement $y$ of a certain quantity may be modelled as $y = \alpha + \beta t +\text{error}$, where $\alpha$ and $\beta$ are unknown real-valued parameters and $t$ is the value of some continuously measurable quantity such as time, temperature, distance, etc.. This is called linear regression (i.e., linear in $t$). More generally, there could be an arbitrary polynomial in $t$ on the right-hand side. As an example, assume quadratic regression and suppose $t$ denotes time. Let $y _ { i }$ be the measurement on $y$ at time $t_i$, $i = 1 , \dots , n$. The model equation is $y _ { i } = \alpha + \beta t _ { i } + \gamma t_{i} ^ { 2 } + e _ { i }$, which is of the form (a1) with $( \alpha , \beta , \gamma ) ^ { \prime } = \beta$ of (a1). The matrix $\mathbf{X}$ of (a1) has three columns corresponding to $\alpha$, $\beta$, and $\gamma$; the $i$th row of $\mathbf{X}$ is $( 1 , t _ { i } , t _ { i } ^ { 2 } )$. Functions of $t$ other than polynomials are sometimes appropriate. Frequently, $t$ is referred to as a regressor variable or independent variable, and $y$ the dependent variable. Instead of one regressor variable there may be several (multiple regression).

Factors such as $t$ above whose values can be measured on a continuous scale are called quantitative. In contrast, categorical variables (e.g., variety of tomato) are called qualitative. A quantitative factor $t$ may be treated qualitatively if the experiment is conducted at several values, say $t _ { 1 } , t _ { 2 } , \ldots$, but these are only regarded as levels $i = 1,2 , \dots$ of the factor whereas the actual values $t _ { 1 } , t _ { 2 } , \ldots$ are ignored. The name analysis of variance is often reserved for models that have only factors that are qualitative or treated qualitatively. In contrast, regression analysis has only quantitative factors. Analysis of covariance covers models that have both kinds of factors. See [a48], Chap. 6, for more detail.

Another important distinction involving factors is between the notions of crossing and nesting. Two factors $\mathbf{A}$ and $\operatorname{B}$ are crossed if each level of $\mathbf{A}$ can occur with each level of $\operatorname{B}$ (completely crossed if there is at least one observation for each combination of levels, otherwise incompletely or partly crossed). For instance, in the tomato example of the two-way layout (a4), the two factors are crossed since each variety $i$ can be grown with any fertilizer $j$. In contrast, factor $\operatorname{B}$ is said to be nested within factor $\mathbf{A}$ if every level of $\operatorname{B}$ can only occur with one level of $\mathbf{A}$. For instance, suppose two different manufacturing processes (factor $\mathbf{A}$) for the production of cords have to be compared. From each of the two processes several cords are chosen (factor $\operatorname{B}$), each cord cut into several pieces and the breaking strength of each piece measured. Here each cord goes only with one of the processes so that $\operatorname{B}$ is nested within $\mathbf{A}$. Nested factors should be treated more realistically as random. However, for the analysis it is necessary to analyze the corresponding fixed effects model first. See [a48], Sect. 5.3, for more examples and detail.

Estimation and testing hypotheses.

The main interest is in inference on linear functions of the parameter vector $\beta$ of (a1), called parametric functions, i.e., functions of the form $\psi = \mathbf{c} ^ { \prime } \beta$, with $\mathbf{c}$ of order $m \times 1$. Usually one requires point estimators (cf. also Point estimator) of such $\psi$s to be unbiased (cf. also Unbiased estimator). Of particular interest are the elements of the vector $\beta$. However, there is a complication arising from the fact that the design matrix $\mathbf{X}$ in (a1) may be of less than maximal rank (the columns can be linearly dependent). This happens typically in analysis of variance models (but not usually in regression models). For instance, in the two-way layout (a4) the sum of the columns for the $\alpha_i$ equals the column for $\mu$. If $\mathbf{X}$ is of less than full rank, then the elements of $\beta$ are not identifiable in the sense that even if the error vector in (a1) were $0$, so that $\mathbf{X} \beta$ is known, there is no unique solution for $\beta$. A fortiori the elements of $\beta$ do not possess unbiased estimators. Yet, there are parametric functions that do have an unbiased estimator; they are called estimable. It is easily shown that $\mathbf{c} ^ { \prime } \beta$ is estimable if and only if $\mathbf{c} ^ { \prime }$ is in the row space of $\mathbf{X}$ (see [a48], Sect. 1.4). In particular, if one sets $\mathsf E ( y _ { i } ) = \eta _ { i }$ and takes $\mathbf{c} ^ { \prime }$ to be the $i$th row of $\mathbf{X}$, then $\mathbf{c} ^ { \prime } \beta = \eta_{i}$ is estimable. Thus, $\psi$ is estimable if and only if it is a linear combination of the elements of $\eta = \mathsf E ( \mathbf y )$.

The complication presented by a design matrix $\mathbf{X}$ that is not of full rank may be handled in several ways. First, a re-parametrization with fewer parameters and fewer columns of $\mathbf{X}$ is possible. Second, a popular way is to impose side conditions on the parameters that make them unique. For instance, in the two-way layout (a4) often-used side conditions are: $\sum \alpha _ { i } = 0$, or, equivalently, $\alpha_{.} = 0$ (where dotting on a subscript means averaging over that subscript); similarly, $\beta . = 0$, and $\gamma _ { i } = 0.$ for all $i$, $\gamma _ { j } = 0$ for all $j$. Then all parameters are estimable and (for instance) the hypothesis $\mathcal{H} _ { \text{A} }$ that all main effects of factor $\mathbf{A}$ are $0$ can be expressed by: All $\alpha_i$ are equal to zero. A third way of dealing with an $\mathbf{X}$ of less than full rank is to express all questions of inference in terms of estimable parametric functions. For instance, if in (a4) one writes $\eta _ { i j } = \mu + \alpha _ { i } + \beta _ { j } + \gamma _ { i j }$ ($= \mathsf{E} ( y _ { i j k } )$), then all $\eta_{ij}$ are estimable and $\mathcal{H} _ { \text{A} }$ can be expressed by stating that all $\eta_{ i}.$ are equal, or, equivalently, that all $\eta _ { i .} - \eta _ { - }$ are equal to zero.

Another type of estimator that always exists is a least-squares estimator (LSE; cf. also Least squares, method of). A least-squares estimator of $\beta$ is any vector $\flat$ minimizing $\| \mathbf{y} - \mathbf{Xb} \| ^ { 2 }$. A minimizing $\flat$ (unique if and only if $\mathbf{X}$ is of full rank) is denoted by $\hat{\beta}$ and satisfies the normal equations

\begin{equation} \tag{a5} \mathbf{X} ^ { \prime } \mathbf{X} \widehat { \beta } = \mathbf{X} ^ { \prime } \mathbf{y} . \end{equation}

If $\psi = \mathbf{c} ^ { \prime } \beta$ is estimable, then $\hat { \psi } = \mathbf{c} ^ { \prime } \hat { \beta }$ is unique (even when $\hat{\beta}$ is not) and is called the least-squares estimator of $\psi$. By the Gauss–Markov theorem (cf. also Least squares, method of), $\widehat { \psi }$ is the minimum variance unbiased estimator of $\psi$. See [a48], Sect. 1.4.

A linear hypothesis $\mathcal{H}$ consists of one or more linear restrictions on $\beta$:

\begin{equation} \tag{a6} \mathcal{H} : \mathbf{X} _ { 3 } \beta = 0 \end{equation}

with $\mathbf{X} _ { 3 }$ of order $q \times m$ and rank $q$. Then $\mathcal{H}$ is to be tested against the alternative $\mathbf{X} _ { 3 } \beta \neq 0$. Let $\operatorname{rank} ( \mathbf{X} ) = r$. The model (a1) together with $\mathcal{H}$ of (a6) can be expressed in geometric language as follows: The mean vector $\eta = \mathsf E ( \mathbf y )$ lies in a linear subspace $\Omega$ of $n$-dimensional space, spanned by the columns of $\mathbf{X}$, and $\mathcal{H}$ restricts $ \eta $ to a further subspace $\omega$ of $\Omega$, where $\operatorname { dim } ( \Omega ) = r$ and $\operatorname { dim } ( \omega ) = r - q$. Further analysis is simplified by a transformation to the canonical system, below.

Canonical form.

There is a transformation $\mathbf z = \Gamma \mathbf y $, with $\Gamma$ of order $n \times n$ and orthogonal, so that the model (a1) together with the hypothesis (a6) can be put in the following form (in which $z_1 , \dots ,z_n$ are the elements of $z$ and $\zeta _ { i } = \mathsf{E} ( z _ { i } )$): $z_1 , \dots ,z_n$ are independent, normal, with common variance $\sigma ^ { 2 }$; $\zeta _ { r + 1 } = \ldots = \zeta _ { n } = 0$, and, additionally, $\mathcal{H}$ specifies $\zeta _ { 1 } = \ldots = \zeta _ { q } = 0$. Note that $\zeta _ { q + 1} , \dots , \zeta _ { r }$ are unrestricted throughout. Any estimable parametric function can be expressed in the form $\psi = \sum _ { i = 1 } ^ { r } d _ { i } \zeta _ { i }$, with constants $d_{i}$, and the least-squares estimator of $\psi$ is $\hat { \psi } = \sum _ { i = 1 } ^ { r } d _ { i } z _ { i }$. To estimate $\sigma ^ { 2 }$ one forms the sum of squares for error $\operatorname{SS} _ { e } = \sum _ { i = r + 1 } ^ { n } z _ { i } ^ { 2 }$, and divides by $n - r$ ($=$ degrees of freedom for the error) to form the mean square $\operatorname{MS} _ { e } = \operatorname{SS} _ { e } / ( n - r )$. Then $ \operatorname{MS} _ { e }$ is an unbiased estimator of $\sigma ^ { 2 }$. A test of the hypothesis $\mathcal{H}$ can be obtained by forming $\text{SS} _ { \mathcal{H} } = \sum _ { i = 1 } ^ { q } z _ { i } ^ { 2 }$, with degrees of freedom $q$, and $ \operatorname { MS } _{\mathcal{H}}=\operatorname {SS} _{\mathcal{H}} / q$. Then, if $\mathcal{H}$ is true, the test statistic $\mathcal{F} = \operatorname {MS} _ { \mathcal{H} } / \operatorname {MS}_{\text{e}}$ has an $F$-distribution with degrees of freedom $( q , n - r )$. For a test of $\mathcal{H}$ of level of significance $\alpha$ one rejects $\mathcal{H}$ if $\mathcal{F} > F _ { \alpha ; q , n - r}$ ($=$ the upper $\alpha$-point of the $F$-distribution with degrees of freedom $( q , n - r )$). This is "the" $F$-test; it can be derived as a likelihood-ratio test (LR test) or as a uniformly most powerful invariant test (UMP invariant test) and has several other optimum properties; see [a48], Sect. 2.10. For the power of the $F$-test, see [a48], Sect. 2.8.

Simultaneous confidence intervals.

Let $L$ be the linear space of all parametric functions of the form $\psi = \sum _ { i = 1 } ^ { q } d _ { i } \zeta _ { i }$, i.e., all $\psi$ that are $0$ if $\mathcal{H}$ is true. The $F$-test provides a way to obtain simultaneous confidence intervals for all $\psi \in L$ with confidence level $1 - \alpha$ (cf. also Confidence interval). This is useful, for instance, in cases where $\mathcal{H}$ is rejected. Then any $\psi \in L$ whose confidence interval does not include $0$ is said to be "significantly different from 0" and can be held responsible for the rejection of $\mathcal{H}$. Observe that $q ^ { - 1 } \sum _ { i = 1 } ^ { q } ( z _ { i } - \zeta _ { i } ) ^ { 2 } / \operatorname{MS} _ { e }$ has an $F$-distribution with degrees of freedom $( q , n - r )$ (whether or not $\mathcal{H}$ is true) so that this quantity is $\leq F _ { \alpha ; q , n - \gamma }$ with probability $1 - \alpha$. This inequality can be converted into a family of double inequalities and leads to the simultaneous confidence intervals

\begin{equation} \tag{a7} \mathsf{P} ( \widehat { \psi } - S \widehat { \sigma } _ { \widehat { \psi } } \leq \psi \leq \widehat { \psi } + S \widehat { \sigma } _ { \widehat { \psi } } , \forall \psi \in L ) = 1 - \alpha, \end{equation}

in which $S = ( q F _ { \alpha ; q , n - r } ) ^ { 1 / 2 }$ and $\hat { \sigma }_{ \hat { \psi }} = \| \mathbf{d} \| ( \text{MS} _ { e } ) ^ { 1 / 2 }$ is the square root of the unbiased estimator of the variance $\| \mathbf{d} \| ^ { 2 } \sigma ^ { 2 }$ of $\widehat { \psi } = \sum _ { i = 1 } ^ { q } d _ { i } z _ { i }$. Thus, the confidence interval for $\psi$ has endpoints $\hat { \psi } \pm S \ \hat { \sigma }_{ \hat { \psi }}$, and all $\psi \in L$ are covered by their confidence intervals simultaneously with probability $1 - \alpha$. Note that (a7) is stated without needing the canonical system so that the confidence intervals can be evaluated directly in the original system.

With help of (a7) the $F$-test can also be expressed as follows: $\mathcal{H}$ is accepted if and only if all confidence intervals with endpoints $\hat { \psi } \pm S \ \hat { \sigma }_{ \hat { \psi }}$ cover the value $0$. More generally, it is convenient to make the following definition: a test of a hypothesis $\mathcal{H}$ is exact with respect to a family of simultaneous confidence intervals for a family of parametric functions if $\mathcal{H}$ is accepted if and only if the confidence interval of every $\psi$ in the family includes the value of $\psi$ specified by $\mathcal{H}$; see [a52], [a53]. Thus, the $F$-test is exact with respect to the simultaneous confidence intervals (a7).

The confidence intervals obtained in (a7) are called Scheffé-type simultaneous confidence intervals. Shorter confidence intervals of Tukey-type within a smaller class of parametric functions are possible in some designs. This is applicable, for instance, in the two-way layout of (a4) with equal cell numbers if only differences between the $\alpha_i$ are considered important rather than all parametric functions that are $0$ under $\mathcal{H} _ { \text{A} }$ (so-called contrasts). See [a48], Sect. 3.6.

The canonical system is very useful to derive formulas and prove properties in a unified way, but it is usually not advisable in any given linear model to carry out the transformation $\mathbf z = \Gamma \mathbf y $ explicitly. Instead, the necessary expressions can be derived in the original system. For instance, if $\hat { \eta } \Omega$ and $\widehat { \eta } \omega$ are the orthogonal projections of $\mathbf{y}$ on $\Omega$ and on $\omega$, respectively, then $\operatorname {SS} _ { e } = \| \mathbf{y} - \hat { \eta } _ { \Omega } \| ^ { 2 }$ and $\operatorname {SS} _ { \mathcal H } = \| \widehat { \eta } _ { \Omega } - \widehat { \eta } _ { \omega } \| ^ { 2 }$. These projections can be found by solving the normal equations (a5) (and one gets, for instance, $\hat { \eta } _ { \Omega } = \mathbf{X} \hat { \beta }$), or by minimizing quadratic forms. As an example of the latter: In the two-way layout (a4), minimize $\sum _ { i j k } ( y _ { i j k } - \eta _ { i j } ) ^ { 2 }$ over the $\eta_{ij}$. This yields $\hat { \eta } _ { i j } = y _ { i j }.$, so that $\operatorname{SS} _ { e } = \sum _ { i j k } ( y _ { i j k } - y _ { i j .} ) ^ { 2 }$. If desired, formulas can be expressed in vector and matrix form. As an example, if $\mathbf{X}$ is of maximal rank, then (a5) yields $\hat { \beta } = ( \mathbf{X} ^ { \prime } \mathbf{X} ) ^ { - 1 } \mathbf{X} ^ { \prime } \mathbf{y}$ and $\operatorname {SS} _ { e } = \mathbf{y} ^ { \prime } ( \mathbf{I} _ { n } - \mathbf{X} ( \mathbf{X} ^ { \prime } \mathbf{X} ) ^ { - 1 } \mathbf{X} ^ { \prime } ) \mathbf{y}$. Similar expressions hold under $\mathcal{H}$ after replacing $\mathbf{X}$ by a matrix whose columns span $\omega$. If $\mathbf{X}$ is not of maximal rank, then a generalized inverse may be employed. See [a43], Sect. 4a.3, and [a45].

MANOVA.

There are several good textbooks on multivariate analysis that treat various aspects of MANOVA. Among the major ones are [a1], [a8], [a19], [a29], [a36], [a41], and [a43], Chap. 8. See also [a56], headings Multivariate Analysis; Multivariate Analysis Of Variance, and [a14]. The ideas involved in MANOVA are essentially the same as in ANOVA, but there is an added dimension in that the observations are now multivariate. For instance, if measurements are made on $p$ different features of the same individual, then this should be regarded as one observation on a $p$-variate distribution. The MANOVA model is given by (a2). A linear hypothesis on $\mathbf{B}$ analogous to (a6) is

\begin{equation} \tag{a8} \mathcal{H} : \mathbf{X} _ { 3 } \mathbf{B} = 0, \end{equation}

with $\mathbf{X} _ { 3 }$ as in (a6). Any ANOVA testing problem defined by the choice of $\mathbf{X}$ in (a1) and $\mathbf{X} _ { 3 }$ in (a6) carries over to the same kind of problem given by (a2) and (a8). However, since $\mathbf{B}$ is a matrix, there are other ways than (a8) of formulating a linear hypothesis. The most obvious extension of (a8) is

\begin{equation} \tag{a9} \mathcal {H} : {\bf X} _ { 3 } {\bf B X} _ { 4 } = 0, \end{equation}

in which $\mathbf{X}_{4}$ is a known $( p \times p _ { 1 } )$-matrix of rank $p _ { 1 }$. However, (a9) can be reduced to (a8) by making the transformation $\mathbf{Z} = \mathbf{Y X}_4$, of order $n \times p _ { 1 }$, $\Gamma = \mathbf{B} \mathbf{X}_4$, $\mathbf{F} = \mathbf{EX}_4$; then the model is ${\bf Z = X} \Gamma + \bf F$, with the rows of $\mathbf{F}$ independent identically distributed $N ( 0 , \Sigma _ { 1 } )$, $\Sigma _ { 1 } = \mathbf{X} _ { 4 } ^ { \prime } \Sigma \mathbf{X} _ { 4 }$, and $\mathcal{H} : \mathbf{X} _ { 3 } \Gamma = 0$. Thus, the transformed problem is as (a2), (a8), with $\mathbf{Z} , \Gamma , \mathbf{F}$ replacing $\mathbf{Y} , \mathbf{B} , \mathbf{E}$. This can be applied, for instance, to profile analysis; see [a29], Sect. 5.4 (A5), [a36], Sects. 4.6, 5.6.

There is a canonical form of the MANOVA testing problem (a2), (a8) analogous to the ANOVA problem (a1), (a6), the difference being that the real-valued random variables $z_i$ of ANOVA are replaced by $1 \times p$ random vectors. These vectors form the rows of three random matrices, $\mathbf{Z} _ { 1 }$ of order $q \times p$, $\mathbf{Z}_{2}$ of order $( r - q ) \times p$, and $\mathbf{Z}_{3}$ of order $( n - r ) \times p$, all of whose rows are assumed independent and $p$-variate normal with common non-singular covariance matrix $\Sigma$; furthermore, $\mathsf{E} ( \mathbf{Z} _ { 3 } ) = 0$, $\mathsf{E} ( \mathbf Z _ { 2 } )$ is unspecified, and $\mathcal{H}$ specifies $\mathsf{E} ( {\bf Z} _ { 1 } ) = 0$. It is assumed that $n - r \geq p$. Put $\mathsf E ( \mathbf Z _ { 1 } ) = \Theta$, so that $\mathbf{Z} _ { 1 }$ is an unbiased estimator of $\Theta$. For testing $\mathcal{H} : \Theta = 0$, $\mathbf{Z}_{2}$ is ignored and the sums of squares $\text{SS} _ { \mathcal{H} }$ and $\text{SS} _ { e }$ of ANOVA are replaced by the $( p \times p )$-matrices $\mathbf{M} _ { \mathcal{H} } = \mathbf{Z} _ { 1 } ^ { \prime }\mathbf{ Z} _ { 1 }$ and $\mathbf{M} _ { \mathsf{E} } = \mathbf{Z} _ { 3 } ^ { \prime } \mathbf{Z} _ { 3 }$, respectively. An application of sufficiency plus the principle of invariance restricts tests of $\mathcal{H}$ to those that depend only on the positive characteristic roots of $\mathbf{M} _ { \mathcal{H} } \mathbf{M} _ { \mathsf{E} } ^ { - 1 }$ ($=$ the positive characteristic roots of $\mathbf{Z} _ { 1 } \mathbf{M} _ { \mathsf{E} } ^ { - 1 } \mathbf{Z} _ { 1 } ^ { \prime }$). The case $q = 1$, when $\mathbf{Z} _ { 1 }$ is a row vector, deserves special attention. It arises, for instance, when testing for zero mean in a single multivariate population or testing the equality of means in two such populations. Then $F = \mathbf{Z} _ { 1 } \mathbf{M} _ { \mathsf{E} } ^ { - 1 } \mathbf{Z} _ { 1 } ^ { \prime }$ is the only positive characteristic root; $( n - r ) F$ is called Hotelling's $T ^ { 2 }$, and $p ^ { - 1 } ( n - r - p + 1 ) F$ has an $F$-distribution with degrees of freedom $( p , n - r - p + 1 )$, central or non-central according as $\mathcal{H}$ is true or false. Rejecting $\mathcal{H}$ for large values of $F$ is uniformly most powerful invariant. If $q \geq 2$ there is no best way of combining the $q$ characteristic roots, so that there is no uniformly most powerful invariant test (unlike there is in ANOVA). The following tests have been proposed:

reject $\mathcal{H}$ if 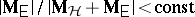(Wilks LR test);

reject $\mathcal{H}$ if the largest characteristic root of $\mathbf{M} _ { \mathcal{H} } \mathbf{M} _ { \mathsf{E} } ^ { - 1 }$ exceeds a constant (Roy's test);

reject $\mathcal{H}$ if $\operatorname{tr}( \mathbf{M} _ { \mathcal{H} } \mathbf{M} _ { \mathsf{E} } ^ { - 1 } ) > \text{const}$ (Lawley–Hotelling test);

reject $\mathcal{H}$ if $\operatorname { tr } ( \mathbf{M} _ { \mathcal{H} } ( \mathbf{M} _ { H } + \mathbf{M} _ { \mathsf{E} } ) ^ { - 1 } ) > \text{const}$ (Bartlett–Nanda–Pillai test). For references, see [a1], Sects. 8.3, 8.6, or [a36], Chap. 5. For distribution theory, see [a1], Sects. 8.4, 8.6, [a41], Sects. 10.4–10.6, [a55], Sect. 10.3. Tables and charts can be found in [a1], Appendix, and [a36], Appendix.

The problem of expressing the matrices $\mathbf{M} _ { \mathcal{H} }$ and ${\bf M} _ { \mathsf{E} }$ in terms of the original model given by (a2), (a8) is very similar to the situation in ANOVA. One way is to express $\mathbf{M} _ { \mathcal{H} }$ and ${\bf M} _ { \mathsf{E} }$ explicitly in terms of $\mathbf{X}$ and $\mathbf{X} _ { 3 }$. Another is to consider the ANOVA problem with the same $\mathbf{X}$ and $\mathbf{X} _ { 3 }$; if explicit formulas exist for $\text{SS} _ { \mathcal{H} }$ and $\text{SS} _ { e }$, they can be converted to $\mathbf{M} _ { \mathcal{H} }$ and ${\bf M} _ { \mathsf{E} }$. For instance, $\operatorname{SS} _ { e } = \sum _ { i j k } ( y _ { i j k } - y _ { i j .} ) ^ { 2 }$ in the ANOVA two-way layout (a4) converts to $\mathbf{M} _ { \mathsf{E} } = \sum _ { i j k } ( \mathbf{y} _ { i j k } - \mathbf{y} _ { i j }. ) ^ { \prime } ( \mathbf{y} _ { i j k } - \mathbf{y} _ { i j }. )$ in the corresponding MANOVA problem, where now the $\mathbf{y} _ { i j k }$ are $( 1 \times p )$-vectors.

Point estimation.

In the canonical system $\mathbf{Z} _ { 1 }$ is an unbiased estimator and the maximum-likelihood estimator of $\Theta$ (cf. also Maximum-likelihood method). If $f$ is a linear function of $\Theta$, then $f ( \mathbf{Z} _ { 1 } )$ is both an unbiased estimator and a maximum-likelihood estimator of $f ( \Theta )$. An unbiased estimator of $\Sigma$ is 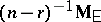, whereas its maximum-likelihood estimator is $n ^ { - 1 } \mathbf{M} _ { \mathsf{E} }$.

Confidence intervals and sets.

There are several kinds of linear functions of $\Theta$ that are of interest. The direct analogue of a linear function of $\zeta _ { 1 } , \ldots , \zeta _ { q }$ in ANOVA is a function of the form $\mathbf{a} ^ { \prime } \Theta$ (with $\mathbf{a}$ of order $q \times 1$), which is a $( 1 \times p )$-vector. This leads to a confidence set in $p$-space for $\mathbf{a} ^ { \prime } \Theta$, rather than an interval. Simultaneous confidence sets for all $\mathbf{a} ^ { \prime } \Theta$ can be derived from any of the proposed tests for $\mathcal{H}$, but it turns out that only Roy's maximum root test is exact with respect to these confidence sets (and not, for instance, the LR test of Wilks); see [a52], [a53]. The same is true for simultaneous confidence sets for all $\Theta \mathbf{b}$, and confidence intervals for all $\mathbf{a} ^ { \prime } \Theta \mathbf b $. Simultaneous confidence sets for all $\mathbf{a} ^ { \prime } \Theta$ were given in [a18]. In [a46] simultaneous confidence intervals for all $\mathbf{a} ^ { \prime } \Theta \mathbf b $ are derived (called "double linear compounds" ). These are special cases of all (possibly matrix-valued) functions of the form $\mathbf{A} \Theta \mathbf{B}$ are treated in [a11]. The most general linear functions of $\Theta$ are of the form $\operatorname { tr } ( \mathbf{N} \Theta )$. Simultaneous confidence intervals for all such functions as $\mathbf{N}$ runs through all $( p \times q )$-matrices are given in [a37]. These are derived from a test defined in terms of a symmetric gauge function rather than from Roy's maximum root test. In [a52], [a53] a generalization of this is given if $\mathbf{N}$ has its rank restricted; for $\operatorname{rank}( \mathbf{N}) \leq 1$ this reproduces the confidence intervals of [a46].

Step-down procedures.

Partition $\mathbf{B}$ into its columns $\beta _ { 1 } , \ldots , \beta _ { p }$; then $\mathcal{H}$ of (a8) is the intersection of the component hypotheses $\mathcal{H} _ { j } : \mathbf{X} _ { 3 } \beta _ { j } = 0$. Also partition $\mathbf{Y}$ into its columns ${\bf y} _ { 1 } , \dots , {\bf y} _ { p }$. Then for each $j = 1 , \ldots , p$, the hypothesis ${\cal H} _ { j }$ is tested with a univariate ANOVA $F$-test that depends only on ${\bf y} _ { 1 } , \dots , {\bf y} _ { j }$. If any ${\cal H} _ { j }$ is rejected, then $\mathcal{H}$ is rejected. The tests are independent, which permits easy determination of the overall level of significance in terms of the individual ones. For details, history of the subject and references, see [a38] and [a39], Sect. 3. A variation, based on $P$-values, is presented in [a40]. Step-down procedures are convenient, but it is shown in [a34] that even in the simplest case when $q = 1$, a step-down test is not admissible. Furthermore, a step-down test is not exact with respect to simultaneous confidence intervals or confidence sets derived from the test for various linear functions of $\mathbf{B}$; see [a53], Sect. 4.4. A generalization of step-down procedures is proposed in [a38] by grouping the column vectors of $\mathbf{Y}$ and $\mathbf{B}$ into blocks.

Random effects models.

Some references on this topic in MANOVA are [a2] and [a35]; see also references quoted therein.

Missing data.

Statistical experiments involving multivariate observations bring in an element that is not present with univariate observations, such as in ANOVA. Above, it has been taken for granted that of every individual in a sample all $p$ variates are observed. In practice this is not always true, for various reasons, in which case some of the observations have missing data. (This is not to be confused with the notion of empty cells in ANOVA.) If that happens, one can group all observations with complete data together as the complete sample and call the remaining observations an incomplete sample. From a slightly different point of view, the incomplete sample is sometimes considered extra data on some of the variates. The analysis of MANOVA problems is more complicated when there are missing data. In the simplest case, all missing data are on the same variates. This is a special case of nested missing data patterns. In the latter case explicit expressions of maximum-likelihood estimators are possible; see [a3] and the references therein. For more complicated missing data patterns explicit maximum-likelihood estimators are usually not available unless certain assumptions are made on the structure of the unknown covariance matrix $\Sigma$; see [a3], [a4] and [a5]. The situation is even worse for testing. For instance, even in the simplest case of testing the hypothesis that the mean of a multivariate population is $0$, if in addition to a complete sample there is an incomplete one taken on a subset of the variates, then there is no locally (let alone uniformly) most-powerful test; see [a9]. Several aspects of estimation and testing in the presence of various patterns of missing data can be found in [a25], wherein also appear many references to other papers in the field.

GMANOVA.

This topic has not been recognized as a distinct entity within multivariate analysis until relatively recently. Consequently, most of today's (2000) knowledge of the subject is found in the research literature, rather than in textbooks. (There is an introduction to GMANOVA in [a41], Problem 10.18, and a little can be found in [a8], Sect. 9.6, second part.) A good exposition of testing aspects of GMANOVA, pointing to applications in various experimental settings, is given in [a21].

The general GMANOVA model was first stated in [a42], where the motivation was the modelling of experiments on the comparison of growth curves in different populations. Suppose such a growth curve can be represented by a polynomial in the time $t$, say $f ( t ) = \beta _ { 0 } + \beta _ { 1 } t + \ldots + \beta _ { k } t ^ { k }$. If measurements are made on an individual at times $t _ { 1 } , \ldots , t _ { p }$, then these $p$ data are thought of as one observation on a $p$-variate population with population mean $( f ( t _ { 1 } ) , \ldots , f ( t _ { p } ) )$ and covariance matrix $\Sigma$, where the $\beta$s and $\Sigma$ are unknown parameters. Suppose $m$ populations are to be compared and a sample of size $n_i$ is taken from the $i$th population, $i = 1 , \ldots , m$. In order to model this by (a3), let the $i$th column of $\mathbf{X} _ { 1 }$ (corresponding to the $i$th population) have $n_i$ $1$s, and $0$s otherwise. Specifically, the first column has a $1$ in positions $1 , \ldots , n _ { 1 }$, the second in positions $n _ { 1 } + 1 , \ldots , n _ { 1 } + n _ { 2 }$, etc.; then $n = \sum n_{i}$. Let the growth curve in the $i$th population be $\beta _ { i 0 } + \beta _ { i 1 } t + \ldots + \beta _ { i k } t ^ { k }$; then the matrix $\mathbf{B}$ has $m$ rows, the $i$th row being $( \beta _ { i 0 } , \ldots , \beta _ { i k } )$, so that $s = k + 1$ in (a3); and $\mathbf{X} _ { 2 }$ has $p$ columns, the $j$th one being $( 1 , t _ { j } , \ldots , t _ { j } ^ { k } ) ^ { \prime }$. (In the example given in [a42], measurements were taken at ages 8, 10, 12, and 14 in a group of girls and a group of boys; each measurement was of a certain distance between two points inside the head (with help of an X-ray picture) that is of interest in orthodontistry to monitor growth.)

Linear hypotheses are in general of the form (a9). For instance, suppose two growth curves are to be compared, both assumed to be straight lines ($k = 1$) so that $m = 2$, $s = 2$. Suppose the hypothesis is $\beta _ { 11 } = \beta _ { 21 }$ (equal slope in the two populations). Then in (a9) one can take $\mathbf{X} _ { 3 } = ( 1 , - 1 )$ and $\mathbf{X} _ { 4 } = ( 0,1 ) ^ { \prime }$. Other examples of GMANOVA may be found in [a21].

A canonical form for the GMANOVA model was derived in [a13]; it can also be found in [a21], Sect. 3.2. It can be obtained from the canonical form of MANOVA by partitioning the matrices $\mathbf{Z}_{i}$ columnwise into three blocks, resulting in $9$ matrices ${\bf Z} _ { i j }$, $i, j = 1,2,3$. Invariance reduction eliminates all ${\bf Z} _ { i j }$ except $[ \mathbf{Z} _ { 12 } , \mathbf{Z} _ { 13 } ]$ and $[\mathbf{Z} _ { 32 } , \mathbf{Z} _ { 33 }]$ (the latter is used for estimating the relevant portion of the unknown covariance matrix $\Sigma$). It is given that $\mathsf{E} ( {\bf Z} _ { 13 } ) = 0$ and $\mathsf E [ \mathbf Z _ { 32 } , \mathbf Z _ { 33 } ] = 0$; inference is desired on $\Theta = \textsf{E} ( \mathbf{Z} _ { 12 } )$, e.g., to test the hypothesis $\mathcal{H} : \Theta = 0$. Further sufficiency reduction leads to two matrix-valued statistics $\mathbf{T} _ { 1 }$ and $\mathbf{T} _ { 2 }$ ([a20], [a21]), of which $\mathbf{T} _ { 1 }$ is the most important and is built-up from the following statistic:

\begin{equation} \tag{a10} \mathbf{Z} _ { 0 } = \mathbf{Z} _ { 12 } - \mathbf{Z} _ { 13 } \mathbf{R}, \end{equation}

in which $\mathbf{R} = \mathbf{V} _ { 33 } ^ { - 1 } \mathbf{V} _ { 32 }$ (with ${\bf V} _ { j j ^ { \prime } } = {\bf Z} _ { 3 j } ^ { \prime } {\bf Z} _ { 3 j^{\prime} }$) is the estimated regression of $\mathbf{Z} _ { 12 }$ on $\mathbf{Z} _ { 13 }$, the true regression being $\Sigma _ { 33 } ^ { - 1 } \Sigma _ { 32 }$. That inference on $\Theta$ should be centred on $\mathbf{Z}_{0}$ can be understood intuitively by realizing that if $\Sigma$ were known, then $\mathbf{Z} _ { 12 } - \mathbf{Z} _ { 13 } \Sigma _ { 33 } ^ { - 1 } \Sigma _ { 32 }$ minimizes the variances among all linear combinations of $\mathbf{Z} _ { 12 }$ and $\mathbf{Z} _ { 13 }$ whose mean is $\Theta$, and provides therefore better inference than using only $\mathbf{Z} _ { 12 }$. The unknown regression is then estimated by $\mathbf{R}$, leading to $\mathbf{Z}_{0}$ of (a10).

The essential difference between GMANOVA and MANOVA lies in the presence of $\mathbf{Z} _ { 13 }$, which is correlated with $\mathbf{Z} _ { 12 }$ and has zero mean. Then $\mathbf{Z} _ { 13 }$ is used as a covariate for $\mathbf{Z} _ { 12 }$; see, e.g., [a33]. However, not all models that appear to be GMANOVA produce such a covariate. More precisely, if in (a3) $\operatorname{rank} (\mathbf{X} _ { 2 } ) = p$, then it turns out that in the canonical form there are no matrices ${\bf Z} _ { i3 }$ and the model reduces essentially to MANOVA. This situation was encountered previously when it was pointed out that the MANOVA model (a2) together with the GMANOVA-type hypothesis (a9) was immediately reducible to straight MANOVA. The same conclusion would have been reached after treating (a2), (a9) as a special case of GMANOVA and inspecting the canonical form. For a "true" GMANOVA the existence of $\mathbf{Z} _ { 13 }$ is essential. A typical example of true GMANOVA, where the covariate data are built into the experiment, was given in [a7].

Inference on $\Theta$ can proceed using only $\mathbf{T} _ { 1 }$ (e.g., [a27], and [a13]), but is not necessarily the best possible. For testing $\mathcal{H}$ an essentially complete class of tests include those that also involve $\mathbf{T} _ { 2 }$ explicitly. One such test is the locally most-powerful test derived in [a20]. For the distribution theory of $( \mathbf{T} _ { 1 } , \mathbf{T} _ { 2 } )$ see [a21], Sect. 3.6, and [a54], Sect. 6.5. Admissibility and inadmissibility results were obtained in [a32]; comparison of various tests can also be found there. A natural estimator of $\Theta$ is $\mathbf{Z}_{0}$ of (a10); it is an unbiased estimator and in [a22] it is shown to be best equivariant. Other kinds of estimators have also been considered, e.g., in [a24], in which several references to earlier work can be found. Simultaneous confidence intervals and sets have been treated in [a16], [a17], [a27], and [a28]. Special structures of the covariance matrix $\Sigma$ have been studied in [a44], where also references to earlier work on related topics can be found.

Generalizations.

A natural generalization of the GMANOVA model is indicated in [a13] by having a further partitioning of the blocks of $Z$s in the canonical form. This is called extended GMANOVA in [a21] and examples are given there. Another generalization involves some relaxation of the usual assumptions of multivariate normality, etc. See [a23], [a12], [a17].

References

[a1]	T.W. Anderson, "An introduction to multivariate statistical analysis" , Wiley (1984) (Edition: Second) MR0771294 Zbl 0651.62041
[a2]	T.W. Anderson, "The asymptotic distribution of characteristic roots and vectors in multivariate components of variance" L.J. Gleser (ed.) M.D. Perlman (ed.) S.J. Press (ed.) A.R. Sampson (ed.) , Contributions to Probability and Statistics; Essays in Honor of Ingram Olkin , Springer (1989) pp. 177–196 MR1024331
[a3]	S.A. Andersson, M.D. Perlman, "Lattice-ordered conditional independence models for missing data" Statist. Prob. Lett. , 12 (1991) pp. 465–486 MR1143745 Zbl 0751.62026
[a4]	S.A. Andersson, M.D. Perlman, "Lattice models for conditional independence in a multivariate normal distribution" Ann. Statist. , 21 (1993) pp. 1318–1358 MR1241268 Zbl 0803.62042
[a5]	S.A. Andersson, J.I. Marden, M.D. Perlman, "Totally ordered multivariate linear models" Sankhyā A , 55 (1993) pp. 370–394 MR1323395
[a6]	Y.M.M. Bishop, S.E. Fienberg, P.W. Holland, "Discrete multivariate analysis: Theory and practice" , MIT (1975) MR0381130 Zbl 0332.62039
[a7]	W.G. Cochran, C.I. Bliss, "Discrimination functions with covariance" Ann. Statist. , 19 (1948) pp. 151–176
[a8]	M.L. Eaton, "Multivariate statistics, a vector space approach" , Wiley (1983) Zbl 0587.62097
[a9]	M.L. Eaton, T. Kariya, "Multivariate tests with incomplete data" Ann. Statist. , 11 (1983) pp. 654–665 MR0696076 Zbl 0524.62051
[a10]	S.E. Fienberg, "The analysis of cross-classified categorical data" , MIT (1980) (Edition: Second) MR0623082 Zbl 0499.62049
[a11]	K.R. Gabriel, "Simultaneous test procedures in multivariate analysis of variance" Biometrika , 55 (1968) pp. 489–504 MR0235667
[a12]	N. Giri, K. Das, "On a robust test of the extended MANOVA problem in elliptically symmetric distributions" Sankhyā A , 50 (1988) pp. 234–248
[a13]	L.J. Gleser, I. Olkin, "Linear models in multivariate analysis" R.C. Bose (ed.) , Essays in Probability and Statistics: In memory of S.N. Roy , Univ. North Carolina Press (1970) pp. 267–292 MR0267693
[a14]	"Analysis of Variance" P.R. Krishnaiah (ed.) , Handbook of Statistics , 1 , North-Holland (1980) MR0600318 Zbl 0447.00013
[a15]	K. Hinkelmann, O. Kempthorne, "Design and analysis of experiments" , I: Introduction to experimental design , Wiley (1994) MR1265939 Zbl 0805.62071
[a16]	P.M. Hooper, "Simultaneous interval estimation in the general multivariate analysis of variance model" Ann. Statist. , 11 (1983) pp. 666–673 (Correction in: 12 (1984), 785) MR0696077 MR0740934 Zbl 0526.62032
[a17]	P.M. Hooper, W.K. Yau, "Optimal confidence regions in GMANOVA" Canad. J. Statist. , 14 (1986) pp. 315–322 MR0876757 Zbl 0625.62021
[a18]	D.R. Jensen, L.S. Mayer, "Some variational results and their applications in multiple inference" Ann. Statist. , 5 (1977) pp. 922–931 MR0448707 Zbl 0368.62007
[a19]	R.A. Johnson, D.W. Wichern, "Applied multivariate statistical analysis" , Prentice-Hall (1988) (Edition: Second) MR2372475 MR1168210 MR0653327 Zbl 0663.62061
[a20]	T. Kariya, "The general MANOVA problem" Ann. Statist. , 6 (1978) pp. 200–214 MR0474629 Zbl 0382.62042
[a21]	T. Kariya, "Testing in the multivariate general linear model" , Kinokuniya (1985)
[a22]	T. Kariya, "Equivariant estimation in a model with an ancillary statistic" Ann. Statist. , 17 (1989) pp. 920–928 MR0994276 Zbl 0697.62020
[a23]	T. Kariya, B.K. Sinha, "Robustness of statistical tests" , Acad. Press (1989) MR0996634 Zbl 0699.62033
[a24]	T. Kariya, Y. Konno, W.E. Strawderman, "Double shrinkage estimators in the GMANOVA model" J. Multivar. Anal. , 56 (1996) pp. 245–258 MR1379529 Zbl 0863.62055
[a25]	T. Kariya, P.R. Krishnaiah, C.R. Rao, "Statistical inference from multivariate normal populations when some data is missing" P.R. Krishnaiah (ed.) , Developm. in Statist. , 4 , Acad. Press (1983) pp. 137–148
[a26]	O. Kempthorne, "The design and analysis of experiments" , Wiley (1952) MR1528291 MR0045368 Zbl 0049.09901
[a27]	C.G. Khatri, "A note on a MANOVA model applied to problems in growth curves" Ann. Inst. Statist. Math. , 18 (1966) pp. 75–86 MR0219181
[a28]	P.R. Krishnaiah, "Simultaneous test procedures under general MANOVA models" P.R. Krishnaiah (ed.) , Multivariate Analysis II , Acad. Press (1969) pp. 121–143 MR254975
[a29]	A.M. Kshirsagar, "Multivariate analysis" , M. Dekker (1972) MR0343478 Zbl 0246.62064
[a30]	E.L. Lehmann, "Theory of point estimation" , Wiley (1983) MR0702834 Zbl 0522.62020
[a31]	E L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) (Edition: Second) MR0852406 Zbl 0608.62020
[a32]	J.I. Marden, "Admissibility of invariant tests in the general multivariate analysis of variance problem" Ann. Statist. , 11 (1983) pp. 1086–1099 MR0720255 Zbl 0598.62006
[a33]	J.I. Marden, M.D. Perlman, "Invariant tests for means with covariates" Ann. Statist. , 8 (1980) pp. 25–63 MR0557553 Zbl 0454.62049
[a34]	J.I. Marden, M.D. Perlman, "On the inadmissibility of step-down procedures for the Hotelling ${\bf T} ^ { 2 }$ problem" Ann. Statist. , 18 (1990) pp. 172–190 MR1041390 Zbl 0712.62052
[a35]	T. Mathew, A. Niyogi, B.K. Sinha, "Improved nonnegative estimation of variance components in balanced multivariate mixed models" J. Multivar. Anal. , 51 (1994) pp. 83–101 MR1309370 Zbl 0806.62057
[a36]	D.F. Morrison, "Multivariate statistical methods" , McGraw-Hill (1976) (Edition: Second) MR0408108 Zbl 0355.62049
[a37]	G.S. Mudholkar, "On confidence bounds associated with multivariate analysis of variance and non-independence between two sets of variates" Ann. Math. Statist. , 37 (1966) pp. 1736–1746 MR0214204 Zbl 0146.40403
[a38]	G.S. Mudholkar, P. Subbaiah, "A review of step-down procedures for multivariate analysis of variance" R.P. Gupta (ed.) , Multivariate Statistical Analysis , North-Holland (1980) pp. 161–178 MR0600149 Zbl 0445.62079
[a39]	G.S. Mudholkar, P. Subbaiah, "Some simple optimum tests in multivariate analysis" A.K. Gupta (ed.) , Advances in Multivariate Statistical Analysis , Reidel (1987) pp. 253–275
[a40]	G.S. Mudholkar, P. Subbaiah, "On a Fisherian detour of the step-down procedure for MANOVA" Commun. Statist. Theory and Methods , 17 (1988) pp. 599–611 MR0939669 Zbl 0665.62056
[a41]	R.J. Muirhead, "Aspects of multivariate statistical theory" , Wiley (1982) MR0652932 Zbl 0556.62028 Zbl 0678.62065
[a42]	R.F. Potthoff, S.N. Roy, "A generalized multivariate analysis of variance model useful especially for growth curve models" Biometrika , 51 (1964) pp. 313–326
[a43]	C.R. Rao, "Linear statistical inference and its applications" , Wiley (1973) (Edition: Second) MR0346957 Zbl 0256.62002
[a44]	C.R. Rao, "Least squares theory using an estimated dispersion matrix and its application to measurement of signals" L.M. Le Cam (ed.) J. Neyman (ed.) , Fifth Berkeley Symp. Math. Statist. Probab. , 1 , Univ. California Press (1967) pp. 355–372 MR0212930 Zbl 0189.18503
[a45]	C.R. Rao, S.K. Mitra, "Generalized inverses of matrices and its applications" , Wiley (1971) MR0338013 MR0321249
[a46]	S.N. Roy, R.C. Bose, "Simultaneous confidence interval estimation" Ann. Math. Statist. , 24 (1953) pp. 513–536 MR0060781 Zbl 0052.15403
[a47]	H. Scheffé, "Alternative models for the analysis of variance" Ann. Math. Statist. , 27 (1956) pp. 251–271 MR0082249 Zbl 0072.36602
[a48]	H. Scheffé, "The analysis of variance" , Wiley (1959) MR0116429 Zbl 0086.34603
[a49]	S.R. Searle, "Linear models" , Wiley (1971) MR0293792 Zbl 0218.62071
[a50]	S.R. Searle, "Linear models for unbalanced data" , Wiley (1987) MR0907471 Zbl 1095.62080
[a51]	S. Weisberg, "Applied linear regression" , Wiley (1985) (Edition: Second) MR2112740 MR0591462 Zbl 0646.62058
[a52]	R.A. Wijsman, "Constructing all smallest simultaneous confidence sets in a given class, with applications to MANOVA" Ann. Statist. , 7 (1979) pp. 1003–1018 MR0536503 Zbl 0416.62030
[a53]	R.A. Wijsman, "Smallest simultaneous confidence sets with applications in multivariate analysis" P.R. Krishnaiah (ed.) , Multivariate Analysis V , North-Holland (1980) pp. 483–498 MR0566358 Zbl 0431.62031
[a54]	R.A. Wijsman, "Global cross sections as a tool for factorization of measures and distribution of maximal invariants" Sankhyā A , 48 (1986) pp. 1–42 MR0883948 Zbl 0618.62006
[a55]	R.A. Wijsman, "Invariant measures on groups and their use in statistics" , Lecture Notes Monograph Ser. , 14 , Inst. Math. Statist. (1990) MR1218397 Zbl 0803.62001
[a56]	"Encyclopedia of Statistical Sciences" S. Kotz (ed.) N.L. Johnson (ed.) , Wiley (1982/88) MR1679440 MR1605063 MR1469744 MR1044999 MR0976457 MR0976456 MR0892738 MR0873585 MR0793593 MR0719029 MR0719028 MR0670950 MR0646617 Zbl 1136.62001 Zbl 0919.62001 Zbl 0897.62002 Zbl 0897.62001 Zbl 0727.62001 Zbl 0706.62002 Zbl 0657.62003 Zbl 0657.62002 Zbl 0657.62001 Zbl 0585.62002 Zbl 0585.62001 Zbl 0552.62001