Difference between revisions of "Two-dimensional annulus"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | t0945001.png | ||
| + | $#A+1 = 29 n = 6 | ||
| + | $#C+1 = 29 : ~/encyclopedia/old_files/data/T094/T.0904500 Two\AAhdimensional annulus | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''in topology'' | ''in topology'' | ||
A topological image of the closed part of the plane comprised between two non-identical concentric circles. A two-dimensional annulus is an orientable [[Two-dimensional manifold|two-dimensional manifold]] of genus zero with two boundary components. | A topological image of the closed part of the plane comprised between two non-identical concentric circles. A two-dimensional annulus is an orientable [[Two-dimensional manifold|two-dimensional manifold]] of genus zero with two boundary components. | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Thus, a | + | Thus, a $ 2 $- |
| + | dimensional annulus is homeomorphic to $ S ^ {1} \times I $, | ||
| + | where $ S ^ {1} $ | ||
| + | is the circle and $ I $ | ||
| + | the interval. An $ n $- | ||
| + | dimensional annulus is a space homeomorphic to $ S ^ {n-} 1 \times I $. | ||
| + | The $ n $- | ||
| + | dimensional annulus conjecture states that for any homeomorphism $ h: \mathbf R ^ {n} \rightarrow \mathbf R ^ {n} $ | ||
| + | such that $ h( B ^ {n} ) \subset \mathop{\rm Int} ( B ^ {n} ) $, | ||
| + | the interior of $ B ^ {n} $, | ||
| + | the closed difference | ||
| − | + | $$ | |
| + | B ^ {n} \setminus h( \mathop{\rm Int} ( B ^ {n} )) | ||
| + | $$ | ||
| − | is homeomorphic to the annulus | + | is homeomorphic to the annulus $ S ^ {n-} 1 \times I $. |
| + | Here, $ B ^ {n} = \{ {x \in \mathbf R ^ {n} } : {\| x \| \leq 1 } \} $. | ||
| − | The stable homeomorphism conjecture asserts that any orientation-preserving homeomorphism | + | The stable homeomorphism conjecture asserts that any orientation-preserving homeomorphism $ h: \mathbf R ^ {n} \rightarrow \mathbf R ^ {n} $ |
| + | can be written as a finite product, $ h = h _ {1} \dots h _ {m} $, | ||
| + | where each $ h _ {i} $ | ||
| + | is the identity on some open subset of $ \mathbf R ^ {n} $. | ||
| − | The stable homeomorphism conjecture for dimension | + | The stable homeomorphism conjecture for dimension $ n $ |
| + | implies the annulus conjecture for dimension $ n $. | ||
| − | The stable homeomorphism conjecture (and hence the annulus conjecture) has finally been established for all | + | The stable homeomorphism conjecture (and hence the annulus conjecture) has finally been established for all $ n $: |
| + | $ n= 1 $, | ||
| + | classical; $ n= 2 $, | ||
| + | [[#References|[a6]]]; $ n= 3 $, | ||
| + | ; $ n \geq 5 $, | ||
| + | [[#References|[a3]]]; and, finally, $ n= 4 $, | ||
| + | [[#References|[a2]]], as an application of a special controlled [[H-cobordism| $ h $- | ||
| + | cobordism]] theorem in dimension $ 5 $, | ||
| + | called the thin $ h $- | ||
| + | cobordism theorem or Quinn's thin $ h $- | ||
| + | cobordism theorem. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.D. Edwards, "The solution of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094500/t09450033.png" />-dimensional annulus conjecture (after Frank Quinn)" ''Contemporary Math.'' , '''35''' (1984) pp. 211–264</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> F. Quinn, "Ends of maps III: dimensions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094500/t09450034.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094500/t09450035.png" />" ''J. Diff. Geom.'' , '''17''' (1982) pp. 503–521</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R. Kirby, "Stable homeomorphisms and the annulus conjecture" ''Ann. of Math.'' , '''89''' (1969) pp. 575–582</TD></TR><TR><TD valign="top">[a4a]</TD> <TD valign="top"> E.E. Moise, "Affine structures in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094500/t09450036.png" />-manifolds I" ''Ann. of Math.'' , '''54''' (1951) pp. 506–533</TD></TR><TR><TD valign="top">[a4b]</TD> <TD valign="top"> E.E. Moise, "Affine structures in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094500/t09450037.png" />-manifolds II, III" ''Ann. of Math.'' , '''55''' (1952) pp. 172–176; 203–222</TD></TR><TR><TD valign="top">[a4c]</TD> <TD valign="top"> E.E. Moise, "Affine structures in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094500/t09450038.png" />-manifolds IV" ''Ann. of Math.'' , '''56''' (1952) pp. 96–114</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> M. Brown, H. Gluck, "Stable structures on manifolds I-III" ''Ann. of Math.'' , '''79''' (1974) pp. 1–58</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> T. Radó, "Über den Begriff der Riemannsche Fläche" ''Acta Univ. Szeged'' , '''2''' (1924–1926) pp. 101–121</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.D. Edwards, "The solution of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094500/t09450033.png" />-dimensional annulus conjecture (after Frank Quinn)" ''Contemporary Math.'' , '''35''' (1984) pp. 211–264</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> F. Quinn, "Ends of maps III: dimensions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094500/t09450034.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094500/t09450035.png" />" ''J. Diff. Geom.'' , '''17''' (1982) pp. 503–521</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R. Kirby, "Stable homeomorphisms and the annulus conjecture" ''Ann. of Math.'' , '''89''' (1969) pp. 575–582</TD></TR><TR><TD valign="top">[a4a]</TD> <TD valign="top"> E.E. Moise, "Affine structures in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094500/t09450036.png" />-manifolds I" ''Ann. of Math.'' , '''54''' (1951) pp. 506–533</TD></TR><TR><TD valign="top">[a4b]</TD> <TD valign="top"> E.E. Moise, "Affine structures in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094500/t09450037.png" />-manifolds II, III" ''Ann. of Math.'' , '''55''' (1952) pp. 172–176; 203–222</TD></TR><TR><TD valign="top">[a4c]</TD> <TD valign="top"> E.E. Moise, "Affine structures in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094500/t09450038.png" />-manifolds IV" ''Ann. of Math.'' , '''56''' (1952) pp. 96–114</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> M. Brown, H. Gluck, "Stable structures on manifolds I-III" ''Ann. of Math.'' , '''79''' (1974) pp. 1–58</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> T. Radó, "Über den Begriff der Riemannsche Fläche" ''Acta Univ. Szeged'' , '''2''' (1924–1926) pp. 101–121</TD></TR></table> | ||
Latest revision as of 08:26, 6 June 2020
in topology
A topological image of the closed part of the plane comprised between two non-identical concentric circles. A two-dimensional annulus is an orientable two-dimensional manifold of genus zero with two boundary components.
Comments
Thus, a $ 2 $- dimensional annulus is homeomorphic to $ S ^ {1} \times I $, where $ S ^ {1} $ is the circle and $ I $ the interval. An $ n $- dimensional annulus is a space homeomorphic to $ S ^ {n-} 1 \times I $. The $ n $- dimensional annulus conjecture states that for any homeomorphism $ h: \mathbf R ^ {n} \rightarrow \mathbf R ^ {n} $ such that $ h( B ^ {n} ) \subset \mathop{\rm Int} ( B ^ {n} ) $, the interior of $ B ^ {n} $, the closed difference
$$ B ^ {n} \setminus h( \mathop{\rm Int} ( B ^ {n} )) $$
is homeomorphic to the annulus $ S ^ {n-} 1 \times I $. Here, $ B ^ {n} = \{ {x \in \mathbf R ^ {n} } : {\| x \| \leq 1 } \} $.
The stable homeomorphism conjecture asserts that any orientation-preserving homeomorphism $ h: \mathbf R ^ {n} \rightarrow \mathbf R ^ {n} $ can be written as a finite product, $ h = h _ {1} \dots h _ {m} $, where each $ h _ {i} $ is the identity on some open subset of $ \mathbf R ^ {n} $.
The stable homeomorphism conjecture for dimension $ n $ implies the annulus conjecture for dimension $ n $.
The stable homeomorphism conjecture (and hence the annulus conjecture) has finally been established for all $ n $: $ n= 1 $, classical; $ n= 2 $, [a6]; $ n= 3 $,
- $ n \geq 5 $,
[a3]; and, finally, $ n= 4 $, [a2], as an application of a special controlled $ h $- cobordism theorem in dimension $ 5 $, called the thin $ h $- cobordism theorem or Quinn's thin $ h $- cobordism theorem.
References
| [a1] | R.D. Edwards, "The solution of the 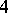 -dimensional annulus conjecture (after Frank Quinn)" Contemporary Math. , 35 (1984) pp. 211–264 -dimensional annulus conjecture (after Frank Quinn)" Contemporary Math. , 35 (1984) pp. 211–264 |
| [a2] | F. Quinn, "Ends of maps III: dimensions 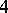 and and  " J. Diff. Geom. , 17 (1982) pp. 503–521 " J. Diff. Geom. , 17 (1982) pp. 503–521 |
| [a3] | R. Kirby, "Stable homeomorphisms and the annulus conjecture" Ann. of Math. , 89 (1969) pp. 575–582 |
| [a4a] | E.E. Moise, "Affine structures in  -manifolds I" Ann. of Math. , 54 (1951) pp. 506–533 -manifolds I" Ann. of Math. , 54 (1951) pp. 506–533 |
| [a4b] | E.E. Moise, "Affine structures in  -manifolds II, III" Ann. of Math. , 55 (1952) pp. 172–176; 203–222 -manifolds II, III" Ann. of Math. , 55 (1952) pp. 172–176; 203–222 |
| [a4c] | E.E. Moise, "Affine structures in  -manifolds IV" Ann. of Math. , 56 (1952) pp. 96–114 -manifolds IV" Ann. of Math. , 56 (1952) pp. 96–114 |
| [a5] | M. Brown, H. Gluck, "Stable structures on manifolds I-III" Ann. of Math. , 79 (1974) pp. 1–58 |
| [a6] | T. Radó, "Über den Begriff der Riemannsche Fläche" Acta Univ. Szeged , 2 (1924–1926) pp. 101–121 |
Two-dimensional annulus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Two-dimensional_annulus&oldid=17821