Thom space
A topological space associated with a vector (or sphere) bundle or spherical fibration.
Let  be a vector bundle over a CW-complex
be a vector bundle over a CW-complex  . Suppose that one is given a Riemannian metric on it, and consider the unit-disc bundle
. Suppose that one is given a Riemannian metric on it, and consider the unit-disc bundle  associated with
associated with  . In
. In  lies the unit-sphere subbundle
lies the unit-sphere subbundle  ; the quotient space
; the quotient space  is the Thom space of the bundle
is the Thom space of the bundle  , denoted by
, denoted by  . For a compact base space
. For a compact base space 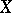 , the Thom space can also be described as the one-point compactification of the total space of the bundle
, the Thom space can also be described as the one-point compactification of the total space of the bundle  . Moreover, the Thom space is the cone of the projection
. Moreover, the Thom space is the cone of the projection 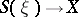 and in this way one can define the Thom space of any spherical fibration. Of course, the Thom space is also defined for any bundle with fibre
and in this way one can define the Thom space of any spherical fibration. Of course, the Thom space is also defined for any bundle with fibre 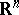 .
.
Let  be the group of orthogonal transformations of the space
be the group of orthogonal transformations of the space  . Over its classifying space
. Over its classifying space  there is the
there is the  -dimensional vector bundle
-dimensional vector bundle 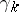 , associated with the universal
, associated with the universal  -bundle. The Thom space
-bundle. The Thom space  is often denoted by
is often denoted by 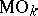 or
or  , and is called the Thom space of the group
, and is called the Thom space of the group  . Analogously one introduces the Thom spaces
. Analogously one introduces the Thom spaces  ,
, 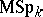 , etc., where
, etc., where 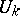 and
and 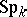 are the unitary and symplectic groups, respectively.
are the unitary and symplectic groups, respectively.
The role of the Thom space is to allow one to reduce a series of geometric problems to problems in homotopic topology, and hence to algebraic problems. Thus, the problem of computing a bordism group reduces to the problem of computing a homotopy group of a Thom space 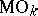 ,
,  , etc. (cf. [1], [2], and also Cobordism). The problem of classifying smooth manifolds reduces to the study of the homotopy properties of the Thom space of the normal bundle (cf. [3]). The problem of realizing cycles by submanifolds (cf. Steenrod problem) reduces to the study of the cohomology of the Thom spaces
, etc. (cf. [1], [2], and also Cobordism). The problem of classifying smooth manifolds reduces to the study of the homotopy properties of the Thom space of the normal bundle (cf. [3]). The problem of realizing cycles by submanifolds (cf. Steenrod problem) reduces to the study of the cohomology of the Thom spaces  and
and  , etc. (see also Transversal mapping; Tubular neighbourhood).
, etc. (see also Transversal mapping; Tubular neighbourhood).
The construction of Thom spaces is natural on the category of bundles: Any morphism of (vector) bundles  induces a continuous mapping
induces a continuous mapping  . In particular, the Thom space of an
. In particular, the Thom space of an  -dimensional bundle over a point is
-dimensional bundle over a point is  , and hence for any
, and hence for any  -dimensional bundle
-dimensional bundle 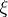 over
over  and any point
and any point  there is an inclusion
there is an inclusion  (induced by the inclusion of the fibre over
(induced by the inclusion of the fibre over  ). If
). If 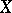 is path connected, then all such inclusions are homotopic, and one can talk about the mapping
is path connected, then all such inclusions are homotopic, and one can talk about the mapping 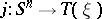 , which is unique up to homotopy.
, which is unique up to homotopy.
For vector bundles  and
and 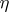 over
over  and
and 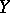 , respectively, one can define the bundle
, respectively, one can define the bundle 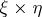 over
over 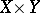 . Then
. Then  (cf. [4]). In particular, for the trivial bundle
(cf. [4]). In particular, for the trivial bundle  one has
one has  , where
, where  is the suspension operator, so that
is the suspension operator, so that  . This circumstance allows one to construct spectra of Thom spaces, cf. Thom spectrum.
. This circumstance allows one to construct spectra of Thom spaces, cf. Thom spectrum.
For a multiplicative generalized cohomology theory 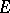 (cf. Generalized cohomology theories) there is a pairing
(cf. Generalized cohomology theories) there is a pairing
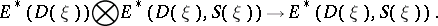 |
There arises a pairing
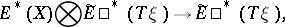 |
so that 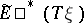 is an
is an  -module, and this is used in constructing the Thom isomorphism.
-module, and this is used in constructing the Thom isomorphism.
The following Atiyah duality theorem is important and often used (cf. [4], [5]): If  is a smooth manifold with boundary
is a smooth manifold with boundary  (possibly empty) and
(possibly empty) and  is its normal bundle, then the Thom space
is its normal bundle, then the Thom space 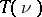 is in
is in 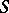 -duality with
-duality with  .
.
References
| [1] | R. Thom, "Quelques propriétés globales des variétés différentiables" Comm. Math. Helv. , 28 (1954) pp. 17–86 |
| [2] | R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) |
| [3] | W.B. Browder, "Surgery on simply-connected manifolds" , Springer (1972) |
| [4] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
| [5] | M. Atiyah, "Thom complexes" Proc. London Math. Soc. , 11 (1961) pp. 291–310 |
Comments
References
| [a1] | J. Dieudonné, "A history of algebraic and differential topology 1900–1960" , Birkhäuser (1989) |
Thom space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Thom_space&oldid=17782