Supersymmetry
The first appearance of supersymmetry is Grassmann's definition of an algebra that, although non-commutative, is commutative up to a sign factor. The Grassmann algebra (or exterior algebra) of a vector space is perhaps the earliest example of a class of algebras, supercommutative associative algebras, which appear extensively in topology (e.g. cohomology algebras, Steenrod algebras, and Hopf algebras (in the sense of [a13]), cf. also Steenrod algebra; Hopf algebra), and in geometry (e.g., the de Rham complex; cf. also de Rham cohomology). Lie superalgebras, the analogous generalization of Lie algebras (cf. also Superalgebra), first appeared in deformation theory, in a geometric context, in the work of A. Frölicher and A. Nijenhuis in the late 1950s, and, in an algebraic context, in the work of M. Gerstenhaber in the 1960s. In the early 1970s, Lie superalgebras and Lie supergroups arose in physics, where they were used to describe transformations (symmetries) connecting bosons, which are described by commuting variables, and fermions, which are described by anti-commuting variables. For more details, see [a5], [a3], [a6], [a16] and the original articles cited therein.
A $\mathbf{Z}_{2}$-graded vector space, or super vector space, is a vector space $V$ which is a direct sum of two components, $V = V _ { \bar{0}} \oplus V _ { \bar{1} }$. Vectors belonging to the summands are called homogeneous, and the parity function, defined by $p ( x ) = \overline{0}$ for $x \in V _ { \bar{0} }$ and $p ( x ) = \overline{1}$ for $x \in V _ { \overline{1} }$, distinguishes between those in $V _ { \overline{0} }$, called even vectors, and those in $V _ { \overline{1} }$, called odd vectors. In the super vector space representing physical particles, the even vectors represent bosons and the odd vectors represent fermions.
The term superalgebra is used for a super vector space with a bilinear product $x \otimes y \rightarrow x . y$ that preserves the grading, $p ( x . y ) = p ( x ) + p ( y )$. For example, a Lie superalgebra is a super vector space, $L = L _ { \overline{0} } \oplus L _ { \overline{1} }$, together with a bracket preserving the grading, and such that $[ x , . ]$ is a super derivation. In other words,
\begin{equation*} p ( [ x , y ] ) = p ( x ) + p ( y ), \end{equation*}
\begin{equation*} [ x , y ] = - ( - 1 ) ^ { p ( x ) p ( y ) } [ y , x ] , [ x , [ y , z ] ] = [ [ x , y ] , z ] + ( - 1 ) ^ { p ( x ) p ( y ) } [ y , [ x , z ] ]. \end{equation*}
Note that $L_{\overline{0}}$ is a Lie algebra in the standard sense.
The Lie superalgebra first used by physicists, the physical supersymmetry algebra, has an even component which is the standard Poincaré algebra $\operatorname{so}( 1,3 ) \oplus \mathbf{R} ^ { 1,3 }$ (cf. also Contraction of a Lie algebra). The odd component consists of spinors, which, when represented as symmetries of physical fields, transform fermions to bosons, and conversely, thus defining a "supersymmetry" . V.G. Kac [a9] has given a complete classification of the finite-dimensional simple Lie superalgebras over the complex numbers. There are two essentially different types: classical and Cartan superalgebras. The classical simple superalgebras, characterized by having an $L_{\overline{0}}$ which is reductive (cf. also Lie algebra, reductive), include the Wess–Zumino spin-conformal Lie superalgebra, which extends the physical supersymmetry algebra described above, see [a6]. The Cartan superalgebras have infinite-dimensional generalizations which play an important role in conformal field theory, see [a1] and references therein.
In categorical terms, super vector spaces form a symmetric monoidal Abelian category with monoidal structure defined by
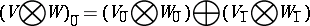 |
and
 |
and with symmetry defined by
\begin{equation*} B _ {{ V } \bigotimes { W }} ( x \bigotimes y ) = ( - 1 ) ^ { p ( x ) p ( y ) } ( y \bigotimes x ). \end{equation*}
The operator $B$ appears in any supersymmetric analogue of a classical formula which involves moving one element past another. The basic rule, sometimes called the supersymmetric "sign convention" , states that a factor of $( - 1 ) ^ { p ( x ) p ( y ) }$ appears whenever two elements, $x$, $y$ are flipped. (The sign convention does not always lead to a straightforward supersymmetric analogue, see the discussion of superdeterminants below.) The symmetric groups $\sum _ { n }$ act on the $n$th tensor power of a super vector space and there exist super analogues of the usual representation theory, e.g. Schur's double centralizer theorem, Young diagrams [a4].
If $A$ is an associative superalgebra with product $a \otimes b \rightarrow a b$, the supercommutator is defined by $[ a , b ] = a b - ( - 1 ) ^ { p ( a ) p ( b ) } b a$ for homogeneous elements, and extended linearly. Then $A$ is supercommutative if and only if the supercommutator is identically zero. In characteristic other than $2$, this implies that odd elements are nilpotent of order $2$. The symmetric algebra of a super vector space $V$ is defined as the quotient of the tensor $\mathcal{T} ( V )$ by the ideal $\mathcal{I} = \langle x \otimes y - B ( x \otimes y ) \rangle$. Since the algebra $\mathcal{T} ( V )$ inherits a $\mathbf{Z}_{2}$-grading, so does the quotient by the $\mathbf{Z}_{2}$ graded ideal, $\cal I$, and one has:
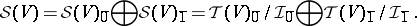 |
If $V$ is totally even, $V = V _ { \overline{0} }$, then ${\cal S} ( V )$ is the usual symmetric algebra. If $V$ is totally odd, $V = V _ { \overline{1} }$, then ${\cal S} ( V )$ is the Grassmann algebra (cf. also Cartan method of exterior forms), which is $\mathbf{Z}_{2}$-graded and supercommutative. Thus, the supersymmetric world unifies the standard concepts of commutativity and skew commutativity.
Another important example of an associative superalgebra is the universal enveloping algebra, $\mathcal{U} ( L )$, of a Lie superalgebra, $L$,
\begin{equation*} \mathcal{U} ( L ) = \mathcal{T} ( L ) / \left( x \bigotimes y - ( - 1 ) ^ { p ( x ) p ( y ) } y \bigotimes x - [ x , y ] \right). \end{equation*}
It is $\mathbf{Z}_{2}$-graded but not supercommutative. As in the standard case, it has an increasing filtration, with $k$th level ${\cal F} _ { k }$ equal to the subspace generated by $k$-fold products of elements of $L$. There is an analogue of the Poincaré–Birkhoff–Witt theorem (cf. Birkhoff–Witt theorem), stating that the associated graded algebra is isomorphic to $S ( L )$; see [a6].
A module over a superalgebra, $A$, is assumed to have a $\mathbf{Z}_{2}$-grading which is compatible with the $A$-action. As in the classical case, every left ($\mathbf{Z}_{2}$-graded) module $M$ over a supercommutative algebra $A$ becomes naturally an $A$-bimodule under the right action $m a = ( - 1 ) ^ { p ( m ) p ( a ) } a m$. The parity exchange functor is defined by $\Pi ( M ) _ { \overline{0}} = M _ { \overline{\text{l}} }$, $\Pi ( M ) _ { \overline{1} } = M _ { \overline{0} }$. The free finitely-generated $A$-module of rank $p | q$ is $A ^ { p | q } = A ^ { \oplus p } \oplus \Pi ( A ) ^ { \oplus q }$. Since the left and right module structures do not coincide, one has to distinguish between left and right $A$-module morphisms. After settling for a convention, say of considering the (symmetric monoidal) category of right $A$-modules, $\operatorname{Mod}_{A}$. Then, using right coordinates in $M = A ^ { p | q}$ and in $N = A ^ {r |s} $, the action of a morphism $t$ on an element $m \in M$ is given by left multiplication of the corresponding matrix, $T$, with the column vector of right coordinates of $m$. The matrix,
\begin{equation*} T = \left( \begin{array} { c c } { P } & { Q } \\ { R } & { S } \end{array} \right) \end{equation*}
is even (odd) if the submatrices $P$, $S$ have even (odd) coefficients and the submatrices $Q$, $R$ have odd (even) coefficients, respectively. In defining the dual module, one must distinguish again between left and right $A$-module morphisms into $A$. Having fixed one choice of dual, say dual on the left, then, as usual, given a morphism $t : M \rightarrow N$ there is dual morphism $t ^ { * } : N ^ { * } \rightarrow M ^ { * }$ with the property
\begin{equation*} \langle t ^ { * } ( n ^ { * } ) , m \rangle = ( - 1 ) ^ { p ( t ) p ( n ^ { * } ) } \langle n ^ { * } , t ( m ) \rangle. \end{equation*}
In terms of matrices, this leads to the definition a supertranspose, $T ^ { \operatorname {st} }$. However, in contrast to the usual transpose, the supertranspose is not an involution but has order $4$, see [a15].
The supertrace is defined on $\operatorname{Mat} (p | q )$ (square matrices acting on $A ^ { p | q} $) by $\operatorname { str } ( T ) = \operatorname { tr } P - ( - 1 ) ^ { p ( S ) } \operatorname { tr } S$, and has the same properties as the usual trace (cf. also Trace of a square matrix). It is a morphism of $A$-modules, vanishes on supercommutators, and is invariant under the supertranspose. The fundamental difference is that $\operatorname { str } ( \operatorname { id} ) = p - q$.
A definition of superdeterminant is more complicated. In the standard case the determinant of an $( n \times n )$-matrix $T$ can be defined using the induced action on the $n$th exterior power $\wedge ^ { n } V$ of the vector space $V$ on which $T$ operates. Since $\operatorname { dim } ( \wedge ^ { n } V ) = 1$, the induced action is multiplication by a scalar, $\operatorname { det } ( T )$. When $V$ is $\mathbf{Z}_{2}$-graded and $\operatorname { lim } ( V _ { \overline{1} } ) \neq 0$, there is no longer a top exterior power of dimension $1$ and the standard approach will not work. F.A. Berezin has given a definition of a superdeterminant (now called the Berezinian) for invertible even endomorphisms $T \in \mathcal{L} ( p | q )$,
\begin{equation*} \operatorname { Ber } ( T ) = \operatorname { det } ( P - Q S ^ { - 1 } R ) \operatorname { det } ( S ) ^ { - 1 }. \end{equation*}
It has the important, and not obvious, property of being a multiplicative homomorphism. Also, $\operatorname { Ber } ( T ^ { \text{st} } ) = \operatorname { Ber } ( T )$. It is possible to define the Berezinian in the spirit of the classical definition using the Koszul complex, see [a15]. Other possible definitions have been studied by I. Kantor, [a10].
Supergeometry begins with the definition of a real (complex) superdomain of dimension $( p , q )$, which is a triple ${\cal U} = ( U , {\cal O ( U )} , \text { ev } )$ consisting of an open set $U \subset \mathbf{R} ^ { p }$ (or $U \subset \mathbf{C} ^ { p }$), a supercommutative superalgebra of functions $\mathcal{O} ( U ) = \mathcal{O} ( U ) \otimes \Lambda ( \xi _ { 1 } , \ldots , \xi _ { q } )$, where $\mathcal{O} ( U )$ is the appropriate algebra of functions (smooth, analytic, etc.), and an evaluation mapping $\operatorname { ev } _ { x } ( a )$ defined for pairs $x \in U$ and $a \in \cal O ( U )$, $\operatorname { ev } _ { x } ( f \otimes 1 ) = f ( x )$ and $\operatorname { ev } _ { x } ( 1 \otimes \xi _ { i } ) = 0$. A mapping of superdomains $\varphi : \mathcal{U} \rightarrow \mathcal{V}$ is a pair $\varphi = ( \varphi _ { 0 } , \varphi ^ { * } )$, where $\varphi _ { 0 } : U \rightarrow V$, is a mapping of topological spaces, $\varphi ^ { * } : \mathcal{O} ( \mathcal{V} ) \rightarrow \mathcal{O} ( \mathcal{U} )$ is a mapping of superalgebras and $\operatorname { ev } _ { x } ( \varphi ^ { * } ( a ) ) = \operatorname { ev } _ { \varphi _ { 0 } ( x ) } ( a )$. A super-manifold (cf., also Super-manifold) is a pair $( M , \mathcal{O} _ { M } )$ consisting of a manifold $M$ and a sheaf of supercommutative algebras, $\mathcal{O} _ { M }$, which is locally isomorphic to a superdomain. Starting with these basic definitions one can develop a theory of super-manifolds analogous to the classical theory, see [a2], [a11], [a12], [a15]. Supersymmetric Yang–Mills theory [a15], [a18] and the theory of superstrings [a8] (which may be the key to a unified theory of the fundamental forces of nature) have stimulated an explosion of new ideas in mathematics, in particular in the study of invariants of $4$-manifolds, see [a2], [a17].
The theory of quantum groups has led to an extended concept of symmetry for modules over a quasi-triangular Hopf algebra, $A$, with $R$-matrix, $R = \sum a _ { i } \otimes b _ { i }$ and braiding $B_{M\otimes N}(m\otimes n)= \sum b_i n \otimes a_i m $. In the triangular case, $R R ^ { 21 } = 1 \otimes 1$, where $R ^ { 21 } = \sum b _ { i } \otimes a _ { i }$, the braiding is a symmetry and there is a theory of quantum commutativity [a7]. For general Hopf algebras $H$ (cf. also Hopf algebra), there is a theory of "H-commutativity" , related to Yetter–Drinfel'd categories, [a14], [a19].
References
| [a1] | V.G. Kac, "Classification of infinite-dimensional simple linearly compact Lie superalgebras" Adv. Math. , 139 (1998) pp. 1–55 |
| [a2] | J. Bernstein, "Lectures on supersymmetry" P. Deligne (ed.) P. Etingof (ed.) D. Freed (ed.) L. Jeffrey (ed.) D. Kazhdan (ed.) D. Morrison (ed.) E. Witten (ed.) , Quantum Fields and Strings: A Course for Mathematicians , Amer. Math. Soc. (to appear) |
| [a3] | F.A. Berezin, G.I. Kats, "Lie groups with noncommuting parameters" Mat. Sb. USSR , 11 (1970) pp. 311–320 |
| [a4] | A. Berele, A. Regev, "Hook Young diagrams with applications to combinatorics and to representations of Lie superalgebras" Adv. Math. , 64 : 2 (1987) pp. 118–175 |
| [a5] | F.A. Berezin, "The mathematical basis of supersymmetric field theories" Soviet J. Nucl. Phys. , 29 (1979) pp. 857–866 |
| [a6] | L. Corwin, Y. Ne'eman, S. Sternberg, "Graded Lie algebras in mathematics and physics" Rev. Mod. Phys. , 47 (1975) pp. 573–604 |
| [a7] | M. Cohen, S. Westreich, "From supersymmetry to quantum commutativity" J. Algebra , 168 (1994) pp. 1–27 |
| [a8] | M.B. Green, J.H. Schwarz, E. Witten, "Superstring Theory" , Mon. Math. Phys. , Cambridge Univ. Press (1987) |
| [a9] | V.G. Kac, "Lie superalgebras" Adv. Math. , 26 (1977) pp. 8–96 |
| [a10] | I. Kantor, "On the concept of determinant in the supercase" Commun. Algebra , 22 : 10 (1994) pp. 3679–3739 |
| [a11] | B. Kostant, "Graded manifolds, graded Lie theory and prequantization" , Differential Geom. Methods in Math. Phys. Proc. Symp. Bonn 1975 , Lecture Notes Math. , 570 , Springer (1977) pp. 177–306 |
| [a12] | D.A. Leites, "Introduction to the theory of supermanifolds" Russian Math. Surveys , 35 (1980) pp. 3–57 |
| [a13] | J. Milnor, J. Moore, "On the Structure of Hopf algebras" Ann. of Math. , 81 (1965) pp. 211–264 |
| [a14] | S. Majid, "Foundations of quantum group theory" , Cambridge Univ. Press (1995) |
| [a15] | Yu.I. Manin, "Gauge field theory and complex geometry" , Springer (1984) |
| [a16] | V.I. Ogievetski, L. Mezinchesku, "Boson-fermion symmetries and superfields" Soviet Phys. Uspekhi , 18 : 12 (1975) pp. 960–981 |
| [a17] | N. Seiberg, E. Witten, "Monopoles, duality, and chiral symmetry breaking in $N = 2$ supersymmetric QCD" Nucl. Phys. B , 431 (1994) pp. 581–640 |
| [a18] | S. Shnider, R.O. Wells Jr., "Supermanifolds, Super Twistor Spaces and Super Yang–Mills Fields" , Sém. Math. Sup. , Les Presses de l'Univ. Montréal (1989) |
| [a19] | D. Yetter, "Quantum groups and representations of monoidal categories" Math. Proc. Cambridge Philos. Soc. , 108 (1990) pp. 261–290 |
Supersymmetry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Supersymmetry&oldid=50836