Contraction of a Lie algebra
An operation inverse to deformation of a Lie algebra. Let 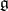 be a finite-dimensional real Lie algebra, let
be a finite-dimensional real Lie algebra, let 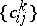 be its set of structure constants with respect to a fixed basis
be its set of structure constants with respect to a fixed basis  and let
and let 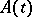 ,
, 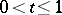 , be a curve in the group of non-singular linear transformations of
, be a curve in the group of non-singular linear transformations of 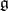 such that
such that 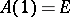 . Let
. Let 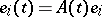 and let
and let  be the structure constants of
be the structure constants of 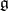 with respect to the basis
with respect to the basis 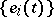 . If
. If 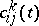 tends to some limit
tends to some limit 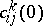 as
as 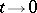 , then the algebra
, then the algebra  defined by these constants relative to the original basis is called a contraction of the initial algebra
defined by these constants relative to the original basis is called a contraction of the initial algebra 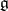 . The contraction
. The contraction 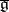 is also a Lie algebra, moreover
is also a Lie algebra, moreover 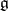 can be obtained by means of a deformation of
can be obtained by means of a deformation of 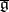 . If
. If 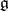 is the Lie algebra of a Lie group
is the Lie algebra of a Lie group 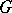 , then the Lie group
, then the Lie group 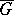 corresponding to
corresponding to 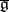 is called a contraction of the group
is called a contraction of the group 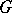 .
.
Although 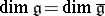 , in general these algebras are not isomorphic. For example, if
, in general these algebras are not isomorphic. For example, if 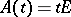 , then
, then 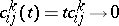 , so for this contraction the limit algebra is always commutative. The natural generalization of this example is the following: Let
, so for this contraction the limit algebra is always commutative. The natural generalization of this example is the following: Let  be a subalgebra in
be a subalgebra in 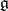 , let
, let  be a subspace complementary to
be a subspace complementary to  , let, moreover,
, let, moreover, 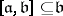 and
and 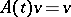 for each
for each 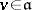 ,
,  for
for 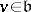 . Then in the limit
. Then in the limit 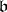 becomes a commutative ideal of
becomes a commutative ideal of 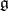 , while at the same time multiplication in
, while at the same time multiplication in  and the operation of
and the operation of  on
on 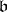 remain the same.
remain the same.
In particular, let 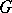 be the Lorentz group,
be the Lorentz group, 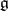 its Lie algebra and
its Lie algebra and  the subalgebra corresponding to the subgroup of rotations of
the subalgebra corresponding to the subgroup of rotations of  -dimensional space. Then the described contraction of
-dimensional space. Then the described contraction of  gives the Lie algebra of the Galilean group
gives the Lie algebra of the Galilean group 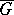 (see Galilean transformation; Lorentz transformation). Hence the Lorentz algebra is a deformation of the Galilean algebra, and it can be shown that the complexification of the Galilean algebra has no other deformations; in the real case the Galilean algebra can also be a contraction of the orthogonal Lie algebra
(see Galilean transformation; Lorentz transformation). Hence the Lorentz algebra is a deformation of the Galilean algebra, and it can be shown that the complexification of the Galilean algebra has no other deformations; in the real case the Galilean algebra can also be a contraction of the orthogonal Lie algebra 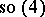 . An equivalent method of obtaining the Galilean algebra from the Lorentz algebra is to define the Lorentz algebra as the algebra preserving the Minkowski form
. An equivalent method of obtaining the Galilean algebra from the Lorentz algebra is to define the Lorentz algebra as the algebra preserving the Minkowski form  , and then letting the velocity of light tend to
, and then letting the velocity of light tend to 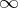 . As long as
. As long as 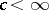 , the algebra arising is isomorphic to
, the algebra arising is isomorphic to 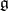 . Analogously, deforming the Poincaré algebra (the inhomogeneous Lorentz algebra), it is possible to obtain the de Sitter algebras
. Analogously, deforming the Poincaré algebra (the inhomogeneous Lorentz algebra), it is possible to obtain the de Sitter algebras 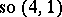 and
and 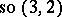 of motions of a space of constant curvature. Correspondingly, setting the curvature to 0, one obtains the Poincaré group as a contraction of the de Sitter group.
of motions of a space of constant curvature. Correspondingly, setting the curvature to 0, one obtains the Poincaré group as a contraction of the de Sitter group.
The connection between these algebras can be extended to representations. If, as in the described examples, there is a matrix 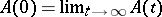 , then each representation
, then each representation 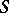 of
of  generates a representation
generates a representation 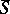 of the contraction algebra by the formula
of the contraction algebra by the formula
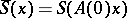 |
for any 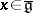 . The inverse operation (deformation of a representation) is not possible, in general.
. The inverse operation (deformation of a representation) is not possible, in general.
References
| [1] | A.O. Barut, R. Raçzka, "Theory of group representations and applications" , 1–2 , PWN (1977) |
| [2] | E. Inönü, E.P. Wigner, "On the contraction of groups and their representations" Proc. Nat. Acad. Sci. USA , 39 (1953) pp. 510–524 |
| [3] | E.J. Saletan, "Contraction of Lie groups" J. Math. Phys. , 2 (1961) pp. 1–22; 742 |
Contraction of a Lie algebra. A.K. Tolpygo (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contraction_of_a_Lie_algebra&oldid=12965