Difference between revisions of "Statistical game"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | A [[Two-person zero-sum game|two-person zero-sum game]] in which player | + | <!-- |
| + | s0873901.png | ||
| + | $#A+1 = 10 n = 2 | ||
| + | $#C+1 = 10 : ~/encyclopedia/old_files/data/S087/S.0807390 Statistical game | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | A [[Two-person zero-sum game|two-person zero-sum game]] in which player $ I $ | ||
| + | is interpreted as nature, player $ II $ | ||
| + | as a statistician, player $ I $' | ||
| + | s strategy is a random process, player $ II $' | ||
| + | s strategy is a decision rule (decision function), and the pay-off function of player $ I $ | ||
| + | is the loss function ( "risk" ) of the statistician. Player $ I $' | ||
| + | s mixed strategy will then be a probability measure on the set of random processes, player $ II $' | ||
| + | s mixed strategy will be a randomized decision rule, and player $ I $' | ||
| + | s pay-off function is defined as the mathematical expectation of the statistician's loss function. Statistical games arose out of problems of [[Mathematical statistics|mathematical statistics]] (for example, the problems of estimating parameters, testing hypotheses, etc.), in which the minimax test is used (see [[Minimax principle|Minimax principle]]). A systematic description of problems of mathematical statistics (including problems of sequential analysis) as statistical games was first introduced by A. Wald, who proved the validity of the minimax theorem for a broad class of statistical games (see [[#References|[1]]]). This theorem provides a method for solving problems of mathematical statistics, since in a number of cases it is easier and more convenient to find the maximin than the minimax, which, in turn, makes it easier to find an optimal randomized rule. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Wald, "Statistical decision functions" , Wiley (1950)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D. Blackwell, M.A. Girshick, "Theory of games and statistical decisions" , Dover, reprint (1979)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Wald, "Statistical decision functions" , Wiley (1950)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D. Blackwell, M.A. Girshick, "Theory of games and statistical decisions" , Dover, reprint (1979)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Statistical games are considered when one deals with worst case designs. A modern version of statistical games lies at the heart of | + | Statistical games are considered when one deals with worst case designs. A modern version of statistical games lies at the heart of $ H ^ \infty $ |
| + | control (a subject within automatic control, cf. also [[H^infinity-control-theory| $ H ^ \infty $ | ||
| + | control theory]]), see [[#References|[a1]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Doyle, K. Glover, P. Khargonekar, B. Francis, "State-space solutions to standard <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087390/s08739011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087390/s08739012.png" /> control problems" ''IEEE Trans. Autom. Control'' , '''AC34''' : 8 (1989) pp. 831–847</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.L. Savage, "The foundation of statistics" , Wiley (1954)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.W. Milnor, "Games against nature" R.M. Thrall (ed.) C.H. Coombs (ed.) R.L. Davis (ed.) , ''Decision processes'' , Wiley (1954) pp. 49–59</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Doyle, K. Glover, P. Khargonekar, B. Francis, "State-space solutions to standard <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087390/s08739011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087390/s08739012.png" /> control problems" ''IEEE Trans. Autom. Control'' , '''AC34''' : 8 (1989) pp. 831–847</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.L. Savage, "The foundation of statistics" , Wiley (1954)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.W. Milnor, "Games against nature" R.M. Thrall (ed.) C.H. Coombs (ed.) R.L. Davis (ed.) , ''Decision processes'' , Wiley (1954) pp. 49–59</TD></TR></table> | ||
Latest revision as of 08:23, 6 June 2020
A two-person zero-sum game in which player $ I $
is interpreted as nature, player $ II $
as a statistician, player $ I $'
s strategy is a random process, player $ II $'
s strategy is a decision rule (decision function), and the pay-off function of player $ I $
is the loss function ( "risk" ) of the statistician. Player $ I $'
s mixed strategy will then be a probability measure on the set of random processes, player $ II $'
s mixed strategy will be a randomized decision rule, and player $ I $'
s pay-off function is defined as the mathematical expectation of the statistician's loss function. Statistical games arose out of problems of mathematical statistics (for example, the problems of estimating parameters, testing hypotheses, etc.), in which the minimax test is used (see Minimax principle). A systematic description of problems of mathematical statistics (including problems of sequential analysis) as statistical games was first introduced by A. Wald, who proved the validity of the minimax theorem for a broad class of statistical games (see [1]). This theorem provides a method for solving problems of mathematical statistics, since in a number of cases it is easier and more convenient to find the maximin than the minimax, which, in turn, makes it easier to find an optimal randomized rule.
References
| [1] | A. Wald, "Statistical decision functions" , Wiley (1950) |
| [2] | D. Blackwell, M.A. Girshick, "Theory of games and statistical decisions" , Dover, reprint (1979) |
Comments
Statistical games are considered when one deals with worst case designs. A modern version of statistical games lies at the heart of $ H ^ \infty $ control (a subject within automatic control, cf. also $ H ^ \infty $ control theory), see [a1].
References
| [a1] | J. Doyle, K. Glover, P. Khargonekar, B. Francis, "State-space solutions to standard  and and 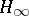 control problems" IEEE Trans. Autom. Control , AC34 : 8 (1989) pp. 831–847 control problems" IEEE Trans. Autom. Control , AC34 : 8 (1989) pp. 831–847 |
| [a2] | J.L. Savage, "The foundation of statistics" , Wiley (1954) |
| [a3] | J.W. Milnor, "Games against nature" R.M. Thrall (ed.) C.H. Coombs (ed.) R.L. Davis (ed.) , Decision processes , Wiley (1954) pp. 49–59 |
Statistical game. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Statistical_game&oldid=48813