Riemann sphere
A sphere in the Euclidean space $ \mathbf R ^ {3} ( \xi , \eta , t) $
onto which the extended complex plane $ \overline{\mathbf C}\; $
is conformally and one-to-one transformed under stereographic projection. For example, the unit sphere
$$ S _ {2} = \{ {( \xi , \eta , t) \in \mathbf R ^ {3} } : { \xi ^ {2} + \eta ^ {2} + t ^ {2} = 1 } \} $$
can be taken as the Riemann sphere and the plane $ \overline{\mathbf C}\; $ can be identified with the plane $ t = 0 $ such that the real axis coincides with the axis $ \eta = 0, t = 0 $ and the imaginary axis with the axis $ \xi = 0, t = 0 $ (see Fig.).
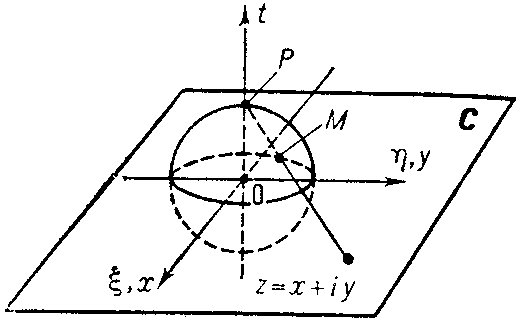
Figure: r082010a
Under stereographic projection to each point $ z = x + iy \neq \infty $ there corresponds the point $ M( \xi , \eta , t) \neq P( 0, 0, 1) $ obtained as the point of intersection of the ray drawn from the north pole of the sphere, $ P( 0, 0, 1) $, to the point $ z $ with the sphere $ S _ {2} $; the north pole $ P( 0, 0, 1) $ corresponds to the point at infinity, $ z = \infty $. Analytically this relation can be expressed by the formulas
$$ \tag{* } \xi + i \eta = \ \frac{2z}{| z | ^ {2} + 1 } ,\ \ t = \frac{| z | ^ {2} - 1 }{| z | ^ {2} + 1 } ,\ \ z = \frac{\xi + i \eta }{1-t }. $$
In other words, the correspondence (*) determines a differentiable imbedding of the one-dimensional complex projective space $ \mathbf C P ^ {1} $ into the space $ \mathbf R ^ {3} $ in the form of the sphere $ S _ {2} $. In many questions of the theory of functions, the extended complex plane is identified with the Riemann sphere. The exclusive role of the point at infinity of the plane $ \overline{\mathbf C}\; $ may be dispensed with if the distance between two points $ z, w \in \overline{\mathbf C}\; $ is taken to be the chordal, or spherical, distance $ \chi ( z, w) $ between their images $ M, N \in S _ {2} $:
$$ \chi ( z, w) = \frac{2| z- w | }{\sqrt {| z | ^ {2} + 1 } \sqrt {| w | ^ {2} + 1 } } , $$
$$ \chi ( z, \infty ) = \frac{2}{\sqrt {| z | ^ {2} + 1 } } . $$
A higher-dimensional complex projective space $ \mathbf C P ^ {n} $, $ n > 1 $, can be imbedded into the space $ \mathbf R ^ {n(n+ 2)} $ by a complex $ n $-dimensional stereographic projection, generalizing the formulas (*) (see [2]).
References
| [1] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
| [2] | B.A. Fuks, "Introduction to the theory of analytic functions of several complex variables" , Amer. Math. Soc. (1965) (Translated from Russian) |
| [a1] | L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. Chapt. 8 |
Riemann sphere. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_sphere&oldid=52811