Difference between revisions of "Riemann sphere"
(Importing text file) |
m (one references section) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | r0820101.png | ||
| + | $#A+1 = 28 n = 0 | ||
| + | $#C+1 = 28 : ~/encyclopedia/old_files/data/R082/R.0802010 Riemann sphere | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | can be taken as the Riemann sphere and the plane | + | A sphere in the Euclidean space $ \mathbf R ^ {3} ( \xi , \eta , t) $ |
| + | onto which the extended complex plane $ \overline{\mathbf C}\; $ | ||
| + | is conformally and one-to-one transformed under [[Stereographic projection|stereographic projection]]. For example, the unit sphere | ||
| + | |||
| + | $$ | ||
| + | S _ {2} = \{ {( \xi , \eta , t) \in \mathbf R ^ {3} } : { | ||
| + | \xi ^ {2} + \eta ^ {2} + t ^ {2} = 1 } \} | ||
| + | $$ | ||
| + | |||
| + | can be taken as the Riemann sphere and the plane $ \overline{\mathbf C}\; $ | ||
| + | can be identified with the plane $ t = 0 $ | ||
| + | such that the real axis coincides with the axis $ \eta = 0, t = 0 $ | ||
| + | and the imaginary axis with the axis $ \xi = 0, t = 0 $ (see Fig.). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082010a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r082010a.gif" /> | ||
| Line 9: | Line 29: | ||
Figure: r082010a | Figure: r082010a | ||
| − | Under stereographic projection to each point | + | Under stereographic projection to each point $ z = x + iy \neq \infty $ |
| − | + | there corresponds the point $ M( \xi , \eta , t) \neq P( 0, 0, 1) $ | |
| − | + | obtained as the point of intersection of the ray drawn from the north pole of the sphere, $ P( 0, 0, 1) $, | |
| − | + | to the point $ z $ | |
| − | + | with the sphere $ S _ {2} $; | |
| + | the north pole $ P( 0, 0, 1) $ | ||
| + | corresponds to the point at infinity, $ z = \infty $. | ||
| + | Analytically this relation can be expressed by the formulas | ||
| − | + | $$ \tag{* } | |
| + | \xi + i \eta = \ | ||
| − | + | \frac{2z}{| z | ^ {2} + 1 } | |
| + | ,\ \ | ||
| + | t = | ||
| + | \frac{| z | ^ {2} - 1 }{| z | ^ {2} + 1 } | ||
| + | ,\ \ | ||
| + | z = | ||
| + | \frac{\xi + i \eta }{1-t }. | ||
| + | $$ | ||
| − | + | In other words, the correspondence (*) determines a differentiable imbedding of the one-dimensional complex projective space $ \mathbf C P ^ {1} $ | |
| − | + | into the space $ \mathbf R ^ {3} $ | |
| − | + | in the form of the sphere $ S _ {2} $. | |
| − | + | In many questions of the theory of functions, the extended complex plane is identified with the Riemann sphere. The exclusive role of the point at infinity of the plane $ \overline{\mathbf C}\; $ | |
| + | may be dispensed with if the distance between two points $ z, w \in \overline{\mathbf C}\; $ | ||
| + | is taken to be the chordal, or spherical, distance $ \chi ( z, w) $ | ||
| + | between their images $ M, N \in S _ {2} $: | ||
| + | $$ | ||
| + | \chi ( z, w) = | ||
| + | \frac{2| z- w | }{\sqrt {| z | ^ {2} + 1 } \sqrt {| w | ^ {2} + 1 } } | ||
| + | , | ||
| + | $$ | ||
| − | = | + | $$ |
| + | \chi ( z, \infty ) = | ||
| + | \frac{2}{\sqrt {| z | ^ {2} + 1 } } | ||
| + | . | ||
| + | $$ | ||
| + | A higher-dimensional complex projective space $ \mathbf C P ^ {n} $, | ||
| + | $ n > 1 $, | ||
| + | can be imbedded into the space $ \mathbf R ^ {n(n+ 2)} $ | ||
| + | by a complex $ n $-dimensional stereographic projection, generalizing the formulas (*) (see [[#References|[2]]]). | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. Chapt. 8</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''1–2''' , Moscow (1976) (In Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> B.A. Fuks, "Introduction to the theory of analytic functions of several complex variables" , Amer. Math. Soc. (1965) (Translated from Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. Chapt. 8</TD></TR> | ||
| + | </table> | ||
Latest revision as of 13:59, 17 March 2023
A sphere in the Euclidean space $ \mathbf R ^ {3} ( \xi , \eta , t) $
onto which the extended complex plane $ \overline{\mathbf C}\; $
is conformally and one-to-one transformed under stereographic projection. For example, the unit sphere
$$ S _ {2} = \{ {( \xi , \eta , t) \in \mathbf R ^ {3} } : { \xi ^ {2} + \eta ^ {2} + t ^ {2} = 1 } \} $$
can be taken as the Riemann sphere and the plane $ \overline{\mathbf C}\; $ can be identified with the plane $ t = 0 $ such that the real axis coincides with the axis $ \eta = 0, t = 0 $ and the imaginary axis with the axis $ \xi = 0, t = 0 $ (see Fig.).
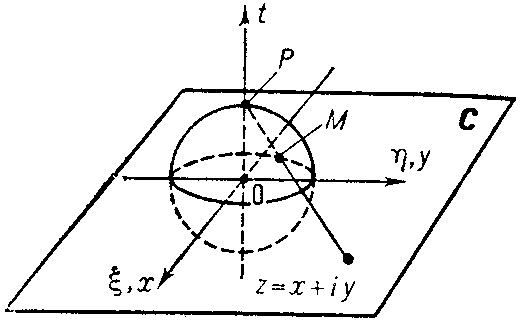
Figure: r082010a
Under stereographic projection to each point $ z = x + iy \neq \infty $ there corresponds the point $ M( \xi , \eta , t) \neq P( 0, 0, 1) $ obtained as the point of intersection of the ray drawn from the north pole of the sphere, $ P( 0, 0, 1) $, to the point $ z $ with the sphere $ S _ {2} $; the north pole $ P( 0, 0, 1) $ corresponds to the point at infinity, $ z = \infty $. Analytically this relation can be expressed by the formulas
$$ \tag{* } \xi + i \eta = \ \frac{2z}{| z | ^ {2} + 1 } ,\ \ t = \frac{| z | ^ {2} - 1 }{| z | ^ {2} + 1 } ,\ \ z = \frac{\xi + i \eta }{1-t }. $$
In other words, the correspondence (*) determines a differentiable imbedding of the one-dimensional complex projective space $ \mathbf C P ^ {1} $ into the space $ \mathbf R ^ {3} $ in the form of the sphere $ S _ {2} $. In many questions of the theory of functions, the extended complex plane is identified with the Riemann sphere. The exclusive role of the point at infinity of the plane $ \overline{\mathbf C}\; $ may be dispensed with if the distance between two points $ z, w \in \overline{\mathbf C}\; $ is taken to be the chordal, or spherical, distance $ \chi ( z, w) $ between their images $ M, N \in S _ {2} $:
$$ \chi ( z, w) = \frac{2| z- w | }{\sqrt {| z | ^ {2} + 1 } \sqrt {| w | ^ {2} + 1 } } , $$
$$ \chi ( z, \infty ) = \frac{2}{\sqrt {| z | ^ {2} + 1 } } . $$
A higher-dimensional complex projective space $ \mathbf C P ^ {n} $, $ n > 1 $, can be imbedded into the space $ \mathbf R ^ {n(n+ 2)} $ by a complex $ n $-dimensional stereographic projection, generalizing the formulas (*) (see [2]).
References
| [1] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
| [2] | B.A. Fuks, "Introduction to the theory of analytic functions of several complex variables" , Amer. Math. Soc. (1965) (Translated from Russian) |
| [a1] | L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. Chapt. 8 |
Riemann sphere. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_sphere&oldid=18286