Representation of a topological group
A mapping of the group 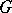 into the group of homeomorphisms of a topological space. Most often such a representation of
into the group of homeomorphisms of a topological space. Most often such a representation of  is understood to be a linear representation, moreover, a linear representation
is understood to be a linear representation, moreover, a linear representation 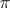 of
of 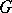 into a topological vector space
into a topological vector space 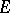 such that the vector function
such that the vector function 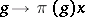 ,
, 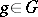 , defines for any
, defines for any 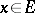 a continuous mapping of
a continuous mapping of 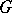 into
into 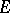 . In particular, every continuous representation of the group
. In particular, every continuous representation of the group 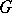 is a representation of the topological group
is a representation of the topological group  .
.
The theory of representations of topological groups is strongly connected with the representation theory of various topological group algebras (cf. Group algebra). The most important among these is the symmetric Banach measure algebra 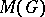 of the group
of the group 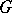 (the algebra of all regular Borel measures on
(the algebra of all regular Borel measures on 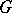 with finite total variation, in which multiplication is defined as convolution). Often one also uses the topological algebra
with finite total variation, in which multiplication is defined as convolution). Often one also uses the topological algebra 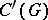 of all regular Borel measures on
of all regular Borel measures on 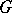 with finite total variation and with compact support. Multiplication in
with finite total variation and with compact support. Multiplication in 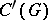 is defined as convolution, and the involution
is defined as convolution, and the involution 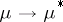 ,
, 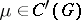 , is defined by
, is defined by
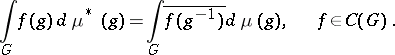 |
The topology of 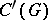 is compatible with the duality between this algebra and the algebra
is compatible with the duality between this algebra and the algebra 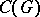 (of all continuous functions on
(of all continuous functions on 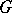 ), equipped with the compact-open topology. Various subalgebras of
), equipped with the compact-open topology. Various subalgebras of 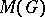 and
and 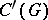 also play an important role. In particular, if
also play an important role. In particular, if 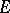 is a quasi-complete barrelled or complete locally convex space and
is a quasi-complete barrelled or complete locally convex space and 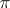 is a continuous representation of the topological group
is a continuous representation of the topological group 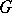 into
into 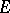 , then the formula
, then the formula
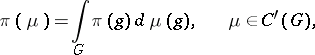 |
defines a weakly-continuous linear operator  on
on  , and the correspondence
, and the correspondence  is a representation of the algebra
is a representation of the algebra 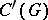 in
in 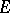 , uniquely defining the representation
, uniquely defining the representation 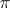 of the topological group. Here, a representation of a topological group, a (topologically) irreducible representation, an operator-irreducible representation, a totally irreducible representation, is equivalent to another representation of the topological group, etc., if and only if the corresponding representations of the algebra
of the topological group. Here, a representation of a topological group, a (topologically) irreducible representation, an operator-irreducible representation, a totally irreducible representation, is equivalent to another representation of the topological group, etc., if and only if the corresponding representations of the algebra 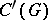 have the corresponding property.
have the corresponding property.
Let 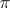 be a representation of a topological group
be a representation of a topological group 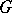 in a locally convex vector space
in a locally convex vector space 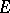 and let
and let  be the space dual to
be the space dual to 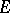 . Functions on
. Functions on 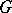 of the form
of the form 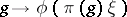 ,
, 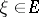 ,
, 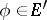 , are called matrix elements of
, are called matrix elements of 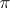 . If
. If 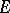 is a Hilbert space and
is a Hilbert space and 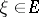 ,
, 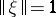 , then functions of the form
, then functions of the form 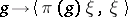 ,
, 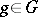 , are called spherical functions, corresponding to
, are called spherical functions, corresponding to 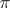 .
.
Suppose that 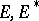 are dual locally convex spaces and let
are dual locally convex spaces and let 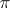 be a representation of a topological group
be a representation of a topological group 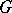 in
in 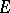 . The formula
. The formula 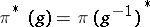 defines a representation
defines a representation 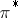 of
of 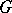 in
in 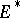 , called the adjoint, or contragredient, representation to
, called the adjoint, or contragredient, representation to 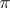 . Suppose that
. Suppose that 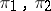 are representations of
are representations of 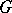 in locally convex spaces
in locally convex spaces  , respectively, let
, respectively, let 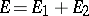 be the direct sum and let
be the direct sum and let 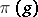 ,
, 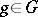 , be the continuous linear operator into
, be the continuous linear operator into 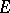 defined by
defined by
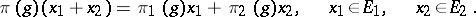 |
The mapping 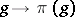 is a representation of
is a representation of 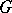 in
in 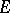 , called the direct sum of the representations
, called the direct sum of the representations 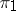 and
and 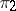 . In certain situations (in particular for unitary representations) one can define the tensor product of representations of a topological group and the direct sum of an infinite family of such representations. By restricting or extending the field of scalars, one introduces the operations of "realification" or complexification of representations.
. In certain situations (in particular for unitary representations) one can define the tensor product of representations of a topological group and the direct sum of an infinite family of such representations. By restricting or extending the field of scalars, one introduces the operations of "realification" or complexification of representations.
A representation of a topological group is called completely reducible if every closed invariant subspace has a complementary closed invariant subspace. A representation 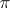 of a topological group
of a topological group 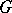 in a locally convex space
in a locally convex space 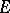 is called split (decomposable) if there exist closed invariant subspaces
is called split (decomposable) if there exist closed invariant subspaces 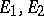 in
in 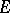 such that
such that 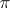 is equivalent to the direct sum of the subrepresentations
is equivalent to the direct sum of the subrepresentations 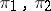 of
of 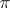 corresponding to the subspaces
corresponding to the subspaces 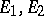 , respectively; in the opposite case
, respectively; in the opposite case 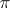 is called non-split (indecomposable). A non-split reducible representation
is called non-split (indecomposable). A non-split reducible representation  is not solely determined by its subrepresentation and quotient representation corresponding to a given invariant subspace, but also requires for its characterization certain one-dimensional cohomology classes of the group
is not solely determined by its subrepresentation and quotient representation corresponding to a given invariant subspace, but also requires for its characterization certain one-dimensional cohomology classes of the group 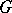 with coefficients in the
with coefficients in the 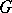 -module of bounded linear operators from the space of the quotient representation into the space of the representation.
-module of bounded linear operators from the space of the quotient representation into the space of the representation.
The most important general problems in the representation theory of topological groups are the description of all non-split representations of a given topological group and the study of the description (decomposition) of arbitrary representations of a topological group in terms of non-split ones. In both cases the problems are far from being completely solved (1991), but the results obtained still suffice to make the representation theory of topological groups a basis for abstract harmonic analysis (cf. Harmonic analysis, abstract), generalizing the theory of Fourier series and integrals, the spectral theory of unitary operators, the theory of Jordan normal forms and systems of ordinary differential equations with constant coefficients, as well as a basis for certain branches of ergodic theory, quantum mechanics, statistical physics, and field theory.
The most important branch of the representation theory of topological groups is the theory of unitary representations (cf. Unitary representation), which has many applications. A number of special properties simplify their study. In particular, the orthogonal complement to an invariant subspace of a unitary representation is invariant, and therefore every unitary representation is completely reducible. For unitary representations, the conditions of total irreducibility, (topological) irreducibility and operator-irreducibility are equivalent (but, in general, are weaker than the condition of algebraic irreducibility).
Another class of representations of topological groups which has various applications is that of finite-dimensional representations (cf. Finite-dimensional representation). The study of representations of this class is greatly facilitated by the relative simplicity of the functional-analytic problems as compared to the general case; in particular, an irreducible finite-dimensional representation is totally irreducible. However, the theory of finite-dimensional representations of topological groups has been developed satisfactorily (1991) only for certain classes of such groups (in particular, for semi-simple Lie groups and for the groups 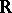 and
and 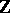 ). For many classes of groups, including the class of connected Lie groups, there is a complete description of the irreducible finite-dimensional representations.
). For many classes of groups, including the class of connected Lie groups, there is a complete description of the irreducible finite-dimensional representations.
The theory of representations has been mostly developed for locally compact groups. A most important property of the class of locally compact groups is that it coincides with the class of complete topological groups on which there is a non-zero right-invariant regular Borel measure 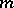 (cf. Haar measure). This allows one to add to the useful group algebras of a locally compact group
(cf. Haar measure). This allows one to add to the useful group algebras of a locally compact group 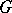 , the symmetric Banach algebra
, the symmetric Banach algebra 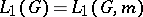 (under convolution), which plays a decisive role in the theory of bounded representations of a topological group
(under convolution), which plays a decisive role in the theory of bounded representations of a topological group 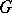 in Banach spaces (i.e. representations having bounded image). The formula
in Banach spaces (i.e. representations having bounded image). The formula
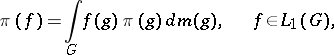 |
establishes a one-to-one correspondence between the bounded representations 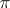 of a locally compact group
of a locally compact group 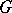 and the (continuous) representations
and the (continuous) representations 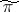 of the algebra
of the algebra 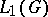 with the property that
with the property that 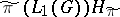 is dense in the space
is dense in the space 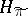 of the representation
of the representation 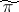 . Here, unitary representations of the group correspond to symmetric representations of
. Here, unitary representations of the group correspond to symmetric representations of 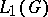 . Another property of locally compact groups is that their representations in barrelled locally convex spaces are jointly continuous.
. Another property of locally compact groups is that their representations in barrelled locally convex spaces are jointly continuous.
The theory of unitary representations of locally compact groups is the most fully developed branch of the representation theory of topological groups. Related to the existence of a Haar measure on locally compact groups is the possibility of studying the regular representation of 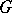 in
in 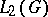 , which leads, in particular, to an analogue of the Plancherel formula for such groups, as well as to singling out the basic, complementary and discrete series of unitary representations of groups of the class considered (cf. Complementary series (of representations); Discrete series (of representations)). Important general problems in the theory of unitary representations are the problems of constructing irreducible representations and quotient representations, of decomposing representations into a direct integral, and of studying dual objects, and the problems of the theory of spherical functions, characters and harmonic analysis related to them, including the study of various group algebras.
, which leads, in particular, to an analogue of the Plancherel formula for such groups, as well as to singling out the basic, complementary and discrete series of unitary representations of groups of the class considered (cf. Complementary series (of representations); Discrete series (of representations)). Important general problems in the theory of unitary representations are the problems of constructing irreducible representations and quotient representations, of decomposing representations into a direct integral, and of studying dual objects, and the problems of the theory of spherical functions, characters and harmonic analysis related to them, including the study of various group algebras.
A subclass of the class of locally compact groups that is exceptionally rich in applications is the class of Lie groups. The theory of infinite-dimensional representations (cf. Infinite-dimensional representation) of Lie groups, including the representation theory of the classical groups, is one of the most quickly developing branches of the general representation theory of topological groups. A powerful method in the study of representations of Lie groups is the orbit method.
Another important subclass of the class of locally compact groups is the class of compact groups. The representation theory of compact groups is one of the most complete branches of the general representation theory of topological groups, and is a tool in the study of representations of topological groups containing compact subgroups. An important branch of the representation theory of compact groups concerns the decomposition of restrictions to subgroups, and the decomposition of tensor products of concrete representations of compact Lie groups. A part of the representation theory of compact groups with many applications in algebra and analysis is the theory of representations of finite groups.
Like in the above-mentioned study of non-split representations of topological groups, even the simpler problem of describing the intertwining of totally irreducible representations, related with a corresponding cohomology theory, has only been solved (1991) for certain groups, despite its importance in the harmonic analysis on groups. In fact, in terms of non-split representations (more precisely, in terms of representations participating in the analytic extension of the corresponding basic series) for certain Lie groups (respectively, Chevalley groups) one has obtained analogues of the Paley–Wiener theorem, giving a description of the image of the group algebra of infinitely-differentiable (respectively, locally finite) functions with compact support on the group under Fourier transformation (i.e. under the mapping 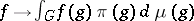 ,
,  , assigning to a function on the group an operator-valued function on a set of representatives of the space of equivalence classes of representations of this group). The more special problem of describing all totally-irreducible representations of a given group has been solved (1991) only for locally compact groups whose quotient group by the centre is compact (a totally-irreducible representation of such a group is finite-dimensional and the set of these representations suffices for obtaining an analogue to the Paley–Wiener theorem) and for certain linear Lie groups (including the complex semi-simple ones). As in the theory of unitary representations, in the theory of non-unitary representations one has likewise compiled a vast amount of material relating to concrete representations of certain particular groups and relating to applications to individual problems of harmonic analysis on such groups.
, assigning to a function on the group an operator-valued function on a set of representatives of the space of equivalence classes of representations of this group). The more special problem of describing all totally-irreducible representations of a given group has been solved (1991) only for locally compact groups whose quotient group by the centre is compact (a totally-irreducible representation of such a group is finite-dimensional and the set of these representations suffices for obtaining an analogue to the Paley–Wiener theorem) and for certain linear Lie groups (including the complex semi-simple ones). As in the theory of unitary representations, in the theory of non-unitary representations one has likewise compiled a vast amount of material relating to concrete representations of certain particular groups and relating to applications to individual problems of harmonic analysis on such groups.
A number of problems of the representation theory of topological groups is related to representations in spaces with an indefinite metric (cf. Space with an indefinite metric). A complete description of the irreducible representations in such spaces has been obtained for certain semi-simple Lie groups (this includes, in particular, their irreducible finite-dimensional representations). For these groups one has also found a decomposition of tensor products of certain irreducible representations of this type into irreducible unitary representations. The theory of operator-irreducible representations of semi-simple Lie groups in such spaces and the determination of the structures of their invariant subspaces is closely related with the analytic extension of the basic series of representations of these groups.
The representation theory of topological groups comprises the development of the theory of projective representations (cf. Projective representation), the generalization of the theory of representations of Lie groups (in particular, the orbit method) to locally compact groups of general type, and the theory of representations of topological groups that are not locally compact (the group of smooth functions on a manifold with values in a Lie group, the group of diffeomorphisms of a smooth manifold, infinite-dimensional analogues of the classical and other groups). The study of representations of such groups turned out to be related with probability theory (in particular, with the theory of Markov processes) and with problems in statistical physics. On the other hand, deep connections between the theory of representations of second-order matrix groups over locally compact fields and problems in number theory have been established.
References
| [1] | A.O. Barut, R. Raçzka, "Theory of group representations and applications" , 1–2 , PWN (1977) |
| [2] | N.Ya. Vilenkin, "Special functions and the theory of group representations" , Amer. Math. Soc. (1968) (Translated from Russian) |
| [3] | I.M. Gel'fand, M.I. Graev, I.I. Pyatetskii-Shapiro, "Generalized functions" , 6. Representation theory and automorphic functions , Saunders (1969) (Translated from Russian) |
| [4] | E. Jaquet, R. Langlands, "Automorphic forms on  " , 1–2 , Springer (1970–1972) " , 1–2 , Springer (1970–1972) |
| [5] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) |
| [6] | D.P. Zhelobenko, "Harmonic analysis of functions on semi-simple complex Lie groups" , Moscow (1974) (In Russian) |
| [7] | D.P. Zhelobenko, A.I. Shtern, "Representations of Lie groups" , Moscow (1983) (In Russian) |
| [8] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [9] | A.U. Klimyk, "Matrix elements and Clebsch–Gordan coefficients of group representations" , Kiev (1979) (In Russian) |
| [10] | S. Lang, " " , Addison-Wesley (1975) " , Addison-Wesley (1975) |
| [11] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [12] | M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) |
| [13] | S.A. Gaal, "Linear analysis and representation theory" , Springer (1973) |
| [14] | I.M. Gel'fand (ed.) , Lie groups and their representations , A. Hilger (1975) |
| [15] | G.W. Mackey, "Unitary group representations in physics, probability and number theory" , Benjamin/Cummings (1978) |
| [16] | G. Carmona (ed.) M. Vergne (ed.) , Non-commutative harmonic analysis (Marseille, 1978) , Lect. notes in math. , 728 , Springer (1979) |
Comments
See also the references to Representation of a group; Representation of a compact group.
A linear representation  of
of 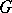 into
into 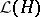 , the continuous linear operators on a topological vector space, is called algebraically irreducible if there are no non-trivial invariant subspaces; it is called irreducible or, to stress the topological context, topologically irreducible, if there are no non-trivial closed invariant subspaces; it is called totally irreducible, also called completely irreducible, if every element of
, the continuous linear operators on a topological vector space, is called algebraically irreducible if there are no non-trivial invariant subspaces; it is called irreducible or, to stress the topological context, topologically irreducible, if there are no non-trivial closed invariant subspaces; it is called totally irreducible, also called completely irreducible, if every element of 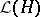 is the weak limit of a net consisting of linear combinations of operators
is the weak limit of a net consisting of linear combinations of operators 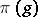 ,
, 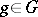 ; cf. [8], §7, [1], Chapt. V, §3; [13], Chapt. IV, §2.
; cf. [8], §7, [1], Chapt. V, §3; [13], Chapt. IV, §2.
Representation of a topological group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Representation_of_a_topological_group&oldid=18500