Difference between revisions of "Plessner theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | p0728801.png | ||
| + | $#A+1 = 44 n = 1 | ||
| + | $#C+1 = 44 : ~/encyclopedia/old_files/data/P072/P.0702880 Plessner theorem | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | One of the basic results in the theory of [[Boundary properties of analytic functions|boundary properties of analytic functions]]. Let $ f( z) $ | |
| + | be a meromorphic function in the unit disc $ D = \{ {z \in \mathbf C } : {| z | < 1 } \} $ | ||
| + | and let $ \Delta = \Delta ( e ^ {i \theta } ) $ | ||
| + | be the open angle with vertex $ e ^ {i \theta } $ | ||
| + | on the circle $ \Gamma = \{ {z \in \mathbf C } : {| z | = 1 } \} $ | ||
| + | formed by two chords of $ D $ | ||
| + | passing through $ e ^ {i \theta } $. | ||
| + | The point $ e ^ {i \theta } $ | ||
| + | is called a Plessner point (or it is said that $ e ^ {i \theta } $ | ||
| + | has the Plessner property) if in every arbitrarily small angle $ \Delta $ | ||
| + | there exists a sequence $ \{ z _ {k} \} \subset \Delta $ | ||
| + | such that | ||
| − | + | $$ | |
| + | \lim\limits _ {k \rightarrow \infty } z _ {k} = e ^ {i \theta } ,\ \ | ||
| + | \lim\limits _ {k \rightarrow \infty } f( z _ {k} ) = w | ||
| + | $$ | ||
| − | + | for every value $ w $ | |
| + | in the extended complex plane $ \overline{\mathbf C}\; $. | ||
| + | The point $ e ^ {i \theta } $ | ||
| + | is called a Fatou point for $ f( z) $ | ||
| + | if there exists a single unique limit | ||
| − | + | $$ | |
| + | \lim\limits f( z) = A | ||
| + | $$ | ||
| − | + | as $ z $ | |
| + | tends to $ e ^ {i \theta } $ | ||
| + | within any angle $ \Delta $. | ||
| + | Plessner's theorem [[#References|[1]]]: Almost-all points on $ \Gamma $ | ||
| + | with respect to the Lebesgue measure on $ \Gamma $ | ||
| + | are either Fatou points or Plessner points. | ||
| − | + | It is also known that the set $ P( f ) $ | |
| + | of all Plessner points has type $ G _ \delta $ | ||
| + | on $ \Gamma $. | ||
| + | Examples have been constructed of analytic functions in $ D $ | ||
| + | for which $ P( f ) $ | ||
| + | is dense on $ \Gamma $ | ||
| + | and has arbitrary given Lebesgue measure $ \mathop{\rm mes} P( f ) = m $, | ||
| + | $ 0 \leq m < 2 \pi $[[#References|[3]]]. Plessner's theorem applies to any meromorphic function $ f( z) $ | ||
| + | in any simply-connected domain $ D $ | ||
| + | with a rectifiable boundary $ \Gamma $. | ||
| + | In that case, $ \zeta \in \Gamma $ | ||
| + | is a Fatou point if the following limit exists (cf. also [[Cluster set|Cluster set]]): | ||
| + | |||
| + | $$ | ||
| + | \lim\limits f( z) = A,\ \ | ||
| + | z \in D, | ||
| + | $$ | ||
| + | |||
| + | as $ z \rightarrow \zeta $ | ||
| + | along any non-tangential path; the definition of a Plessner point $ \zeta \in \Gamma $ | ||
| + | must be altered in such a way that one considers angles $ \Delta $ | ||
| + | with vertex $ \zeta $ | ||
| + | and sides forming angles less than $ \pi /2 $ | ||
| + | with the normal to $ \Gamma $ | ||
| + | at $ \zeta $[[#References|[2]]]. | ||
Meier's theorem is an analogue of Plessner's theorem in terms of categories of sets (cf. [[Meier theorem|Meier theorem]]). | Meier's theorem is an analogue of Plessner's theorem in terms of categories of sets (cf. [[Meier theorem|Meier theorem]]). | ||
| Line 19: | Line 76: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.I. Plessner, "Über das Verhalten analytischer Funktionen auf dem Rande des Definitionsbereiches" ''J. Reine Angew. Math.'' , '''158''' (1928) pp. 219–227</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.J. Lohwater, "The boundary behaviour of analytic functions" ''Itogi Nauk. i Tekhn. Mat. Anal.'' , '''10''' (1973) pp. 99–259 (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.I. Plessner, "Über das Verhalten analytischer Funktionen auf dem Rande des Definitionsbereiches" ''J. Reine Angew. Math.'' , '''158''' (1928) pp. 219–227</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.J. Lohwater, "The boundary behaviour of analytic functions" ''Itogi Nauk. i Tekhn. Mat. Anal.'' , '''10''' (1973) pp. 99–259 (In Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Angles of the form | + | Angles of the form $ \Delta $ |
| + | are called Stolz angles. | ||
A good reference is [[#References|[a3]]], to which [[#References|[3]]] is a Russian sequel. | A good reference is [[#References|[a3]]], to which [[#References|[3]]] is a Russian sequel. | ||
| − | Plessner's theorem has a complete analogue for the unit ball in | + | Plessner's theorem has a complete analogue for the unit ball in $ \mathbf C ^ {n} $, |
| + | cf. [[#References|[a1]]]: Every holomorphic function on the unit ball decomposes the boundary into three measurable sets, as in the classical case. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rudin, "Function theory in the unit ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072880/p07288045.png" />" , Springer (1981)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1975)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 9</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> K. Noshiro, "Cluster sets" , Springer (1960)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rudin, "Function theory in the unit ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072880/p07288045.png" />" , Springer (1981)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1975)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 9</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> K. Noshiro, "Cluster sets" , Springer (1960)</TD></TR></table> | ||
Latest revision as of 08:06, 6 June 2020
One of the basic results in the theory of boundary properties of analytic functions. Let $ f( z) $
be a meromorphic function in the unit disc $ D = \{ {z \in \mathbf C } : {| z | < 1 } \} $
and let $ \Delta = \Delta ( e ^ {i \theta } ) $
be the open angle with vertex $ e ^ {i \theta } $
on the circle $ \Gamma = \{ {z \in \mathbf C } : {| z | = 1 } \} $
formed by two chords of $ D $
passing through $ e ^ {i \theta } $.
The point $ e ^ {i \theta } $
is called a Plessner point (or it is said that $ e ^ {i \theta } $
has the Plessner property) if in every arbitrarily small angle $ \Delta $
there exists a sequence $ \{ z _ {k} \} \subset \Delta $
such that
$$ \lim\limits _ {k \rightarrow \infty } z _ {k} = e ^ {i \theta } ,\ \ \lim\limits _ {k \rightarrow \infty } f( z _ {k} ) = w $$
for every value $ w $ in the extended complex plane $ \overline{\mathbf C}\; $. The point $ e ^ {i \theta } $ is called a Fatou point for $ f( z) $ if there exists a single unique limit
$$ \lim\limits f( z) = A $$
as $ z $ tends to $ e ^ {i \theta } $ within any angle $ \Delta $. Plessner's theorem [1]: Almost-all points on $ \Gamma $ with respect to the Lebesgue measure on $ \Gamma $ are either Fatou points or Plessner points.
It is also known that the set $ P( f ) $ of all Plessner points has type $ G _ \delta $ on $ \Gamma $. Examples have been constructed of analytic functions in $ D $ for which $ P( f ) $ is dense on $ \Gamma $ and has arbitrary given Lebesgue measure $ \mathop{\rm mes} P( f ) = m $, $ 0 \leq m < 2 \pi $[3]. Plessner's theorem applies to any meromorphic function $ f( z) $ in any simply-connected domain $ D $ with a rectifiable boundary $ \Gamma $. In that case, $ \zeta \in \Gamma $ is a Fatou point if the following limit exists (cf. also Cluster set):
$$ \lim\limits f( z) = A,\ \ z \in D, $$
as $ z \rightarrow \zeta $ along any non-tangential path; the definition of a Plessner point $ \zeta \in \Gamma $ must be altered in such a way that one considers angles $ \Delta $ with vertex $ \zeta $ and sides forming angles less than $ \pi /2 $ with the normal to $ \Gamma $ at $ \zeta $[2].
Meier's theorem is an analogue of Plessner's theorem in terms of categories of sets (cf. Meier theorem).
References
| [1] | A.I. Plessner, "Über das Verhalten analytischer Funktionen auf dem Rande des Definitionsbereiches" J. Reine Angew. Math. , 158 (1928) pp. 219–227 |
| [2] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [3] | A.J. Lohwater, "The boundary behaviour of analytic functions" Itogi Nauk. i Tekhn. Mat. Anal. , 10 (1973) pp. 99–259 (In Russian) |
Comments
Angles of the form $ \Delta $ are called Stolz angles.
A good reference is [a3], to which [3] is a Russian sequel.
Plessner's theorem has a complete analogue for the unit ball in $ \mathbf C ^ {n} $, cf. [a1]: Every holomorphic function on the unit ball decomposes the boundary into three measurable sets, as in the classical case.
References
| [a1] | W. Rudin, "Function theory in the unit ball in 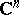 " , Springer (1981) " , Springer (1981) |
| [a2] | M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1975) |
| [a3] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 9 |
| [a4] | K. Noshiro, "Cluster sets" , Springer (1960) |
Plessner theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Plessner_theorem&oldid=48190