Piecewise-linear topology
The branch of topology dealing with polyhedra. By a polyhedron one means, first and foremost, a subset of a topological vector space which is a finite or locally finite union of convex polytopes of bounded dimension, but also topological polyhedra with a fixed piecewise-linear structure (see below). By locally finite one means that each point in the ambient space has a neighbourhood which intersects only finitely many elements of the union. The concept of a polyhedron lies midway between the concepts of a topological space and a simplicial complex (the latter is introduced in order to permit a more constructive study first of spaces homeomorphic to polyhedra and subsequently of more general spaces). A space homeomorphic to a polyhedron is called a topological polyhedron (t-polyhedron). The class of t-polyhedra contains the most important objects of finite-dimensional topology — primarily smoothable manifolds.
With an eye to finitization of the study of polyhedra, one considers the four categories $ \mathfrak T , {\mathcal P} , {\mathcal K} , {\mathcal A} $. The objects of $ \mathfrak T $ are the t-polyhedra; its morphisms are continuous mappings. The objects of $ {\mathcal P} $ are the polyhedra, and its morphisms are piecewise-linear mappings (pl-mappings), i.e. mappings which linearly transform the convex polytopes of some covering of the domain into polytopes of some covering of the range. The objects in $ {\mathcal K} $ are the simplicial complexes, i.e. polyhedra with a fixed regular covering by simplices (a covering such that two simplices may intersect only along a common face), the morphisms in $ {\mathcal K} $ are simplicial mappings, i.e. pl-mappings which linearly transform each simplex of the domain onto some simplex of the range. Finally, $ {\mathcal A} $ consists of abstract complexes (a-complexes) and their simplicial mappings. An a-complex in $ {\mathcal A} $ is an at most countable set $ \overline{A}\; $ with a distinguished system of finite subsets of bounded cardinality, called simplices, which satisfy the following conditions: 1) for each simplex $ \sigma $ the distinguished system also contains all subsets of the simplex — the faces of $ \sigma $; and 2) each simplex is a face of at most finitely many other simplices. A mapping of sets possessing the structure of a-complexes is said to be simplicial if it takes simplices of the domain onto simplices of the range. The dimension of a simplex in an a-complex is one less than the number of its elements. Each element of the set $ \overline{A}\; $ is a face of the complex $ A $ and is called a vertex of $ A $. It is convenient to assume that each a-complex contains the empty simplex, denoted by 1.
There exist forgetful functors
$$ \mathfrak T \leftarrow ^ { t } \ {\mathcal P} \leftarrow ^ { p } \ {\mathcal K} \rightarrow ^ { a } \ {\mathcal A} . $$
In fact, a polyhedron defines a topological space, and a pl-mapping is continuous, this gives $ t $; $ t ( P) $ is called the space of the polyhedron $ P $. Each complex defines a polyhedron, and a simplicial mapping of complexes is a pl-mapping, this gives $ p $; $ p ( K) $ is called the body or skeleton of the complex and is denoted by $ | K | $. Finally, the set of vertices of a complex $ K $ contains distinguished subsets — the sets of vertices of the simplices in $ K $, and this defines an a-complex; a simplicial mapping of complexes defines a simplicial mapping of the corresponding a-complexes. This gives $ a $, and $ a ( K) $ is called the scheme of the complex $ K $. These functors do not have natural inverses. However, they become equivalences if one goes over to suitable quotient categories. The natural isomorphisms are called, respectively, homeomorphisms in $ \mathfrak T $, pl-homeomorphisms in $ {\mathcal P} $, and simplicial isomorphisms in $ {\mathcal K} $ and $ {\mathcal A} $. For every a-complex $ A $ one can define a realization as follows. In a topological vector space $ R $, choose a set of points $ b _ {i} $ that correspond one-to-one with the vertices of $ A $ and are moreover in general position in $ R $( this may be done if e.g. the dimension of $ R $ exceeds twice that of $ A $), in such a way that only finitely many points lie in a bounded region of the space. Every set of points $ b _ {i} $ corresponding to the same simplex in $ A $ spans a certain simplex in $ R $; the union of all such simplices yields a complex with as scheme precisely $ A $— a realization of $ A $. All realizations of the same a-complex are isomorphic, so that the functor $ a $ establishes a one-to-one correspondence between the classes of isomorphic complexes in $ {\mathcal K} $ and in $ {\mathcal A} $. Any polyhedron $ P $ is the skeleton of some complex $ K $, in which case $ K $ is known as a rectilinear triangulation of $ P $, or simply a triangulation; a scheme of $ K $ is known as an abstract triangulation of $ P $. Given a pl-mapping $ f: P \rightarrow Q $ there exist triangulations $ K $ for $ P $ and $ L $ for $ Q $ so that $ f $ is a simplicial mapping of $ K $ into $ L $. Different triangulations of a polyhedron need not be isomorphic, so that one obtains a coarser equivalence relation in $ {\mathcal K} $. A refinement of a complex $ K _ {1} $ is defined as a complex $ K _ {2} $ such that $ | K _ {2} | = | K _ {1} | $ and such that each simplex of $ K _ {2} $ is a subset of some simplex of $ K _ {1} $. A complex $ K $ is combinatorially equivalent to $ K ^ \prime $ if $ K $ and $ K ^ \prime $ possess isomorphic refinements. Two complexes $ K $ and $ K ^ \prime $ are combinatorially equivalent if and only if $ | K | $ is pl-homeomorphic to $ | K ^ \prime | $. In other words, the functor $ p $ establishes a natural correspondence between the classes of combinatorially equivalent complexes and pl-homeomorphic polyhedra. The functor $ t $ is epimorphic (by definition). A polyhedron $ P $ is known as a rectilinear realization of the t-polyhedron $ t ( P) $. The assertion that any two realizations of a t-polyhedron are pl-homeomorphic is known as the fundamental conjecture of combinatorial topology (the Hauptvermutung); it has been proved false [3]. It is thus meaningful to define pl-structures on t-polyhedra: A pl-structure is given by a homeomorphism $ \tau : T \rightarrow P $ of a t-polyhedron onto a polyhedron, with two homeomorphisms $ \tau _ {1} : T \rightarrow P _ {1} $ and $ \tau _ {2} : T \rightarrow P _ {2} $ considered to define the same structure if $ \tau _ {1} \tau _ {2} ^ {-} 1 $ is a pl-homeomorphism; $ \tau _ {1} $ and $ \tau _ {2} $ define equivalent (but not necessarily identical) structures if $ P _ {1} $ and $ P _ {2} $ are pl-homeomorphic. A t-polyhedron with a fixed pl-structure is also called a polyhedron. Finally, the relation of combinatorial equivalence in $ {\mathcal K} $ implies, via the functor $ a $, a new equivalence relation in $ {\mathcal A} $. In order to formulate this relation intrinsically in $ {\mathcal A} $, it is convenient to define the operation of stellar subdivision, as follows. The join (or union) of two simplices $ \sigma _ {1} ^ {n _ {1} } $ and $ \sigma _ {2} ^ {n _ {2} } $ whose vertices are in general position in the vector space $ R $ is defined as their convex hull; the latter is an $ ( n _ {1} + n _ {2} - 1) $- dimensional simplex, denoted by $ \sigma _ {1} * \sigma _ {2} $. The join of $ \sigma $ with the empty simplex 1 is $ \sigma $. The join of two complexes $ K _ {1} $ and $ K _ {2} $, positioned in a topological vector space $ R $ such that each simplex of $ K _ {1} $ is in general position with each simplex of $ K _ {2} $, is defined as the complex formed by the pairwise joins of the simplices of $ K _ {1} $ with the simplices of $ K _ {2} $( it is assumed that 1 is in both $ K _ {1} $ and $ K _ {2} $). The star of a simplex $ \sigma $ in a complex $ K $ is defined as the subcomplex $ \mathop{\rm St} _ {K} \sigma $ consisting of all closed simplices of which $ \sigma $ is a face. The star may be conceived of as the join of $ \sigma $ with a certain complex $ \mathop{\rm lk} _ {K} \sigma $, known as the link of $ \sigma $ in $ K $ and consisting of those simplices in the star that do not intersect $ \sigma $. Let $ x $ be any point in the interior of $ \sigma $. In $ K $, replace all simplices of the star by simplices $ x * \sigma _ {1} * \sigma _ {2} $, where $ \sigma _ {1} $ is a simplex in $ \mathop{\rm lk} _ {K} \sigma $ and $ \sigma _ {2} $ is a face of $ \sigma $; all other simplices of $ K $ are retained. The result is a subdivision of $ K $, called its subdivision with centre $ \sigma $ and denoted by $ \sigma K $. Two complexes are combinatorially equivalent if and only if they possess isomorphic subdivisions obtained via successive stellar subdivisions and inverses of such (Alexander's theorem, [4]).
The concept of a stellar subdivision carries over to the category $ {\mathcal A} $. To do this, one expresses the complexes as polynomials of a special type: The variables are the vertices of the complex, and the monomials are its simplices, including 1. Repeated simplices occurring when polynomials are added are replaced by a single monomial. Multiplication of polynomials (defined only if the factors have no common variables) is interpreted as the union of the corresponding complexes. Let $ \sigma $ be a fixed simplex in a complex $ A $, and write $ A $ as $ A = \sigma * \mathop{\rm lk} _ {A} \sigma + A _ {1} $, where $ \sigma $ is taken out of the brackets from the union of all monomials that contain it (i.e. all monomials in $ \mathop{\rm St} _ {A} \sigma $). Inside the brackets, the link of $ \sigma $ remains; $ A _ {1} $ is the join of all other simplices. Replacing $ \sigma $ by $ x * \partial \sigma $, where $ \partial \sigma $ is the union of the faces of $ \sigma $( except for $ \sigma $ itself), including 1, one obtains a new complex $ \sigma A = x * \partial \sigma * \mathop{\rm lk} _ {A} \sigma + A _ {1} $. The transformation $ A \rightarrow \sigma A $ and $ \sigma A $ itself are known as an (abstract) stellar subdivision of $ A $. The stellar subdivision operations in $ {\mathcal K} $ and in $ {\mathcal A} $ are compatible with the functor $ a $, so that one can represent $ {\mathcal A} $ as a formal system with a countable alphabet whose constructive objects are the monomials just described and whose elementary transformations (from one object to another) are the stellar subdivisions. One can thus formulate algorithmic solvability problems in $ A $. For example, the problem of combinatorial equivalence of a-complexes (and consequently also of pl-homeomorphism of polyhedra) is unsolvable (Markov's theorem, [5]).
The original goal of the finitistic approach to complexes was to introduce invariants: An invariant is defined with respect to triangulation, and its invariance is verified only under elementary transformations (the model for this procedure was the definition of the Euler characteristic). However, this method has not achieved much popularity; firstly, owing to the invalidity of the Hauptvermutung it does not yield a proof of the topological invariance, and, secondly, the actual computation of triangulation invariants is often a hopeless task. The method has been applied, more or less systematically, in the topology of three-dimensional manifolds (cf. Topology of manifolds; Three-dimensional manifold) and in knot theory. In homotopy theory it has produced the technique of cellular decompositions (cf. CW-complex). A development of the idea of an a-complex has led to a theory of semi-simplicial complexes, which help to avoid unnecessary topological complications in homotopy theory (cf. Semi-simplicial complex).
The basic objects of piecewise-linear topology are the pl-manifolds, which serve as an important connecting link between differential and topological manifolds. The concept of a manifold can be defined naturally in each of the four categories $ \mathfrak T , {\mathcal P} , {\mathcal K} , {\mathcal A} $. In $ \mathfrak T $ it is simply the concept of a triangulable topological manifold; in $ {\mathcal P} $ one has pl-manifolds — polyhedra each point of which has a neighbourhood that is pl-homeomorphic to a cube of suitable dimension; in $ {\mathcal K} $ and in $ {\mathcal A} $ one considers combinatorial and formal manifolds, respectively — complexes (a-complexes) in which the stars of the vertices are combinatorially equivalent to the standard triangulation of a simplex, consisting of the simplex itself and all its faces. The Hauptvermutung is false in the class of pl-manifolds as well [6]. An example has been devised of a non-combinatorial triangulation of a topological manifold (see [7], [8]) in which the imbeddings of certain simplices are not locally flat. If one assumes that all simplices are locally flat and, in addition, accepts the truth of the Poincaré conjecture in dimensions 3 and 4, one can prove that a triangulation of a manifold is a combinatorial manifold. Finally, it is not known (1989) whether an arbitrary (metrizable) manifold is triangulable, though examples have been presented of manifolds with no combinatorial triangulation [6].
References
| [1] | C.P. Rourke, B.J. Sanderson, "Introduction to piecewise-linear topology" , Springer (1972) |
| [2] | J.R. Munkres, "Elementary differential topology" J.W. Milnor (ed.) J. Stasheff (ed.) , Characteristic classes , Princeton Univ. Press (1974) pp. 270–359 |
| [3] | J. Milnor, "Two complexes which are homeomorphic but combinatorially distinct" Ann. of Math. , 74 (1961) pp. 575–590 |
| [4] | J.W. Alexander, "Combinatorial analysis situs" Trans. Amer. Math. Soc. , 28 (1926) pp. 301–329 |
| [5] | A.A. Markov, "The unsolvability of the homeomorphism problem" Dokl. Akad. Nauk SSSR , 121 : 2 (1958) pp. 218–220 (In Russian) |
| [6] | R. Kirby, L. Siebenmann, "On the triangulation of manifolds and the Hauptvermutung" Bull. Amer. Math. Soc. , 75 (1969) pp. 742–749 |
| [7] | R.D. Edwards, "The double suspension of a certain homology 3-sphere in 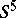 " Notices Amer. Math. Soc. , 22 : 2 (1975) pp. A-334 " Notices Amer. Math. Soc. , 22 : 2 (1975) pp. A-334 |
| [8] | J.W. Cannon, "Shrinking cell-like decompositions of manifolds. Codimension three" Ann. of Math. , 10 (1979) pp. 83–112 |
Comments
References
| [a1] | J.R. Stallings, "Lectures on polyhedral topology" , Tata Inst. (1967) |
| [a2] | E.C. Zeeman, "Seminar on combinatorial topology" , IHES (1963) |
| [a3] | R.C. Kirby, L.C. Siebenmann, "Foundational essays on topological manifolds, smoothings, and triangulations" , Princeton Univ. Press (1977) pp. 155–213 |
Piecewise-linear topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Piecewise-linear_topology&oldid=48181