Parallel straight lines
in Euclidean geometry
Lines that lie in one plane and that do not intersect. In absolute geometry there passes through a point not lying on a given line at least one line that does not intersect the given one. In Euclidean geometry there is only one such line. This fact is equivalent to Euclid's fifth postulate (on parallels). In Lobachevskii geometry in the plane there pass through a point $ C $( see Fig.) outside a given line $ AB $ infinitely-many lines that do not intersect $ AB $. Of these only two are called parallel to $ AB $. A line $ CE $ is said to be parallel to $ AB $ in the direction from $ A $ to $ B $ if: 1) $ B $ and $ E $ lie on the same side of $ AC $; 2) $ CE $ does not intersect $ AB $; and 3) every ray within the angle $ ACE $ intersects the line $ AB $. The line $ CF $ parallel to $ AB $ in the direction from $ B $ to $ A $ is defined similarly.
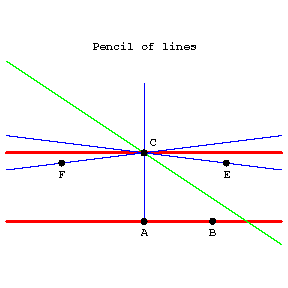
Figure: p071380a
Comments
References
| [a1] | H.S.M. Coxeter, "Parallel lines" Canad. Math. Bulletin , 21 : 4 (1978) pp. 385–397 |
| [a2] | M. Greenberg, "Euclidean and non-Euclidean geometries" , Freeman (1974) |
| [a3] | D. Hilbert, "Grundlagen der Geometrie" , Teubner, reprint (1968) |
Parallel straight lines. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parallel_straight_lines&oldid=48117