Difference between revisions of "Operator"
m (structure) |
m (→Graph: some tex) |
||
| Line 28: | Line 28: | ||
===Graph === | ===Graph === | ||
| − | The set | + | The set $\Gamma(A)\subset X\times Y$ defined by the relation |
| − | + | \begin{equation} | |
| − | + | \Gamma(A) = \{(x,Ax) : x\in \operatorname{Dom}(A)\} | |
| − | + | \end{equation} | |
| − | is called the graph of the operator | + | is called the graph of the operator $A$. |
| − | + | Let $X$ and $Y$ be topological vector spaces; an operator from $X$ into $Y$ is called a [[Closed operator|closed operator]] if its graph is closed. The concept of a closed operator is particularly useful in the case of linear operators with a dense domain of definition. | |
| − | Let | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | The concept of a graph allows one to generalize the concept of an operator: Any subset $A$ in $X\times Y$ is called a multi-valued operator from $X$ into $Y$; if $X$ and $Y$ are vector spaces, then a linear subspace in $X\times Y$ is called a multi-valued linear operator; the set | ||
| + | \begin{equation} | ||
| + | D(A) = \{x\in X : \text{ there exists an } y\in Y \text{ such that } (x, y)\in A \} | ||
| + | \end{equation} | ||
is called the domain of definition of the multi-valued operator. | is called the domain of definition of the multi-valued operator. | ||
| − | If | + | If $X$ is a vector space over a field $\mathcal K$ and $Y = \mathcal K$, then an everywhere-defined operator from $X$ into $Y$ is called a [[Functional|functional]] on $X$. |
If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350116.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350117.png" /> are locally convex spaces, then an operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350118.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350119.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350120.png" /> with a dense domain of definition in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350121.png" /> has an [[Adjoint operator|adjoint operator]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350122.png" /> with a dense domain of definition in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350123.png" /> (with the weak topology) if, and only if, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350124.png" /> is a closed operator. | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350116.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350117.png" /> are locally convex spaces, then an operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350118.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350119.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350120.png" /> with a dense domain of definition in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350121.png" /> has an [[Adjoint operator|adjoint operator]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350122.png" /> with a dense domain of definition in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350123.png" /> (with the weak topology) if, and only if, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068350/o068350124.png" /> is a closed operator. | ||
Revision as of 04:54, 23 December 2012
A mapping of one set into another, each of which has a certain structure (defined by algebraic operations, a topology, or by an order relation). The general definition of an operator coincides with the definition of a mapping or function. Let $X$ and $Y$ be two sets. A rule or correspondence which assigns a uniquely defined element $A(x)\in Y$ to every element $x$ of a subset $D\subset X$ is called an operator $A$ from $X$ into $Y$. \begin{equation} A:D\to Y, \qquad \text{where } D \subset X. \end{equation} The term operator is mostly used in the case where $X$ and $Y$ are vector spaces. The expression $A(x)$ is often written as $Ax$.
Definitions and Notations
- The subset $D$ is called the domain of definition of the operator $A$ and is denoted by $\operatorname{Dom}(A)$; the set $\{A(x) : x\in D\}$ is called the domain of values of the operator $A$ (or its range) and is denoted by $\operatorname{R}(A)$.
- If $A$ is an operator from $X$ into $Y$ where $X=Y$, then $A$ is called an operator on $X$.
- If $\operatorname{Dom}(A)=X$, then $A$ is called an everywhere-defined operator.
- If $A_1$, $A_2$ are operators from $X_1$ into $Y_1$ and from $X_2$ into $Y_2$ with domains of definition $\operatorname{Dom}(A_1)$ and $\operatorname{Dom}(A_2)$, respectively, such that $\operatorname{Dom}(A_1)\subset\operatorname{Dom}(A_2)$ and $A_1x=A_2x$ for all $x\in\operatorname{Dom}(A_1)$, then if $X_1=X_2$, $Y_1=Y_2$, the operator $A_1$ is called a compression or restriction of the operator $A_2$, while $A_2$ is called an extension of $A_1$; if $X_1\subset X_2$, $A_2$ is called an extension of $A_1$ exceeding $X_1$.
- If $X$ and $Y$ are vector spaces, then in the set of all operators from $X$ into $Y$ it is possible to single out the class of linear operators (cf. Linear operator); the remaining operators from $X$ into $Y$ are called non-linear operators.
- If $X$ and $Y$ are topological vector spaces, then in the set of operators from $X$ into $Y$ the class of continuous operators (cf. Continuous operator) can be naturally singled out, so are the class of bounded linear operators $A$ (operators $A$ such that the image of any bounded set in $X$ is bounded in $Y$) and the class of compact linear operators (i.e. operators such that the image of any bounded set in $X$ is pre-compact in $Y$, cf. Compact operator).
- If $X$ and $Y$ are locally convex spaces, then it is natural to examine different topologies on $X$ and $Y$; an operator is said to be semi-continuous if it defines a continuous mapping from the space $X$ (with the initial topology) into the space $Y$ with the weak topology (the concept of semi-continuity is mainly used in the theory of non-linear operators); an operator is said to be strongly continuous if it is continuous as a mapping from $X$ with the boundedly weak topology into the space $Y$; an operator is called weakly continuous if it defines a continuous mapping from $X$ into $Y$ where $X$ and $Y$ have the weak topology. Compact operators are often called completely-continuous operators. Sometimes the term "competely-continuous operator" is used instead of "strongly-continuous operator" , or to denote an operator which maps any weakly-convergent sequence to a strongly-convergent one; if $X$ and $Y$ are reflexive Banach spaces, then these conditions are equivalent to the compactness of the operator. If an operator is strongly continuous, then it is weakly continuous.
Connection with Equations
Many equations in function spaces or abstract spaces can be expressed in the form $Ax=y$, where $y\in Y$, $x \in X$; $y$ is given, $x$ is unknown and $A$ is an operator from $X$ into $Y$. The assertion of the existence of a solution to this equation for any right-hand side $y\in Y$ is equivalent to the assertion that the range of the operator $A$ is the whole space $Y$; the assertion that the equation $Ax=y$ has a unique solution for any $y\in\operatorname{R}(A)$ means that $A$ is a one-to-one mapping from $\operatorname{Dom}(A)$ onto $\operatorname{R}(A)$.
Graph
The set $\Gamma(A)\subset X\times Y$ defined by the relation \begin{equation} \Gamma(A) = \{(x,Ax) : x\in \operatorname{Dom}(A)\} \end{equation} is called the graph of the operator $A$. Let $X$ and $Y$ be topological vector spaces; an operator from $X$ into $Y$ is called a closed operator if its graph is closed. The concept of a closed operator is particularly useful in the case of linear operators with a dense domain of definition.
The concept of a graph allows one to generalize the concept of an operator: Any subset $A$ in $X\times Y$ is called a multi-valued operator from $X$ into $Y$; if $X$ and $Y$ are vector spaces, then a linear subspace in $X\times Y$ is called a multi-valued linear operator; the set \begin{equation} D(A) = \{x\in X : \text{ there exists an } y\in Y \text{ such that } (x, y)\in A \} \end{equation} is called the domain of definition of the multi-valued operator.
If $X$ is a vector space over a field $\mathcal K$ and $Y = \mathcal K$, then an everywhere-defined operator from $X$ into $Y$ is called a functional on $X$.
If 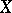 and
and 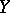 are locally convex spaces, then an operator
are locally convex spaces, then an operator 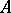 from
from 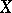 into
into 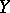 with a dense domain of definition in
with a dense domain of definition in 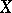 has an adjoint operator
has an adjoint operator 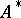 with a dense domain of definition in
with a dense domain of definition in 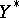 (with the weak topology) if, and only if,
(with the weak topology) if, and only if, 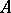 is a closed operator.
is a closed operator.
Examples of operators.
1) The operator assigning the element 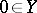 to any element
to any element 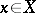 (the zero operator).
(the zero operator).
2) The operator mapping each element 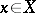 to the same element
to the same element 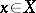 (the identity operator on
(the identity operator on 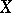 , written as
, written as 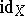 or
or 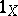 ).
).
3) Let 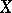 be a vector space of functions on a set
be a vector space of functions on a set 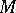 , and let
, and let 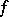 be a function on
be a function on 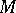 ; the operator on
; the operator on 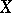 with domain of definition
with domain of definition
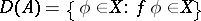 |
and acting according to the rule
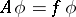 |
if 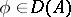 , is called the operator of multiplication by a function;
, is called the operator of multiplication by a function; 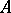 is a linear operator.
is a linear operator.
4) Let 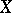 be a vector space of functions on a set
be a vector space of functions on a set 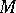 , and let
, and let 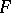 be a mapping from the set
be a mapping from the set 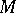 into itself; the operator on
into itself; the operator on 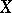 with domain of definition
with domain of definition
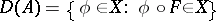 |
and acting according to the rule
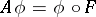 |
if 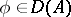 , is a linear operator.
, is a linear operator.
5) Let 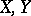 be vector spaces of real measurable functions on two measure spaces
be vector spaces of real measurable functions on two measure spaces 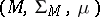 and
and 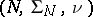 , respectively, and let
, respectively, and let 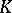 be a function on
be a function on 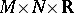 , measurable with respect to the product measure
, measurable with respect to the product measure 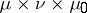 , where
, where 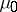 is Lebesgue measure on
is Lebesgue measure on 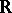 , and continuous in
, and continuous in 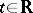 for any fixed
for any fixed 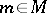 ,
, 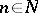 . The operator from
. The operator from 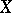 into
into 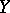 with domain of definition
with domain of definition  , which exists for almost-all
, which exists for almost-all 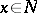 and
and 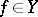 , and acting according to the rule
, and acting according to the rule 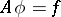 if
if 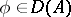 , is called an integral operator; if
, is called an integral operator; if
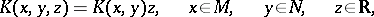 |
then 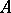 is a linear operator.
is a linear operator.
6) Let 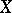 be a vector space of functions on a differentiable manifold
be a vector space of functions on a differentiable manifold 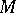 , let
, let 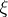 be a vector field on
be a vector field on 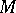 ; the operator
; the operator  on
on 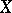 with domain of definition
with domain of definition
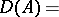 |
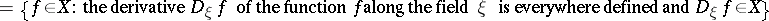 |
and acting according to the rule 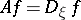 if
if 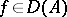 , is called a differentiation operator;
, is called a differentiation operator; 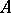 is a linear operator.
is a linear operator.
7) Let 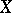 be a vector space of functions on a set
be a vector space of functions on a set 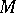 ; an everywhere-defined operator assigning to a function
; an everywhere-defined operator assigning to a function 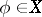 the value of that function at a point
the value of that function at a point 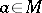 , is a linear functional on
, is a linear functional on 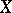 ; it is called the
; it is called the 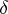 -function at the point
-function at the point  and is written as
and is written as 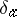 .
.
8) Let 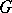 be a commutative locally compact group, let
be a commutative locally compact group, let 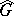 be the group of characters of the group
be the group of characters of the group 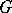 , let
, let 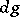 ,
, 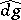 be the Haar measures on
be the Haar measures on 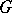 and
and 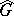 , respectively, and let
, respectively, and let
 |
The linear operator 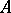 from
from 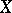 into
into 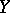 assigning to a function
assigning to a function  the function
the function 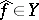 defined by the formula
defined by the formula
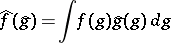 |
is everywhere defined if the convergence of the integral is taken to be mean-square convergence.
If 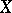 and
and 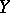 are topological vector spaces, then the operators in examples 1) and 2) are continuous; if in example 3) the space
are topological vector spaces, then the operators in examples 1) and 2) are continuous; if in example 3) the space 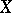 is
is 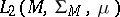 , where
, where 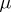 is a measure on
is a measure on 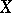 , then the operator of multiplication by a bounded measurable function is closed and has a dense domain of definition; if in example 5) the space
, then the operator of multiplication by a bounded measurable function is closed and has a dense domain of definition; if in example 5) the space 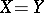 is a Hilbert space
is a Hilbert space 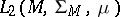 and
and 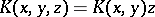 , where
, where 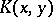 belongs to
belongs to 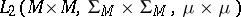 , then
, then 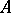 is compact; if in example 8) the spaces
is compact; if in example 8) the spaces  and
and 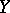 are regarded as Hilbert spaces, then
are regarded as Hilbert spaces, then 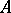 is continuous.
is continuous.
If 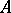 is an operator from
is an operator from 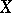 into
into 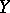 such that
such that 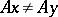 when
when 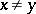 ,
, 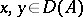 , then the inverse operator
, then the inverse operator 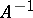 to
to 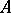 can be defined; the question of the existence of an inverse operator and its properties is related to the theorem of the existence and uniqueness of a solution of the equation
can be defined; the question of the existence of an inverse operator and its properties is related to the theorem of the existence and uniqueness of a solution of the equation 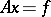 ; if
; if 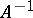 exists, then
exists, then 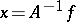 when
when 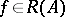 .
.
For operators on a vector space it is possible to define a sum, multiplication by a number and an operator product. If 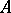 ,
, 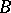 are operators from
are operators from 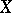 into
into  with domains of definition
with domains of definition 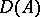 and
and 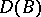 , respectively, then the operator, written as
, respectively, then the operator, written as 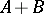 , with domain of definition
, with domain of definition
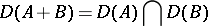 |
and acting according to the rule
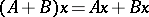 |
if 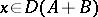 , is called the sum of the operators
, is called the sum of the operators 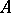 and
and 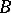 .
.
The operator, written as 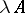 , with domain of definition
, with domain of definition
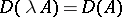 |
and acting according to the rule
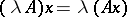 |
if 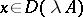 , is called the product of the operator
, is called the product of the operator 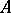 by the number
by the number 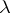 . The operator product is defined as composition of mappings: If
. The operator product is defined as composition of mappings: If 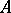 is an operator from
is an operator from 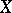 into
into 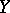 and
and 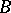 is an operator from
is an operator from  into
into 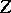 , then the operator
, then the operator 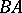 , with domain of definition
, with domain of definition
 |
and acting according to the rule
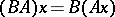 |
if 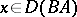 , is called the product of
, is called the product of  and
and 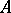 .
.
If 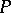 is an everywhere-defined operator on
is an everywhere-defined operator on 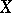 such that
such that  , then
, then 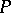 is called a projection operator or projector in
is called a projection operator or projector in 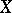 ; if
; if 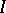 is an everywhere-defined operator on
is an everywhere-defined operator on 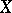 such that
such that 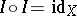 , then
, then 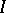 is called an involution in
is called an involution in 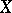 .
.
The theory of operators constitutes the most important part of linear and non-linear functional analysis, being in particular a basic instrument in the theory of dynamical systems, representations of groups and algebras and a most important mathematical instrument in mathematical physics and quantum mechanics.
References
| [1] | L.A. [L.A. Lyusternik] Liusternik, "Elements of functional analysis" , F. Ungar (1961) (Translated from Russian) |
| [2] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [3] | L.V. Kantorovich, G.P. Akilov, "Functional analysis in normed spaces" , Pergamon (1964) (Translated from Russian) |
| [4] | N. Dunford, J.T. Schwartz, "Linear operators" , 1–3 , Interscience (1958) |
| [5] | R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965) |
| [6] | K. Yosida, "Functional analysis" , Springer (1980) |
Comments
References
| [a1] | T. Kato, "Perturbation theory for linear operators" , Springer (1976) |
| [a2] | A.E. Taylor, D.C. Lay, "Introduction to functional analysis" , Wiley (1980) pp. Chapt. 5 |
| [a3] | F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French) |
| [a4] | W. Rudin, "Functional analysis" , McGraw-Hill (1973) |
| [a5] | I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1981) |
Operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Operator&oldid=29264