Continuous operator

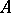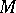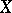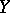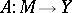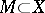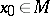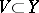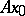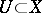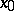A continuous mapping of a subset of a topological space , which as a role is also a vector space, into a space of the same type, specifically: A mapping , , is continuous at a point if for any neighbourhood of the point there is a neighbourhood of such that 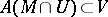; a mapping 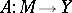is continuous on a set 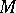if it is continuous at every point of .

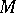For an operator 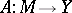to be continuous on 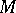it is necessary and sufficient that for every open (closed) set 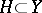the complete inverse image 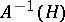is the trace on 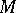of an open (closed) set in 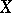, that is, 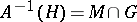, where 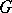is open (closed) in . For continuous operators the chain rule holds: Suppose that , , is continuous on 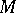(or at 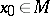) and suppose also that 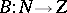, , 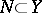is continuous on 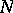(or at 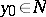). 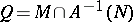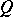If is not empty (or ), then is continuous on (or at ).

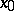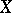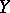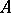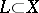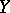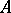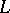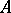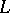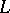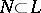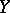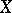When and are topological vector spaces and is a linear continuous operator on a linear subspace with values in , then the continuity of at some point of , say, at the origin, implies the continuity of on the whole of . A continuous operator on a submanifold of a topological vector space is bounded on , that is, the image of any bounded set is bounded in . If and 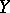are separable, then the compactness of 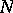implies that of .

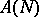An operator 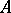is uniformly continuous on 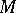if for any neighbourhood of the origin there exists a neighbourhood of the origin 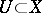such that 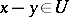implies 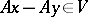. An operator that is linear and continuous on a linear submanifold of a topological vector space is automatically uniformly continuous on this submanifold.

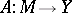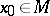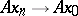Apart from continuity one introduces the concept of countable continuity of an operator. An operator is countably continuous at if for any sequence 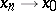, 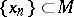. For metrizable spaces continuity and countable continuity coincide.

References

[1]	A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian)
[2]	L.V. Kantorovich, G.P. Akilov, "Functional analysis in normed spaces" , Pergamon (1974) (Translated from Russian)

Comments

In Western literature the term "operatoroperator" tends to be reserved for a mapping between vector spaces. See [a1], [a2].

References

[a1]	N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958)
[a2]	A.E. Taylor, D.C. Lay, "Introduction to functional analysis" , Wiley (1980)