Difference between revisions of "Nevanlinna-Pick problem"
Ulf Rehmann (talk | contribs) m (moved Nevanlinna–Pick problem to Nevanlinna-Pick problem: ascii title) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | n0664801.png | ||
| + | $#A+1 = 35 n = 5 | ||
| + | $#C+1 = 35 : ~/encyclopedia/old_files/data/N066/N.0606480 Nevanlinna\ANDPick problem | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Given a class $ \mathfrak H $ | |
| + | of analytic functions in a domain $ G $ | ||
| + | of the complex plane (or, in a more general context, of a Riemann surface), to find necessary and sufficient conditions for the solvability in $ \mathfrak H $ | ||
| + | of the interpolation problem | ||
| − | + | $$ \tag{1 } | |
| + | f ( z _ \alpha ) = w _ \alpha , | ||
| + | $$ | ||
| − | The | + | where $ \{ z _ \alpha \} $ |
| + | is a subset of $ G $, | ||
| + | $ \{ w _ \alpha \} $ | ||
| + | is some set of complex numbers, and $ \alpha $ | ||
| + | usually runs through a countable (sometimes finite, sometimes even uncountable) index set. The classical result of G. Pick [[#References|[1]]] and R. Nevanlinna [[#References|[2]]] (for finite and countable subsets $ \{ z _ \alpha \} \subset G $, | ||
| + | respectively) yields the solution of this problem, for example, in the class $ B _ {1} $ | ||
| + | of analytic functions in the unit disc that are bounded by 1 in absolute value. The desired condition here is the non-negativity of the quadratic forms | ||
| − | + | $$ | |
| + | \sum _ {j, k = 1 } ^ { n } | ||
| − | + | \frac{1 - w _ {j} \overline{ {w _ {k} }}\; }{1 - z _ {j} \overline{ {z _ {k} }}\; } | |
| − | This result played an important role in describing the structure of the maximal ideal space of the algebra | + | \xi _ {j} \overline{ {\xi _ {k} }}\; ,\ \ |
| + | n \in \mathbf N ,\ \ | ||
| + | \xi _ {j} \in \mathbf C . | ||
| + | $$ | ||
| + | |||
| + | The first proof of this proposition (see [[#References|[3]]], [[#References|[4]]]), as well as quite analogous and similar results for various other function classes $ \mathfrak H $, | ||
| + | relied on algebraic and functional-theoretic methods. Later proofs, based, for example, on reducing the Nevanlinna–Pick problem to a moment problem or obtained from the point of view of the theory of Hilbert spaces, have made it possible to extend the result to uncountable subsets $ \{ z _ \alpha \} \subset G $ | ||
| + | and pointed the way to possible generalizations (see [[#References|[3]]]–[[#References|[5]]]). | ||
| + | |||
| + | A natural development of the Nevanlinna–Pick problem, which necessitated an appeal to functional-analytic methods of investigation, was the question of the solvability of the interpolation problem (1) on a class $ W $ | ||
| + | of right-hand sides $ \{ w _ \alpha \} $; | ||
| + | in this case, as a rule, $ \{ z _ \alpha \} $ | ||
| + | is a countable set (a sequence) of points of $ G $, | ||
| + | while $ W $ | ||
| + | may be one of various spaces of sequences of complex numbers. In connection with the class $ H ^ \infty $ | ||
| + | of bounded analytic functions in the unit disc and the space $ l _ \infty $ | ||
| + | of bounded sequences, a complete description of the corresponding point sequences $ \{ z _ \alpha \} $( | ||
| + | known as universal interpolation sequences) has been obtained (see [[#References|[6]]]) in the form of the condition | ||
| + | |||
| + | $$ \tag{2 } | ||
| + | \prod _ {\begin{array}{c} | ||
| + | j = 1 \\ | ||
| + | j \neq k | ||
| + | \end{array} | ||
| + | } ^ \infty | ||
| + | \left | | ||
| + | \frac{z _ {j} - z _ {k} }{1 - z _ {j} \overline{ {z _ {k} }}\; } | ||
| + | \right | | ||
| + | \geq \delta > 0,\ \ | ||
| + | k \in \mathbf N . | ||
| + | $$ | ||
| + | |||
| + | This result played an important role in describing the structure of the maximal ideal space of the algebra $ H ^ \infty $( | ||
| + | see [[#References|[7]]]) and was at the same time a starting point for extensive research into the Nevanlinna–Pick problem (in the above generalized formulation) for the [[Hardy classes|Hardy classes]] $ H ^ {q} $ | ||
| + | and the spaces $ l _ {p} $( | ||
| + | including weight spaces). It turned out that when $ q = \infty $ | ||
| + | the solution is independent of $ p $ | ||
| + | and is given by condition (2), while when $ q < \infty $ | ||
| + | it necessarily varies when $ q $ | ||
| + | and $ p $ | ||
| + | are changed (see ). Another generalization of the Nevanlinna–Pick problem is connected with the interpolation problem $ \phi _ \alpha ( f ) = w _ \alpha $, | ||
| + | where $ \{ \phi _ \alpha \} $ | ||
| + | is some system of functionals in a class $ \mathfrak H $. | ||
| + | The problem of describing the set $ \{ \{ \phi _ \alpha ( f ) \} : f \in \mathfrak H \} $ | ||
| + | may be regarded as a generalization of the well-known [[Coefficient problem|coefficient problem]] for classes of analytic functions. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> G. Pick, "Ueber die Beschränkungen analytischer Funktionen, welche durch vorgegebene Funktionswerte bewirkt werden" ''Math. Ann.'' , '''77''' (1916) pp. 7–23</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R. Nevanlinna, "Ueber beschränkte analytische Funktionen" ''Ann. Acad. Sci. Fenn. Ser. A'' , '''32''' : 7 (1929) pp. 1–15</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M.G. Krein, A.A. Nudel'man, "The Markov moment problem and extremal problems" , Amer. Math. Soc. (1977) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J.B. Garnett, "Bounded analytic functions" , Acad. Press (1981)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B. Sz.-Nagy, A. Korányi, "Rélations d'un problem de Nevanlinna et Pick avec la théorie des opérateurs de l'espace Hilbertien" ''Acta Math. Acad. Sci. Hung.'' , '''7''' (1956) pp. 295–303</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> L. Carleson, "An interpolation problem for bounded analytic functions" ''Amer. J. Math.'' , '''80''' : 4 (1958) pp. 921–930</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> S.V. Shvedenko, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066480/n06648035.png" />-interpolation sequences in the unit disk" ''Math. USSR Sb.'' , '''46''' : 4 (1983) pp. 473–492 ''Mat. Sb.'' , '''118''' : 4 (1982) pp. 470–489</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G. Pick, "Ueber die Beschränkungen analytischer Funktionen, welche durch vorgegebene Funktionswerte bewirkt werden" ''Math. Ann.'' , '''77''' (1916) pp. 7–23</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R. Nevanlinna, "Ueber beschränkte analytische Funktionen" ''Ann. Acad. Sci. Fenn. Ser. A'' , '''32''' : 7 (1929) pp. 1–15</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M.G. Krein, A.A. Nudel'man, "The Markov moment problem and extremal problems" , Amer. Math. Soc. (1977) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J.B. Garnett, "Bounded analytic functions" , Acad. Press (1981)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B. Sz.-Nagy, A. Korányi, "Rélations d'un problem de Nevanlinna et Pick avec la théorie des opérateurs de l'espace Hilbertien" ''Acta Math. Acad. Sci. Hung.'' , '''7''' (1956) pp. 295–303</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> L. Carleson, "An interpolation problem for bounded analytic functions" ''Amer. J. Math.'' , '''80''' : 4 (1958) pp. 921–930</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> S.V. Shvedenko, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066480/n06648035.png" />-interpolation sequences in the unit disk" ''Math. USSR Sb.'' , '''46''' : 4 (1983) pp. 473–492 ''Mat. Sb.'' , '''118''' : 4 (1982) pp. 470–489</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
This classical topic was reactivated and extended to matrix-valued functions in the 1960s and the beginning of the 1970s. Connections with operator theory became essential in the new developments (see, e.g., [[#References|[a1]]]–[[#References|[a3]]]). Applications to problems in control theory, which appeared in the 1980s, required a revision of the theory and the development of computational methods, in particular, for rational matrix functions (see [[#References|[a4]]], [[#References|[a5]]]). | This classical topic was reactivated and extended to matrix-valued functions in the 1960s and the beginning of the 1970s. Connections with operator theory became essential in the new developments (see, e.g., [[#References|[a1]]]–[[#References|[a3]]]). Applications to problems in control theory, which appeared in the 1980s, required a revision of the theory and the development of computational methods, in particular, for rational matrix functions (see [[#References|[a4]]], [[#References|[a5]]]). | ||
| − | See also [[H^infinity-control-theory| | + | See also [[H^infinity-control-theory| $ H ^ \infty $ |
| + | control theory]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.M. [V.M. Adamyan] Adamjan, D.Z. Arov, M.G. Krein, "Analytic properties of Schmidt pairs for a Hankel operator and the generalized Schur–Tagaki problem" ''Math. USSR Sb.'' , '''15''' (1971) pp. 31–73 ''Mat. Sb.'' , '''86''' : 1 (1971) pp. 34–75</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Rosenblum, J. Rovnyak, "Hardy classes and operator theory" , Oxford Univ. Press (1985)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D. Sarason, "Operator-theoretic aspects of the Nevanlinna–Pick interpolation problem" S.C. Power (ed.) , ''Operators and function theory'' , Reidel (1984) pp. 279–314</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Kimura, "Directional interpolation approach in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066480/n06648037.png" />-optimization" ''IEEE Trans. Autom. Control'' , '''32''' (1987) pp. 1085–1093</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D.J.N. Limebeer, B.D.O. Anderson, "An interpolation theory approach to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066480/n06648038.png" /> controller degree bounds" ''Linear Algebra Appl.'' , '''98''' (1988) pp. 347–386</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J.A. Ball, "Nevanlinna–Pick interpolation: Generalizations and applications" J.B. Conway (ed.) , ''Proc. Asymmetric Algebras and Invariant Subspaces. Conf. Indian Univ.'' , Pitman (To appear)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> H. Dym, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066480/n06648039.png" /> contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , Amer. Math. Soc. (1989)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> J.W. Helton, "Operator theory, analytic functions, matrices, and electrical engineering" , Amer. Math. Soc. (1987)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> P.L. Duren, "Theory of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066480/n06648040.png" /> spaces" , Acad. Press (1970)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> V.M. [V.M. Adamyan] Adamjan, D.Z. Arov, M.G. Krein, "Analytic properties of Schmidt pairs for a Hankel operator and the generalized Schur–Tagaki problem" ''Math. USSR Sb.'' , '''15''' (1971) pp. 31–73 ''Mat. Sb.'' , '''86''' : 1 (1971) pp. 34–75</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Rosenblum, J. Rovnyak, "Hardy classes and operator theory" , Oxford Univ. Press (1985)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D. Sarason, "Operator-theoretic aspects of the Nevanlinna–Pick interpolation problem" S.C. Power (ed.) , ''Operators and function theory'' , Reidel (1984) pp. 279–314</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Kimura, "Directional interpolation approach in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066480/n06648037.png" />-optimization" ''IEEE Trans. Autom. Control'' , '''32''' (1987) pp. 1085–1093</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D.J.N. Limebeer, B.D.O. Anderson, "An interpolation theory approach to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066480/n06648038.png" /> controller degree bounds" ''Linear Algebra Appl.'' , '''98''' (1988) pp. 347–386</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J.A. Ball, "Nevanlinna–Pick interpolation: Generalizations and applications" J.B. Conway (ed.) , ''Proc. Asymmetric Algebras and Invariant Subspaces. Conf. Indian Univ.'' , Pitman (To appear)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> H. Dym, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066480/n06648039.png" /> contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , Amer. Math. Soc. (1989)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> J.W. Helton, "Operator theory, analytic functions, matrices, and electrical engineering" , Amer. Math. Soc. (1987)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> P.L. Duren, "Theory of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066480/n06648040.png" /> spaces" , Acad. Press (1970)</TD></TR></table> | ||
Latest revision as of 08:02, 6 June 2020
Given a class $ \mathfrak H $
of analytic functions in a domain $ G $
of the complex plane (or, in a more general context, of a Riemann surface), to find necessary and sufficient conditions for the solvability in $ \mathfrak H $
of the interpolation problem
$$ \tag{1 } f ( z _ \alpha ) = w _ \alpha , $$
where $ \{ z _ \alpha \} $ is a subset of $ G $, $ \{ w _ \alpha \} $ is some set of complex numbers, and $ \alpha $ usually runs through a countable (sometimes finite, sometimes even uncountable) index set. The classical result of G. Pick [1] and R. Nevanlinna [2] (for finite and countable subsets $ \{ z _ \alpha \} \subset G $, respectively) yields the solution of this problem, for example, in the class $ B _ {1} $ of analytic functions in the unit disc that are bounded by 1 in absolute value. The desired condition here is the non-negativity of the quadratic forms
$$ \sum _ {j, k = 1 } ^ { n } \frac{1 - w _ {j} \overline{ {w _ {k} }}\; }{1 - z _ {j} \overline{ {z _ {k} }}\; } \xi _ {j} \overline{ {\xi _ {k} }}\; ,\ \ n \in \mathbf N ,\ \ \xi _ {j} \in \mathbf C . $$
The first proof of this proposition (see [3], [4]), as well as quite analogous and similar results for various other function classes $ \mathfrak H $, relied on algebraic and functional-theoretic methods. Later proofs, based, for example, on reducing the Nevanlinna–Pick problem to a moment problem or obtained from the point of view of the theory of Hilbert spaces, have made it possible to extend the result to uncountable subsets $ \{ z _ \alpha \} \subset G $ and pointed the way to possible generalizations (see [3]–[5]).
A natural development of the Nevanlinna–Pick problem, which necessitated an appeal to functional-analytic methods of investigation, was the question of the solvability of the interpolation problem (1) on a class $ W $ of right-hand sides $ \{ w _ \alpha \} $; in this case, as a rule, $ \{ z _ \alpha \} $ is a countable set (a sequence) of points of $ G $, while $ W $ may be one of various spaces of sequences of complex numbers. In connection with the class $ H ^ \infty $ of bounded analytic functions in the unit disc and the space $ l _ \infty $ of bounded sequences, a complete description of the corresponding point sequences $ \{ z _ \alpha \} $( known as universal interpolation sequences) has been obtained (see [6]) in the form of the condition
$$ \tag{2 } \prod _ {\begin{array}{c} j = 1 \\ j \neq k \end{array} } ^ \infty \left | \frac{z _ {j} - z _ {k} }{1 - z _ {j} \overline{ {z _ {k} }}\; } \right | \geq \delta > 0,\ \ k \in \mathbf N . $$
This result played an important role in describing the structure of the maximal ideal space of the algebra $ H ^ \infty $( see [7]) and was at the same time a starting point for extensive research into the Nevanlinna–Pick problem (in the above generalized formulation) for the Hardy classes $ H ^ {q} $ and the spaces $ l _ {p} $( including weight spaces). It turned out that when $ q = \infty $ the solution is independent of $ p $ and is given by condition (2), while when $ q < \infty $ it necessarily varies when $ q $ and $ p $ are changed (see ). Another generalization of the Nevanlinna–Pick problem is connected with the interpolation problem $ \phi _ \alpha ( f ) = w _ \alpha $, where $ \{ \phi _ \alpha \} $ is some system of functionals in a class $ \mathfrak H $. The problem of describing the set $ \{ \{ \phi _ \alpha ( f ) \} : f \in \mathfrak H \} $ may be regarded as a generalization of the well-known coefficient problem for classes of analytic functions.
References
| [1] | G. Pick, "Ueber die Beschränkungen analytischer Funktionen, welche durch vorgegebene Funktionswerte bewirkt werden" Math. Ann. , 77 (1916) pp. 7–23 |
| [2] | R. Nevanlinna, "Ueber beschränkte analytische Funktionen" Ann. Acad. Sci. Fenn. Ser. A , 32 : 7 (1929) pp. 1–15 |
| [3] | M.G. Krein, A.A. Nudel'man, "The Markov moment problem and extremal problems" , Amer. Math. Soc. (1977) (Translated from Russian) |
| [4] | J.B. Garnett, "Bounded analytic functions" , Acad. Press (1981) |
| [5] | B. Sz.-Nagy, A. Korányi, "Rélations d'un problem de Nevanlinna et Pick avec la théorie des opérateurs de l'espace Hilbertien" Acta Math. Acad. Sci. Hung. , 7 (1956) pp. 295–303 |
| [6] | L. Carleson, "An interpolation problem for bounded analytic functions" Amer. J. Math. , 80 : 4 (1958) pp. 921–930 |
| [7] | S.V. Shvedenko, "On 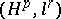 -interpolation sequences in the unit disk" Math. USSR Sb. , 46 : 4 (1983) pp. 473–492 Mat. Sb. , 118 : 4 (1982) pp. 470–489 -interpolation sequences in the unit disk" Math. USSR Sb. , 46 : 4 (1983) pp. 473–492 Mat. Sb. , 118 : 4 (1982) pp. 470–489 |
Comments
This classical topic was reactivated and extended to matrix-valued functions in the 1960s and the beginning of the 1970s. Connections with operator theory became essential in the new developments (see, e.g., [a1]–[a3]). Applications to problems in control theory, which appeared in the 1980s, required a revision of the theory and the development of computational methods, in particular, for rational matrix functions (see [a4], [a5]).
See also $ H ^ \infty $ control theory.
References
| [a1] | V.M. [V.M. Adamyan] Adamjan, D.Z. Arov, M.G. Krein, "Analytic properties of Schmidt pairs for a Hankel operator and the generalized Schur–Tagaki problem" Math. USSR Sb. , 15 (1971) pp. 31–73 Mat. Sb. , 86 : 1 (1971) pp. 34–75 |
| [a2] | M. Rosenblum, J. Rovnyak, "Hardy classes and operator theory" , Oxford Univ. Press (1985) |
| [a3] | D. Sarason, "Operator-theoretic aspects of the Nevanlinna–Pick interpolation problem" S.C. Power (ed.) , Operators and function theory , Reidel (1984) pp. 279–314 |
| [a4] | H. Kimura, "Directional interpolation approach in 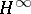 -optimization" IEEE Trans. Autom. Control , 32 (1987) pp. 1085–1093 -optimization" IEEE Trans. Autom. Control , 32 (1987) pp. 1085–1093 |
| [a5] | D.J.N. Limebeer, B.D.O. Anderson, "An interpolation theory approach to 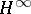 controller degree bounds" Linear Algebra Appl. , 98 (1988) pp. 347–386 controller degree bounds" Linear Algebra Appl. , 98 (1988) pp. 347–386 |
| [a6] | J.A. Ball, "Nevanlinna–Pick interpolation: Generalizations and applications" J.B. Conway (ed.) , Proc. Asymmetric Algebras and Invariant Subspaces. Conf. Indian Univ. , Pitman (To appear) |
| [a7] | H. Dym, "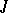 contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , Amer. Math. Soc. (1989) contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , Amer. Math. Soc. (1989) |
| [a8] | J.W. Helton, "Operator theory, analytic functions, matrices, and electrical engineering" , Amer. Math. Soc. (1987) |
| [a9] | P.L. Duren, "Theory of 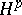 spaces" , Acad. Press (1970) spaces" , Acad. Press (1970) |
Nevanlinna-Pick problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nevanlinna-Pick_problem&oldid=22839