Nevanlinna-Pick problem
Given a class $ \mathfrak H $
of analytic functions in a domain $ G $
of the complex plane (or, in a more general context, of a Riemann surface), to find necessary and sufficient conditions for the solvability in $ \mathfrak H $
of the interpolation problem
$$ \tag{1 } f ( z _ \alpha ) = w _ \alpha , $$
where $ \{ z _ \alpha \} $ is a subset of $ G $, $ \{ w _ \alpha \} $ is some set of complex numbers, and $ \alpha $ usually runs through a countable (sometimes finite, sometimes even uncountable) index set. The classical result of G. Pick [1] and R. Nevanlinna [2] (for finite and countable subsets $ \{ z _ \alpha \} \subset G $, respectively) yields the solution of this problem, for example, in the class $ B _ {1} $ of analytic functions in the unit disc that are bounded by 1 in absolute value. The desired condition here is the non-negativity of the quadratic forms
$$ \sum _ {j, k = 1 } ^ { n } \frac{1 - w _ {j} \overline{ {w _ {k} }}\; }{1 - z _ {j} \overline{ {z _ {k} }}\; } \xi _ {j} \overline{ {\xi _ {k} }}\; ,\ \ n \in \mathbf N ,\ \ \xi _ {j} \in \mathbf C . $$
The first proof of this proposition (see [3], [4]), as well as quite analogous and similar results for various other function classes $ \mathfrak H $, relied on algebraic and functional-theoretic methods. Later proofs, based, for example, on reducing the Nevanlinna–Pick problem to a moment problem or obtained from the point of view of the theory of Hilbert spaces, have made it possible to extend the result to uncountable subsets $ \{ z _ \alpha \} \subset G $ and pointed the way to possible generalizations (see [3]–[5]).
A natural development of the Nevanlinna–Pick problem, which necessitated an appeal to functional-analytic methods of investigation, was the question of the solvability of the interpolation problem (1) on a class $ W $ of right-hand sides $ \{ w _ \alpha \} $; in this case, as a rule, $ \{ z _ \alpha \} $ is a countable set (a sequence) of points of $ G $, while $ W $ may be one of various spaces of sequences of complex numbers. In connection with the class $ H ^ \infty $ of bounded analytic functions in the unit disc and the space $ l _ \infty $ of bounded sequences, a complete description of the corresponding point sequences $ \{ z _ \alpha \} $( known as universal interpolation sequences) has been obtained (see [6]) in the form of the condition
$$ \tag{2 } \prod _ {\begin{array}{c} j = 1 \\ j \neq k \end{array} } ^ \infty \left | \frac{z _ {j} - z _ {k} }{1 - z _ {j} \overline{ {z _ {k} }}\; } \right | \geq \delta > 0,\ \ k \in \mathbf N . $$
This result played an important role in describing the structure of the maximal ideal space of the algebra $ H ^ \infty $( see [7]) and was at the same time a starting point for extensive research into the Nevanlinna–Pick problem (in the above generalized formulation) for the Hardy classes $ H ^ {q} $ and the spaces $ l _ {p} $( including weight spaces). It turned out that when $ q = \infty $ the solution is independent of $ p $ and is given by condition (2), while when $ q < \infty $ it necessarily varies when $ q $ and $ p $ are changed (see ). Another generalization of the Nevanlinna–Pick problem is connected with the interpolation problem $ \phi _ \alpha ( f ) = w _ \alpha $, where $ \{ \phi _ \alpha \} $ is some system of functionals in a class $ \mathfrak H $. The problem of describing the set $ \{ \{ \phi _ \alpha ( f ) \} : f \in \mathfrak H \} $ may be regarded as a generalization of the well-known coefficient problem for classes of analytic functions.
References
| [1] | G. Pick, "Ueber die Beschränkungen analytischer Funktionen, welche durch vorgegebene Funktionswerte bewirkt werden" Math. Ann. , 77 (1916) pp. 7–23 |
| [2] | R. Nevanlinna, "Ueber beschränkte analytische Funktionen" Ann. Acad. Sci. Fenn. Ser. A , 32 : 7 (1929) pp. 1–15 |
| [3] | M.G. Krein, A.A. Nudel'man, "The Markov moment problem and extremal problems" , Amer. Math. Soc. (1977) (Translated from Russian) |
| [4] | J.B. Garnett, "Bounded analytic functions" , Acad. Press (1981) |
| [5] | B. Sz.-Nagy, A. Korányi, "Relations d'un problem de Nevanlinna et Pick avec la théorie des opérateurs de l'espace Hilbertien" Acta Math. Acad. Sci. Hung. , 7 (1956) pp. 295–303 |
| [6] | L. Carleson, "An interpolation problem for bounded analytic functions" Amer. J. Math. , 80 : 4 (1958) pp. 921–930 |
| [7] | S.V. Shvedenko, "On 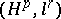 -interpolation sequences in the unit disk" Math. USSR Sb. , 46 : 4 (1983) pp. 473–492 Mat. Sb. , 118 : 4 (1982) pp. 470–489 -interpolation sequences in the unit disk" Math. USSR Sb. , 46 : 4 (1983) pp. 473–492 Mat. Sb. , 118 : 4 (1982) pp. 470–489 |
Comments
This classical topic was reactivated and extended to matrix-valued functions in the 1960s and the beginning of the 1970s. Connections with operator theory became essential in the new developments (see, e.g., [a1]–[a3]). Applications to problems in control theory, which appeared in the 1980s, required a revision of the theory and the development of computational methods, in particular, for rational matrix functions (see [a4], [a5]).
See also $H^\infty$ control theory.
References
| [a1] | V.M. [V.M. Adamyan] Adamjan, D.Z. Arov, M.G. Krein, "Analytic properties of Schmidt pairs for a Hankel operator and the generalized Schur–Tagaki problem" Math. USSR Sb. , 15 (1971) pp. 31–73 Mat. Sb. , 86 : 1 (1971) pp. 34–75 |
| [a2] | M. Rosenblum, J. Rovnyak, "Hardy classes and operator theory" , Oxford Univ. Press (1985) |
| [a3] | D. Sarason, "Operator-theoretic aspects of the Nevanlinna–Pick interpolation problem" S.C. Power (ed.) , Operators and function theory , Reidel (1984) pp. 279–314 |
| [a4] | H. Kimura, "Directional interpolation approach in $H^\infty$-optimization" IEEE Trans. Autom. Control , 32 (1987) pp. 1085–1093 |
| [a5] | D.J.N. Limebeer, B.D.O. Anderson, "An interpolation theory approach to $H^\infty$ controller degree bounds" Linear Algebra Appl. , 98 (1988) pp. 347–386 |
| [a6] | J.A. Ball, "Nevanlinna–Pick interpolation: Generalizations and applications" J.B. Conway (ed.) , Proc. Asymmetric Algebras and Invariant Subspaces. Conf. Indian Univ. , Pitman (To appear) |
| [a7] | H. Dym, "$J$ contractive matrix functions, reproducing kernel Hilbert spaces and interpolation" , Amer. Math. Soc. (1989) |
| [a8] | J.W. Helton, "Operator theory, analytic functions, matrices, and electrical engineering" , Amer. Math. Soc. (1987) |
| [a9] | P.L. Duren, "Theory of $H^p$ spaces" , Acad. Press (1970) |
Nevanlinna–Pick problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nevanlinna%E2%80%93Pick_problem&oldid=22840