Multi-valued mapping
point-to-set mapping
A mapping $ \Gamma : X \rightarrow Y $ associating with each element $ x $ of a set $ X $ a subset $ \Gamma ( x) $ of a set $ Y $. If for each $ x \in X $ the set $ \Gamma ( x) $ consists of one element, then the mapping $ \Gamma $ is called single-valued. A multi-valued mapping $ \Gamma $ can be treated as a single-valued mapping of $ X $ into $ 2 ^ {Y} $, that is, into the set of all subsets of $ Y $.
For two multi-valued mappings $ \Gamma _ {i} : X \rightarrow Y $, $ i = 1 , 2 $, their inclusion is naturally defined: $ \Gamma _ {1} \subset \Gamma _ {2} $ if $ \Gamma _ {1} ( x) \subset \Gamma _ {2} ( x) $ for all $ x \in X $. For any family of multi-valued mappings $ \Gamma _ \alpha : X \rightarrow Y $, $ \alpha \in A $, the union and intersection are defined: $ \Gamma = \cup _ {\alpha \in A } \Gamma _ \alpha $ if $ \Gamma ( x) = \cup _ {\alpha \in A } \Gamma _ \alpha ( x) $ for all $ x \in X $ and $ \Gamma = \cap _ {\alpha \in A } \Gamma _ \alpha $ if $ \Gamma ( x) = \cap _ {\alpha \in A } \Gamma _ \alpha ( x) $ for all $ x \in X $. For any family of multi-valued mappings $ \Gamma _ \alpha : X \rightarrow Y _ \alpha $, $ \alpha \in A $, the multi-valued mapping $ \Gamma = \prod _ {\alpha \in A } \Gamma _ \alpha : X \rightarrow \prod _ {\alpha \in A } Y _ \alpha $ is called the Cartesian product of the multi-valued mappings $ \Gamma _ \alpha $ if $ \Gamma ( x) = \prod _ {\alpha \in A } \Gamma _ \alpha ( x) $. A section of a multi-valued mapping $ \Gamma $ is a single-valued mapping $ f : X \rightarrow Y $ such that $ f ( x) \in \Gamma ( x) $ for all $ x \in X $. The graph of a multi-valued mapping $ \Gamma $ is the set $ G ( \Gamma ) = \{ {( x , y ) \in X \times Y } : {y \in \Gamma ( x) } \} $.
A multi-valued mapping $ \Gamma $ of a topological space $ X $ into a topological space $ Y $ is called upper semi-continuous if for every open set $ U \subset Y $ the set $ \Gamma ^ {+} ( u) = \{ {x \in X } : {\Gamma ( x) \subset U, \Gamma ( x) \neq \emptyset } \} $ is open in $ X $, or equivalently: For any $ x \in X $ and any neighbourhood $ U $ of $ \Gamma ( x) $ there is a neighbourhood $ O x $ of $ x $ such that $ \Gamma ( Ox) \subset U $, where $ \Gamma ( Ox ) = \cup \{ {\Gamma ( y) } : {y \in Ox } \} $. A multi-valued mapping from a topological space $ X $ to a topological space $ Y $ is called lower semi-continuous if for any open set $ U \subset Y $ the set $ \Gamma ^ {-} ( U) = \{ {x \in X } : {\Gamma ( x) \cap U \neq \emptyset } \} $ is open in $ X $. If a multi-valued mapping satisfies both properties simultaneously, then it is called a continuous multi-valued mapping.
Let $ Y $ be a topological vector space. A multi-valued mapping $ \Gamma : X\rightarrow Y $ is called convex-compact valued if $ \Gamma ( x) $ is a convex compact set for all $ x \in X $. For a finite set of multi-valued mappings $ \Gamma _ {i} : X \rightarrow Y $, $ i \in I $, the algebraic sum $ \Gamma = \sum _ {i \in I } \Gamma _ {i} $ is defined by $ \Gamma ( x) = \sum _ {i \in I } \Gamma _ {i} ( x) $. The intersection of any (finite) family of upper semi-continuous (respectively, continuous) multi-valued mappings is upper semi-continuous (respectively, continuous). The Cartesian product of a finite family of upper semi-continuous multi-valued mappings is upper semi-continuous. The algebraic sum of a finite family of upper semi-continuous (convex-compact valued) mappings is upper semi-continuous (convex-compact valued). The intersection and Cartesian product of any family of convex-compact valued mappings is convex-compact valued.
Let $ X $ be a paracompact space and $ Y $ a locally convex metric linear space (cf. Locally convex space; Linear space; Metric space). Let $ \Gamma : X \rightarrow Y $ be a multi-valued mapping which is upper semi-continuous and is such that $ \Gamma ( x) $ is closed in $ Y $ for every $ x \in X $. Then the multi-valued mapping $ \Gamma $ admits continuous sections. Let $ ( X , \mathfrak A ) $ and $ ( Y , \mathfrak B ) $ be spaces with given $ \sigma $- algebras $ \mathfrak A $ and $ \mathfrak B $; a multi-valued mapping $ \Gamma : ( X , \mathfrak A ) \rightarrow ( Y , \mathfrak B ) $ is called measurable if the graph $ G ( \Gamma ) $ belongs to the smallest $ \sigma $- algebra $ \mathfrak A \times \mathfrak B $ of $ X \times Y $ containing all sets of the form $ A \times B $, where $ A \in \mathfrak A $ and $ B \in \mathfrak B $. If $ \Gamma $ is a measurable multi-valued mapping from $ ( X , \mathfrak A ) $ to a complete separable metric space $ ( Y , \mathfrak B ) $, where $ \mathfrak B $ is the Borel $ \sigma $- algebra of $ Y $, then $ \Gamma $ has measurable sections $ f $.
References
| [1] | K. Kuratowski, "Topology" , 1–2 , Acad. Press (1966–1968) (Translated from French) |
Comments
A multi-valued mapping is also called a set-valued or many-valued mapping. Sections are also called selections.
Theorems which prove that certain kinds of multi-valued mappings admit selections are called selection theorems. The measurable selection theorem stated in the last sentence of the main article above is known as von Neumann's measurable choice theorem. A number of selection theorems and some applications are discussed in [a4].
References
| [a1] | E. Michael, "Continuous selections" Ann. of Math. , 63 (1956) pp. 361–382 |
| [a2] | E.A. Michael, "A survey of continuous selections" W.M. Fleischmann (ed.) , Set valued mappings, selections and topological properties of 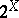 (Proc. Conf. SUNY Buffalo, 1969) , Lect. notes in math. , 171 , Springer (1970) pp. 54–58 (Proc. Conf. SUNY Buffalo, 1969) , Lect. notes in math. , 171 , Springer (1970) pp. 54–58 |
| [a3] | K. Przeslawski, D. Yost, "Continuity properties of selectors and Michael's Theorem" Mich. Math. J. , 36 (1989) pp. 113–134 |
| [a4] | T. Parthasarathy, "Selection theorems and their applications" , Lect. notes in math. , 263 , Springer (1972) |
Multi-valued mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multi-valued_mapping&oldid=47923