Modulus
A numerical characteristic of various mathematical objects. Usually the value of a modulus is a non-negative real number, an element of 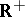 , having certain characteristic properties, conditioned by properties of the set
, having certain characteristic properties, conditioned by properties of the set  of objects under discussion. The notion of a modulus figures in various branches of mathematics, although sometimes under other names — absolute value; norm, etc. All of them, in essence, are generalizations of the idea of the absolute value of a real or complex number (but the term modulus usually means a generalization of special form). Here the function
of objects under discussion. The notion of a modulus figures in various branches of mathematics, although sometimes under other names — absolute value; norm, etc. All of them, in essence, are generalizations of the idea of the absolute value of a real or complex number (but the term modulus usually means a generalization of special form). Here the function 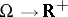 turns out to be a morphism of some structure in
turns out to be a morphism of some structure in  onto one of the (algebraic) structures in
onto one of the (algebraic) structures in 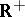 , among which the most important ones are the order, the addition and the multiplication. In this connection the basic properties of the absolute value must be preserved (see below:
, among which the most important ones are the order, the addition and the multiplication. In this connection the basic properties of the absolute value must be preserved (see below: 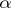 )–
)– )). In more abstract situations it is natural to use an ordered semi-ring instead of
)). In more abstract situations it is natural to use an ordered semi-ring instead of 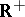 (this conception of a modulus is satisfied by, for example, a measure, a capacity, a mass, etc.). Finally, the term modulus denotes numerical characteristics of other objects, such as, for example, the moduli of a plane domain, the modulus of an annulus, the moduli of a Riemann surface, and the modulus of continuity or smoothness (cf. Continuity, modulus of; Smoothness, modulus of) (and even moduli in the theory of elasticity (compression, shear)). However, in all these cases it is possible to introduce a value functionally depending on the modulus and more adequately reflecting the nature of the objects under discussion (for example, for a family of curves, the extremal length instead of the modulus).
(this conception of a modulus is satisfied by, for example, a measure, a capacity, a mass, etc.). Finally, the term modulus denotes numerical characteristics of other objects, such as, for example, the moduli of a plane domain, the modulus of an annulus, the moduli of a Riemann surface, and the modulus of continuity or smoothness (cf. Continuity, modulus of; Smoothness, modulus of) (and even moduli in the theory of elasticity (compression, shear)). However, in all these cases it is possible to introduce a value functionally depending on the modulus and more adequately reflecting the nature of the objects under discussion (for example, for a family of curves, the extremal length instead of the modulus).
Examples. 1) The modulus of an element  of a semi-ordered space
of a semi-ordered space 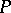 is the number
is the number
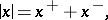 |
where 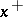 (
(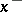 ) is the positive (negative) part of
) is the positive (negative) part of  . Here, as for real numbers,
. Here, as for real numbers,
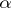 )
)  ;
; 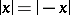 ;
;
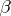 )
) 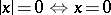 (0 is the zero in
(0 is the zero in 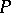 ).
).
2) The modulus of an element  of a separable pre-Hilbert space
of a separable pre-Hilbert space 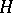 , in particular, a finite-dimensional vector space, is the number
, in particular, a finite-dimensional vector space, is the number
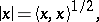 |
where 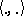 is the inner product in
is the inner product in 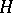 . This is a norm in
. This is a norm in 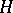 and thus
and thus
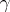 )
) 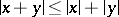 ;
;
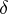 )
) 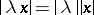 ,
, 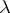 a scalar.
a scalar.
3) The modulus of an element  of a locally compact skew-field is the number
of a locally compact skew-field is the number
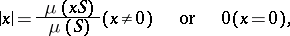 |
where 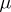 is a Haar measure on the additive group of
is a Haar measure on the additive group of 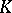 and
and 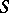 is a measurable subset. Here, as for numbers from
is a measurable subset. Here, as for numbers from 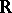 ,
, 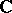 ,
,  ,
,
 )
) 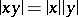 .
.
A generalization of this idea is the modulus of an automorphism.
4) The modulus of an endomorphism 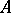 of a vector space
of a vector space 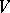 over a field
over a field 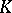 (a special case is the modulus of an automorphism) is the number
(a special case is the modulus of an automorphism) is the number 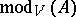 , which turns out to be simply equal to
, which turns out to be simply equal to 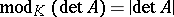 , where
, where  is the modulus of Example 3).
is the modulus of Example 3).
Comments
Often a modulus is simply some numerical parameter on which the mathematical object under consideration depends. For instance, the modulus of an elliptic integral, the complementary modulus (in Jacobi elliptic functions) or the modulus of a congruence. Cf. also Norm on a field; Valuation.
Modulus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Modulus&oldid=16003