Mean-value characterization
Harmonic functions.
Let $S ( x , r )$ denote the sphere of radius $r$ and centre $x$ in ${\bf R} ^ { n }$ and let $d \sigma _ { r }$ be the normalized Lebesgue measure on $S ( x , r )$. One version of the classical converse of Gauss' mean-value theorem for harmonic functions asserts that a function $f \in C ( R ^ { n } )$ which satisfies
\begin{equation} \tag{a1} \int _ { S ( x , r ) } f ( y ) d \sigma _ { r } ( y ) = f ( x ) , x \in \mathbf{R} ^ { n } , r \in \mathbf{R} ^ { + }, \end{equation}
is harmonic in ${\bf R} ^ { n }$ (cf. also Harmonic function). In fact, one need only require that (a1) holds for $0 < r < \rho ( x )$, where $\rho$ is an arbitrary positive function of $x$. A corresponding "local" result holds for continuous functions defined on an arbitrary domain in ${\bf R} ^ { n }$.
Remarkably, for the harmonicity of $f$ it suffices that (a1) holds only for two distinct values of $r$ (and all $x$), so long as the radii are not related in a special way. Specifically, let
\begin{equation*} j _ { n } ( \zeta ) = \Gamma \left( \frac { n } { 2 } \right) \left( \frac { 2 } { \zeta } \right) ^ { ( n - 2 ) / 2 } J _ { ( n - 2 ) / 2 } ( \zeta ), \end{equation*}
where $J _ { k }$ is the Bessel function of the first kind of order $k$ (cf. also Bessel functions), and let $H _ { n }$ be the set of positive quotients of zeros of $j _ { n } ( \zeta ) - 1$. J. Delsarte proved that if (a1) holds for $r = r _{1}$ and $r = r_2$ and $r _ { 1 } / r _ { 2 } \notin H _ { n}$, then $f$ is harmonic in ${\bf R} ^ { n }$ [a11], cf. [a20]. (In fact, $H _ { 3 } = \{ 1 \}$, so any two distinct radii are sufficient in dimension $3$.) In [a10], Delsarte's theorem is extended to non-compact irreducible symmetric spaces of rank $1$. There is also a local version of this result [a9], [a21]. Let $B _ { R }$ be the ball of radius $R$ centred at $0$ in ${\bf R} ^ { n }$. Now, if $f \in C ( B _ { R } )$ satisfies (a1) for $r = r _ { 1 } , r _ { 2 }$ ($r _ { 1 } / r _ { 2 } \notin H _ { n}$) and $x$ such that $| x | + r_j < R$, then $f$ is harmonic on $B _ { R }$ so long as $r _ { 1 } + r _ { 2 } < R$.
In this connection, one should also mention Littlewood's one-circle problem, solved by W. Hansen and N. Nadirashvili [a14]. Let $f$ be a bounded continuous function on the open unit disc $U$ in $\mathbf{R} ^ { 2 }$. Suppose that for each point in $U$ there exists an $r = r ( x )$ such that the mean-value condition of (a1) holds. Must $f$ be harmonic? The answer turns out to be "no" [a14]. On the other hand, the one-radius condition obtained by replacing the peripheral mean in (a1) by the (areal) average over the disc of radius $r ( x )$ does imply harmonicity [a13]. This last result extends to functions defined on arbitrary bounded domains in ${\bf R} ^ { n }$ (and many unbounded domains as well); one can also weaken the boundedness assumption on $f$ to $| f | < h$ for some positive harmonic function $h$. For a survey of these and related results, see [a12].
Interesting new phenomena arise when one allows the integration to extend over the full space on which $f$ is defined. Consider, for instance, functions integrable with respect to the (normalized) Lebesgue measure $m$ on the unit ball $B$ in $\mathbf{C} ^ { n }$. If $f$ is harmonic with respect to the invariant Laplacian [a17], 4.1, then
\begin{equation*} \int _ { B } ( f \circ \psi ) d m = f ( \psi ( 0 ) ) \end{equation*}
for every $\psi$ in $\operatorname{Aut}( B )$. The converse holds if and only if $n < 12$ [a1], cf. [a7] and, for a Euclidean analogue, [a6]. Asymptotic mean-value conditions for (non-integrable) functions on ${\bf R} ^ { n }$ are studied in [a8]. Finally, for a detailed overview of the whole subject, see [a15].
Generalization.
The extent to which mean-value theorems and their converses generalize to differential equations other than $\Delta u = 0$ is explored in [a22]. There it is shown that if $P ( \xi _ { 1 } , \dots , \xi _ { n } )$ is a homogeneous polynomial, then $u \in C ( \mathbf{R} ^ { n } )$ is a (weak) solution of the differential equation $P ( D ) u = 0$ if and only if it satisfies the generalized mean-value condition
\begin{equation} \tag{a2} \int u ( x + r t ) d \mu ( t ) = 0 , \quad x \in \mathbf{R} ^ { n } , r \in \mathbf{R} ^ { + }, \end{equation}
where $\mu$ is an appropriate complex measure supported on the unit ball of ${\bf R} ^ { n }$ and $D = ( \partial / \partial x _ { 1 } , \dots , \partial / \partial x _ { n } )$. (The choice $d \mu = d \sigma _ { 1 } - \delta _ { 0 }$ corresponds to (a1).) The local version of this result requires that (a2) holds for all $x \in \mathcal{D} \subset \mathbf{R} ^ { n }$ and all $0 < r < \text { dist } ( x , \partial \cal D )$. Solutions of $P ( D ) u = 0$ are also characterized by two-radius theorems of Delsarte type [a22], [a23], cf. [a19].
Pluriharmonic and separately harmonic functions.
Mean-value characterizations of pluriharmonic functions (i.e., real parts of holomorphic functions, cf. also Pluriharmonic function) and separately harmonic functions (i.e., functions harmonic with respect to each variable $z_j$, $1 \leq j \leq n$) are studied in [a3]. Let
\begin{equation*} \nu ( \zeta - a ) = \frac { 1 } { ( 2 \pi i ) ^ { n } } \sum _ { k = 1 } ^ { n } ( - 1 ) ^ { k - 1 } ( \overline { \zeta } _ { k } - \overline { a } _ { k } ) d \overline { \zeta } [ k ] \bigwedge d \zeta; \end{equation*}
here $d \overline { \zeta } [ k ] = d \overline { \zeta } _ { 1 } \wedge \ldots \wedge d \overline { \zeta } _ { k - 1 } \wedge d \overline { \zeta }_{ k + 1} \wedge \ldots \wedge d \overline { \zeta }_{n}$, $d \zeta = d \zeta _ { 1 } \wedge \ldots \wedge d \zeta _ { n }$. If $\mathcal{D} \subset \mathbf{C} ^ { n }$ is a complete bounded Reinhardt domain with centre at the point $a$ and $f$ is separately harmonic in $\mathcal{D}$ and continuous in $\overline{\mathcal{D}}$, then
\begin{equation} \tag{a3} \frac { \pi ^ { n } } { n \operatorname { vol } ( {\cal D} ) } \int _ { \partial \cal D } f ( \zeta ) \nu ( \zeta - a ) = f ( a ). \end{equation}
Take for $\mathcal{D}$ the $n$-circular ellipsoids with centre at the point $a$,
\begin{equation*} \mathcal{D} _ { j , k } ( a ) = \{ z : b _ { j } ^ { 1 } | z _ { 1 } - a _ { 1 } | ^ { 2 } + \ldots + b _ { j } ^ { n } | z _ { n } - a _ { n } | ^ { 2 } < r _ { j , k } ^ { 2 } \}, \end{equation*}
where $k = 1,2$, $j = 1 , \ldots , n$, and all $b _ { j } ^ { l } > 0$. Then the following result holds. Let $f \in C ( \mathbf{C} ^ { n } )$ be such that for each $a \in \mathbf{C} ^ {n }$ the $2 n$ conditions obtained by setting in (a3) $\mathcal{D} = \mathcal{D} _ { j , k } ( a )$, $j = 1 , \ldots , n$, and $k = 1,2$ hold. If no $r_{j,1} / r_{j,2} $ belongs to $H _ { 2n }$ and if
\begin{equation*} \operatorname { det } \left\| \frac { 1 } { b _ { j } ^ { l } } \right\| \neq 0, \end{equation*}
then $f$ is separately harmonic in $\mathbf{C} ^ { n }$.
Similarly, if $\mathcal{D} _ { 1 } \subset \mathbf{C} ^ { n }$ is a complete bounded circular (Cartan) domain with centre at the point $a$ (cf. also Reinhardt domain) and $f$ is pluriharmonic in $\mathcal{D} _ { 1 }$ and continuous in $\overline { \mathcal{D} } _ { 1 }$, then
\begin{equation} \tag{a4} \frac { \pi ^ { n } } { n \operatorname { vol } ( \mathcal{D} _ { 1 } ) } \int _ { \partial \mathcal{D} _ { 1 } } f ( \zeta ) \nu ( \zeta - a ) = f ( a ). \end{equation}
Consider now circular ellipsoids with centre at the point $a$:
\begin{equation*} {\cal D} _ { j , k } ^ { p } ( a ) = \end{equation*}
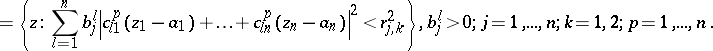 |
Let $\| d _ { lm } ^ { p } \|$ ($l , m = 1 , \dots , n$) be the inverse matrix of 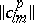 for $p$ fixed. Let $Q = \| q _ { p s , i l} \|$ ($p , s = 1 , \dots , n$; $i , l = 1 , \dots , n$) be the $( n ^ { 2 } \times n ^ { 2 } )$-matrix with entries
for $p$ fixed. Let $Q = \| q _ { p s , i l} \|$ ($p , s = 1 , \dots , n$; $i , l = 1 , \dots , n$) be the $( n ^ { 2 } \times n ^ { 2 } )$-matrix with entries
\begin{equation*} q _ { p s , i l } = d _ { t s } ^ { p } \overline { d } _ { l s } ^ { p }. \end{equation*}
Then the following result holds. Let $f \in C ( \mathbf{C} ^ { n } )$ be such that for every $a \in \mathbf{C} ^ {n }$ the conditions (a4) hold for $\mathcal{D} _ { 1 } = \mathcal{D} _ { j , k } ^ { p } ( a )$, $j = 1 , \ldots , n$, $k = 1,2$, $p = 1 , \dots , n$ ($2 n ^ { 2 }$ conditions). If $r _ { j , 1 }$ and $r_{ j , 2}$ are such that no $r_{j,1} / r_{j,2} $ belongs to $H _ { 2n }$, $\operatorname { det } \| 1 / b _ { j } ^ { l } \| \neq 0$ and $\det Q \neq 0$, then $f$ is pluriharmonic.
Local versions of the above-mentioned results are given also in [a3], as well as mean-value characterizations of pluriharmonic functions and separately harmonic functions by integration over the distinguished boundaries of poly-discs.
Holomorphic and pluriharmonic functions.
In certain situations, Temlyakov–Opial–Siciak-type mean-value theorems (see [a2], [a16], [a18]) can be used to characterize holomorphic and pluriharmonic functions. For $( n - 1 )$-times continuously differentiable functions $f$ on $\mathbf{C} ^ { n }$, the integral representation under discussion can be written as
\begin{equation} \tag{a5} f ( z ) = ( L f ) ( z ) = ( L _ { F_n } f ) ( z ) = \end{equation}
\begin{equation*} = ( 2 \pi i ) ^ { 1 - n } \int _ { \Delta _ { n } } d t \int _ { S } ( F _ { n }\, f ) \times \times \left( ( 1 - t _ { 2 } - \ldots - t _ { n } ) ( z , \zeta ) , \frac { t _ { 2 } } { \zeta _ { 2 } } ( z , \zeta ) , \ldots , \frac { t _ { n } } { \zeta _ { n } } ( z , \zeta ) \right) \frac { d \zeta } { \zeta }, \end{equation*}
where $\Delta _ { n } = \{ ( t _ { 2 } , \dots , t _ { n } ) : t _ { 2 } , \dots , t _ { n } \geq 0 , t _ { 2 } + \dots + t _ { n } \leq 1 \}$ is the unit simplex in the real Euclidean $( n - 1 )$-dimensional space, $S = \{ \zeta : | \zeta _ { j } | = 1 ,\; j = 2 , \dots , n \}$, $z = ( z _ { 1 } , \dots , z _ { n } ) \in \mathbf{C} ^ { n }$, $\zeta = ( 1 , \zeta _ { 2 } , \dots , \zeta _ { n } )$, $d t = d t _ { 2 } \wedge \ldots \wedge d t _ { n }$, $d \zeta / \zeta = d \zeta _ { 2 } / \zeta _ { 2 } \wedge \ldots \wedge d \zeta _ { n } / \zeta _ { n }$, and $( z , \zeta ) = z _ { 1 } + z _ { 2 } \zeta _ { 2 } + \ldots + z _ { n } \zeta _ { n }$. Let $F _ { n }$ denote a certain differential operator of order $n - 1$, which will be specified separately for holomorphic functions, for pluriharmonic functions, and also for anti-holomorphic functions (that is, functions holomorphic with respect to $\overline{z} = ( \overline{z}_{1} , \dots , \overline{z}_ { n } )$). More precisely,
\begin{equation*} F _ { n } f = \left[ \prod _ { j = 1 } ^ { n - 1 } ( F + j ) \right] f, \end{equation*}
with the first-order differential operator to be specified, as mentioned above.
In [a4], the following criteria are proved for functions that are $( n - 1 )$-times continuously differentiable on $\mathbf{C} ^ { n }$.
A function $f$ is holomorphic in $\mathbf{C} ^ { n }$ if and only if (a5) holds with
\begin{equation*} ( F f ) ( z ) = \sum _ { j = 1 } ^ { n } z_j \frac { \partial f ( z ) } { \partial z _ { j } }. \end{equation*}
A function $f$ is anti-holomorphic on $\mathbf{C} ^ { n }$ if and only if (a5) holds with
\begin{equation*} ( F f ) ( z ) = \sum _ { j = 1 } ^ { n } \bar{z}_j \frac { \partial f ( z ) } { \partial \bar{z} _ { j } }. \end{equation*}
A function $f$ is pluriharmonic on $\mathbf{C} ^ { n }$ if and only if (a5) holds with
\begin{equation*} ( F f ) ( z ) = \sum _ { j = 1 } ^ { n } \left( z _ { j } \frac { \partial f ( z ) } { \partial z _ { j } } + \bar{z} _ { j } \frac { \partial f ( z ) } { \partial \bar{z} _ { j } } \right). \end{equation*}
These results remain true without the assumption of smoothness; in this case, derivatives being understood in the distributional sense [a5].
References
| [a1] | P. Ahern, M. Flores, W. Rudin, "An invariant volume-mean-value property" J. Funct. Anal. , 11 (1993) pp. 380–397 |
| [a2] | L.A. Aizenberg, "Pluriharmonic functions" Dokl. Akad. Nauk. SSSR , 124 (1959) pp. 967–969 (In Russian) |
| [a3] | L.A. Aizenberg, C.A. Berenstein, L. Wertheim, "Mean-value characterization of pluriharmonic and separately harmonic functions" Pacific J. Math. , 175 (1996) pp. 295–306 |
| [a4] | L. Aizenberg, E. Liflyand, "Mean-value characterization of holomorphic and pluriharmonic functions" Complex Variables , 32 (1997) pp. 131–146 |
| [a5] | L. Aizenberg, E. Liflyand, "Mean-value characterization of holomorphic and pluriharmonic functions, II" Complex Variables , 39 (1999) pp. 381–390 |
| [a6] | Y. Ben Natan, Y. Weit, "Integrable harmonic functions on ${\bf R} ^ { n }$" J. Funct. Anal. , 150 (1997) pp. 471–477 |
| [a7] | Y. Ben Natan, Y. Weit, "Integrable harmonic functions and symmetric spaces of rank one" J. Funct. Anal. , 160 (1998) pp. 141–149 |
| [a8] | Y. Benyamini, Y. Weit, "Functions satisfying the mean value property in the limit" J. Anal. Math. , 52 (1989) pp. 167–198 |
| [a9] | C.A. Berenstein, R. Gay, "A local version of the two-circles theorem" Israel J. Math. , 55 (1986) pp. 267–288 |
| [a10] | C.A. Berenstein, L. Zalcman, "Pompeiu's problem on symmetric spaces" Comment. Math. Helv. , 55 (1980) pp. 593–621 |
| [a11] | J. Delsarte, "Lectures on topics in mean periodic functions and the two-radius theorem" , Tata Institute, Bombay (1961) |
| [a12] | W. Hansen, "Restricted mean value property and harmonic functions" J. Kral (ed.) et al. (ed.) , Potential Theory–ICPT 94 (Proc. Intern. Conf., Konty) , de Gruyter (1996) pp. 67–90 |
| [a13] | W. Hansen, N. Nadirashvili, "A converse to the mean value theorem for harmonic functions" Acta Math. , 171 (1993) pp. 139–163 |
| [a14] | W. Hansen, N. Nadirashvili, "Littlewood's one circle problem" J. London Math. Soc. , 50 (1994) pp. 349–360 |
| [a15] | I. Netuka, J. Vesely, "Mean value property and harmonic functions" K. GowriSankaran (ed.) et al. (ed.) , Classical and Modern Potential Theory and Applications , Kluwer Acad. Publ. (1994) pp. 359–398 |
| [a16] | Z. Opial, J. Siciak, "Integral formulas for function holomorphic in convex $n$ circular domains" Zeszyty Nauk. Uniw. Jagiello. Prace Mat. , 9 (1963) pp. 67–75 |
| [a17] | W. Rudin, "Function theory in the unit ball of $\mathbf{C} ^ { n }$" , Springer (1980) |
| [a18] | A.A. Temlyakov, "Integral representation of functions of two complex variables" Izv. Akad. Nauk. SSSR Ser. Mat. , 21 (1957) pp. 89–92 (In Russian) |
| [a19] | V.V. Volchkov, "New theorems on the mean for solutions of the Helmholtz equation" Russian Acad. Sci. Sb. Math. , 79 (1994) pp. 281–286 |
| [a20] | V.V. Volchkov, "New two-radii theorems in the theory of harmonic functions" Russian Acad. Sci. Izv. Math. , 44 (1995) pp. 181–192 |
| [a21] | V.V. Volchkov, "The final version of the mean value theorem for harmonic functions" Math. Notes , 59 (1996) pp. 247–252 |
| [a22] | L. Zalcman, "Offbeat integral geometry" Amer. Math. Monthly , 87 (1980) pp. 161–175 |
| [a23] | L. Zalcman, "Mean values and differential equations" Israel J. Math. , 14 (1973) pp. 339–352 |
Mean-value characterization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mean-value_characterization&oldid=55359