Local-global principles for the ring of algebraic integers
Consider the field 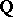 of rational numbers and the ring
of rational numbers and the ring 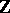 of rational integers. Let
of rational integers. Let 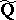 be the field of all algebraic numbers (cf. also Algebraic number) and let
be the field of all algebraic numbers (cf. also Algebraic number) and let 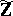 be the ring of all algebraic integers. Then
be the ring of all algebraic integers. Then 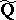 is the algebraic closure of
is the algebraic closure of 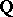 and
and 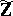 is the integral closure of
is the integral closure of 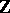 in
in 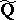 (cf. also Extension of a field). If
(cf. also Extension of a field). If 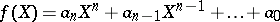 is a polynomial in
is a polynomial in 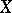 with coefficients in
with coefficients in 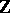 and there exists an
and there exists an 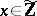 such that
such that 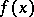 is a unit of
is a unit of 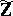 , then the greatest common divisor of
, then the greatest common divisor of  is
is 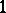 . In 1934, T. Skolem [a14] proved that the converse is also true (Skolem's theorem): Let
. In 1934, T. Skolem [a14] proved that the converse is also true (Skolem's theorem): Let 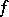 be a primitive polynomial with coefficients in
be a primitive polynomial with coefficients in 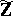 . Then there exists an
. Then there exists an 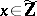 such that
such that 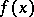 is a unit of
is a unit of 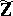 .
.
Here, 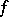 is said to be primitive if the ideal of
is said to be primitive if the ideal of 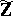 generated by its coefficients is the whole ring.
generated by its coefficients is the whole ring.
E.C. Dade [a2] rediscovered this theorem in 1963. D.R. Estes and R.M. Guralnick [a5] reproved it in 1982 and drew some consequences about local-global principles for modules over 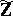 . In 1984, D.C. Cantor and P. Roquette [a1] considered rational functions
. In 1984, D.C. Cantor and P. Roquette [a1] considered rational functions 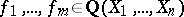 and proved a local-global principle for the "Skolem problem with data f1…fm" (the Cantor–Roquette theorem): Suppose that for each prime number
and proved a local-global principle for the "Skolem problem with data f1…fm" (the Cantor–Roquette theorem): Suppose that for each prime number 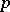 there exists an
there exists an 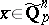 such that
such that 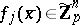 ,
, 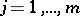 . Then there exists an
. Then there exists an 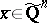 such that
such that 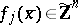 ,
, 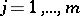 .
.
Here, writing 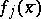 includes the assumption that
includes the assumption that 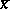 is not a zero of the denominator of
is not a zero of the denominator of 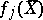 . Also,
. Also, 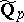 is the algebraic closure of the field
is the algebraic closure of the field 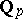 of
of 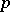 -adic numbers and
-adic numbers and 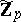 is its valuation ring (cf. also
is its valuation ring (cf. also 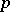 -adic number).
-adic number).
Skolem's theorem follows from the Cantor–Roquette theorem applied to the data 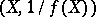 by checking the local condition for each
by checking the local condition for each 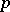 .
.
One may consider the unirational variety 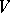 generated in
generated in 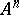 over
over 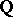 by the
by the 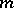 -tuple
-tuple 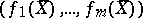 . If
. If 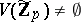 for each
for each 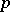 , then, by the Cantor–Roquette theorem,
, then, by the Cantor–Roquette theorem, 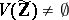 . Rumely's local-global principle [a12], Thm. 1, extends this result to arbitrary varieties: Let
. Rumely's local-global principle [a12], Thm. 1, extends this result to arbitrary varieties: Let 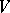 be an absolutely irreducible affine variety over
be an absolutely irreducible affine variety over 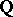 . If
. If 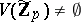 for all prime numbers
for all prime numbers 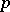 , then
, then 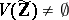 .
.
R. Rumely has enhanced his local-global principle by a density theorem: Let 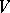 be an affine absolutely irreducible variety over
be an affine absolutely irreducible variety over 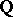 and let
and let 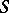 be a finite set of prime numbers. Suppose that for each
be a finite set of prime numbers. Suppose that for each 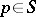 ,
, 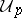 is a non-empty open subset of
is a non-empty open subset of 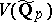 in the
in the 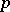 -adic topology, which is stable under the action of the Galois group
-adic topology, which is stable under the action of the Galois group 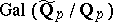 . In addition, assume that
. In addition, assume that 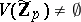 for all
for all 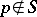 . Then there exists an
. Then there exists an 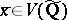 such that for each
such that for each 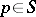 , all conjugates of
, all conjugates of 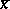 over
over 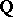 belong to
belong to 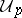 , and for each
, and for each 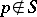 ,
, 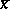 is
is 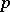 -integral.
-integral.
The proof of this theorem uses complex-analytical methods, especially the Fekete–Szegö theorem from capacity theory. The latter is proved in [a13]. See [a9] for an algebraic proof of the local-global principle using the language of schemes; see [a7] for still another algebraic proof of it, written in the language of classical algebraic geometry. Both proofs enhance the theorem in various ways, see also Local-global principles for large rings of algebraic integers.
As a matter of fact, all these theorems can be proved for an arbitrary number field 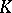 instead of
instead of 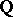 . One has to replace
. One has to replace 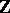 by the ring of integers
by the ring of integers 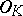 of
of 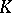 and the prime numbers by the non-zero prime ideals of
and the prime numbers by the non-zero prime ideals of 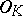 . This is important for the positive solution of Hilbert's tenth problem for
. This is important for the positive solution of Hilbert's tenth problem for 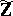 [a12], Thm. 2: There is a primitive recursive procedure to decide whether given polynomials
[a12], Thm. 2: There is a primitive recursive procedure to decide whether given polynomials 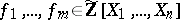 have a common zero in
have a common zero in 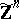 .
.
To this end, recall that the original Hilbert tenth problem for 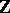 has a negative solution [a8] (cf. also Hilbert problems). Similarly, the local-global principle over
has a negative solution [a8] (cf. also Hilbert problems). Similarly, the local-global principle over 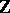 holds only in very few cases, such as quadratic forms.
holds only in very few cases, such as quadratic forms.
In the language of model theory (cf. also Model theory of valued fields), this positive solution states that the existential theory of 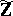 is decidable in a primitive-recursive way (cf. [a6], Chap. 17, for the notion of primitive recursiveness in algebraic geometry). L. van den Dries [a4] has strengthened this result (van den Dries' theorem): The elementary theory of
is decidable in a primitive-recursive way (cf. [a6], Chap. 17, for the notion of primitive recursiveness in algebraic geometry). L. van den Dries [a4] has strengthened this result (van den Dries' theorem): The elementary theory of 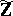 is decidable.
is decidable.
Indeed, van den Dries proves that each statement 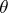 about
about 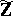 in the language of rings is equivalent to a quantifier-free statement about the parameters of
in the language of rings is equivalent to a quantifier-free statement about the parameters of 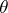 . The latter statement, however, must be written in a language which includes extra predicates, called radicals. They express inclusion between ideals that depend on the parameters of
. The latter statement, however, must be written in a language which includes extra predicates, called radicals. They express inclusion between ideals that depend on the parameters of 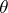 . A special case of the main result of [a11] is an improvement of van den Dries' theorem. It says that the elementary theory of
. A special case of the main result of [a11] is an improvement of van den Dries' theorem. It says that the elementary theory of 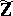 is even primitive recursively decidable. The decision procedure is based on the method of Galois stratification [a6], Chap. 25, adopted to the language of rings with radical relations.
is even primitive recursively decidable. The decision procedure is based on the method of Galois stratification [a6], Chap. 25, adopted to the language of rings with radical relations.
Looking for possible generalizations of the above theorems, van den Dries and A. Macintyre [a3] have axiomatized the elementary theory of 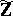 . The axioms are written in the language of rings extended by the "radical relations" mentioned above.
. The axioms are written in the language of rings extended by the "radical relations" mentioned above.
A. Prestel and J. Schmid [a10] take another approach to the radical relations and supply another set of axioms for the elementary theory of 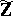 . Their approach yields the following analogue to Hilbert's
. Their approach yields the following analogue to Hilbert's 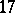 th problem for polynomials over
th problem for polynomials over 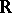 , which was solved by E. Artin and O. Schreier in 1927: Let
, which was solved by E. Artin and O. Schreier in 1927: Let 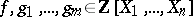 . Then
. Then 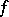 belongs to the radical of the ideal generated by
belongs to the radical of the ideal generated by 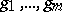 in
in 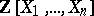 if and only if for all
if and only if for all 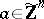 ,
, 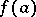 belongs to the radical of the ideal generated by
belongs to the radical of the ideal generated by 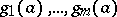 in
in 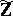 .
.
Needless to say that the proofs of these theorems, as well as the axiomatizations of the elementary theory of 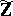 , depend on Rumely's local-global principle.
, depend on Rumely's local-global principle.
The results mentioned above have been strongly generalized in various directions; see also Local-global principles for large rings of algebraic integers.
References
| [a1] | D.C. Cantor, P. Roquette, "On diophantine equations over the ring of all algebraic integers" J. Number Th. , 18 (1984) pp. 1–26 |
| [a2] | E.C. Dade, "Algebraic integral representations by arbitrary forms" Mathematika , 10 (1963) pp. 96–100 (Correction: 11 (1964), 89–90) |
| [a3] | L. van den Dries, A. Macintyre, "The logic of Rumely's local-global principle" J. Reine Angew. Math. , 407 (1990) pp. 33–56 |
| [a4] | L. van den Dries, "Elimination theory for the ring of algebraic integers" J. Reine Angew. Math. , 388 (1988) pp. 189–205 |
| [a5] | D.R. Estes, R.M. Guralnick, "Module equivalence: local to global when primitive polynomials represent units" J. Algebra , 77 (1982) pp. 138–157 |
| [a6] | M.D. Fried, M. Jarden, "Field arithmetic" , Ergebn. Math. III , 11 , Springer (1986) |
| [a7] | B. Green, F. Pop, P. Roquette, "On Rumely's local-global principle" Jahresber. Deutsch. Math. Ver. , 97 (1995) pp. 43–74 |
| [a8] | Y. Matijasevich, "Enumerable sets are diophantine" Soviet Math. Dokl. , 11 (1970) pp. 354–357 (In Russian) |
| [a9] | L. Moret-Bailly, "Groupes de Picard et problèmes de Skolem I" Ann. Sci. Ecole Norm. Sup. , 22 (1989) pp. 161–179 |
| [a10] | A. Prestel, J. Schmid, "Existentially closed domains with radical relations" J. Reine Angew. Math. , 407 (1990) pp. 178–201 |
| [a11] | A. Razon, "Primitive recursive decidability for large rings of algebraic integers" PhD Thesis Tel Aviv (1996) |
| [a12] | R. Rumely, "Arithmetic over the ring of all algebraic integers" J. Reine Angew. Math. , 368 (1986) pp. 127–133 |
| [a13] | R. Rumely, "Capacity theory on algebraic curves" , Lecture Notes Math. , 1378 , Springer (1989) |
| [a14] | Th. Skolem, "Lösung gewisser Gleichungen in ganzen algebraischen Zahlen, insbesondere in Einheiten" Skr. Norske Videnskaps-Akademi Oslo I. Mat. Naturv. Kl. , 10 (1934) |
Local-global principles for the ring of algebraic integers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local-global_principles_for_the_ring_of_algebraic_integers&oldid=18276