Line (curve)
A geometrical concept, of which an exact and at the same time quite general definition presents considerable difficulties and is carried out differently in different branches of geometry.
In elementary geometry the concept of a curve is not clearly defined and is sometimes defined as "length without width" or as the "boundary of a surface" . In elementary geometry the study of a curve essentially reduces to consideration of examples (a straight line, an interval, a polygon, a circle, etc.). Since it does not have general methods at its disposal, elementary geometry has gone quite deeply into the study of properties of specific curves (conic sections, certain algebraic curves of higher orders and transcendental curves), using special methods in each case.
In analytic geometry a curve in a plane is defined as a set of points whose coordinates satisfy an equation 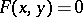 . Restrictions must be imposed on the function
. Restrictions must be imposed on the function 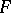 so that, on the one hand, the equation should have an infinite set of solutions and, on the other hand, so that this set of solutions does not fill "a piece of the plane" .
so that, on the one hand, the equation should have an infinite set of solutions and, on the other hand, so that this set of solutions does not fill "a piece of the plane" .
An important class of curves comprises those for which the function 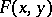 is a polynomial in the two variables; in this case the curve defined by the equation
is a polynomial in the two variables; in this case the curve defined by the equation 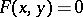 is said to be algebraic. Algebraic curves specified by an equation of the first degree are straight lines. An equation of the second degree that has an infinite set of solutions defines an ellipse, a hyperbola, a parabola, or a curve that splits into two straight lines (which may coincide). Algebraic curves defined by equations of higher degrees are considered in algebraic geometry. Their theory acquires great orderliness if the examination is carried out in the complex projective plane. In this case an algebraic curve is defined by an equation of the form
is said to be algebraic. Algebraic curves specified by an equation of the first degree are straight lines. An equation of the second degree that has an infinite set of solutions defines an ellipse, a hyperbola, a parabola, or a curve that splits into two straight lines (which may coincide). Algebraic curves defined by equations of higher degrees are considered in algebraic geometry. Their theory acquires great orderliness if the examination is carried out in the complex projective plane. In this case an algebraic curve is defined by an equation of the form
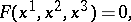 |
where 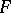 is a homogeneous polynomial in three variables, the projective coordinates of points.
is a homogeneous polynomial in three variables, the projective coordinates of points.
For those branches of mathematics in which the methods of the theory of functions predominate (analysis, differential geometry, etc.) a natural definition of a curve is the specification of it by parametric equations. Thus, in the case of a plane, a curve specified by parametric equations
 | (1) |
where 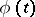 and
and 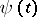 are continuous functions on an interval
are continuous functions on an interval 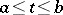 , is the set of points
, is the set of points 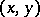 corresponding to all possible values of the parameter
corresponding to all possible values of the parameter 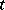 under the condition that these points are considered in a definite order: If the point
under the condition that these points are considered in a definite order: If the point 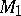 corresponds to the value
corresponds to the value 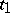 and
and 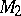 to
to 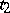 , then
, then 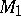 is regarded as preceding
is regarded as preceding 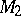 if
if 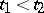 ; points corresponding to distinct values of the parameter are regarded as distinct. The equations
; points corresponding to distinct values of the parameter are regarded as distinct. The equations 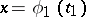 ,
, 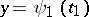 ,
, 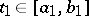 , specify the same curve as equations (1) if there is a homeomorphism
, specify the same curve as equations (1) if there is a homeomorphism 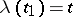 of the interval
of the interval  onto the interval
onto the interval 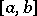 ,
, 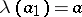 ,
,  , such that
, such that 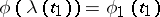 and
and 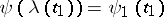 . Similarly, a curve in an arbitrary topological space
. Similarly, a curve in an arbitrary topological space 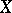 is defined by a parametric equation of the form
is defined by a parametric equation of the form 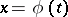 , where
, where 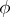 is a function of the real variable
is a function of the real variable 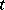 , continuous on
, continuous on 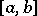 , the values of which are points
, the values of which are points  of
of  .
.
As well as this approach there is another point of view (C. Jordan, 1882) on the definition of a curve by parametric equations: A curve is a set of points of the plane whose coordinates are continuous functions 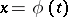 ,
, 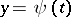 of the parameter
of the parameter 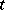 specified on an interval
specified on an interval 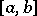 ; now points corresponding to distinct values of the parameter but having the same coordinates are not regarded as distinct, and the set comprising a curve is not regarded as ordered by values of
; now points corresponding to distinct values of the parameter but having the same coordinates are not regarded as distinct, and the set comprising a curve is not regarded as ordered by values of 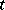 . This definition can be generalized to any topological space: A set of points of a topological space that is a continuous image of an interval is called a curve in the sense of Jordan.
. This definition can be generalized to any topological space: A set of points of a topological space that is a continuous image of an interval is called a curve in the sense of Jordan.
However, continuous functions 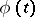 and
and 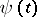 ,
, 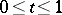 , have been constructed so that the set of points whose coordinates are determined by these functions fill the square
, have been constructed so that the set of points whose coordinates are determined by these functions fill the square 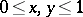 (see Peano curve). More generally, any locally connected continuum (that is, a continuum each point of which has an arbitrary small connected neighbourhood) is a continuous image of an interval (a theorem of Mazurkiewicz). Thus, not only a square, but also a cube of arbitrary dimension and even the infinite-dimensional Hilbert cube are continuous images of an interval.
(see Peano curve). More generally, any locally connected continuum (that is, a continuum each point of which has an arbitrary small connected neighbourhood) is a continuous image of an interval (a theorem of Mazurkiewicz). Thus, not only a square, but also a cube of arbitrary dimension and even the infinite-dimensional Hilbert cube are continuous images of an interval.
The above-said shows that a curve cannot be defined as a continuous image of an interval if one does not impose additional restrictions on the mapping. Thus, in differential geometry these restrictions are given by imposing conditions for the existence of derivatives of various orders of the functions that occur in the parametric definition of a curve. On the other hand, there are continua that can naturally be regarded as curves but which, not being locally connected, are not continuous images of an interval. Such, for example, is the continuum defined by the conditions:  ,
, 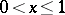 ;
; 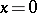 ,
, 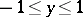 (Fig. a).
(Fig. a).
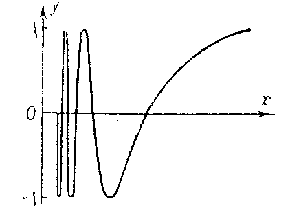
Figure: l059020a
A more general definition of a curve for the case of a plane was given by G. Cantor in the 1870's in connection with the creation of the theory of point sets. A planar continuum such that in any neighbourhood of each point of it there are points of the plane that do not belong to the continuum is called a Cantor curve. An important example of a Cantor curve is the Sierpiński carpet, constructed as follows. A square 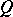 of sides 1 is divided into nine equal squares by straight lines parallel to its sides, and all the interior points of the central square are removed (Fig. b,
of sides 1 is divided into nine equal squares by straight lines parallel to its sides, and all the interior points of the central square are removed (Fig. b, 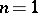 ). The same is done with each of the remaining eight squares of the first rank, and one obtains 64 squares of the second rank (Fig. b,
). The same is done with each of the remaining eight squares of the first rank, and one obtains 64 squares of the second rank (Fig. b, 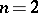 ). Continuing the process for all natural numbers
). Continuing the process for all natural numbers  , at the
, at the  -th step one obtains
-th step one obtains 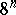 squares of the
squares of the  -th rank with sides
-th rank with sides  . The intersection of the sets obtained in this way is the Sierpiński carpet (Fig. b).
. The intersection of the sets obtained in this way is the Sierpiński carpet (Fig. b).
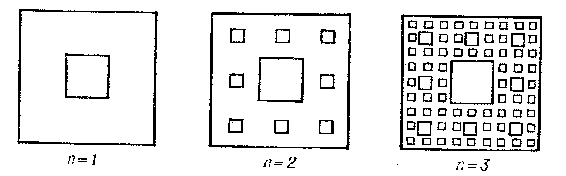
Figure: l059020b
Whatever Cantor curve 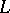 one has, it can be topologically imbedded in the Sierpiński carpet
one has, it can be topologically imbedded in the Sierpiński carpet 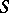 , that is, in
, that is, in 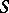 there is a continuum
there is a continuum 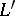 homeomorphic to
homeomorphic to 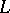 . The Sierpiński carpet is a locally connected continuum and so it is a continuous image of an interval.
. The Sierpiński carpet is a locally connected continuum and so it is a continuous image of an interval.
In topology one uses the concept of a curve introduced in 1921 by P.S. Urysohn, which is more general (but not excessively so). The definition of a curve is stated as follows: A curve is a one-dimensional continuum, that is, a connected compact metric space 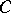 each point of which has an arbitrary small neighbourhood with a boundary of dimension zero. In other words, for any
each point of which has an arbitrary small neighbourhood with a boundary of dimension zero. In other words, for any 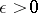 the space
the space 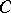 can be represented as the sum of finitely many closed sets of diameter less than
can be represented as the sum of finitely many closed sets of diameter less than  having the property that no three of these sets have a common point. The Sierpiński carpet satisfies this definition of a curve, so any Cantor curve is also a curve in the sense of Urysohn. Conversely, if a planar continuum is a curve in the sense of Urysohn, then it is a Cantor curve. The definition of a curve given by Urysohn is intrinsic: It is characterized only by properties of the space
having the property that no three of these sets have a common point. The Sierpiński carpet satisfies this definition of a curve, so any Cantor curve is also a curve in the sense of Urysohn. Conversely, if a planar continuum is a curve in the sense of Urysohn, then it is a Cantor curve. The definition of a curve given by Urysohn is intrinsic: It is characterized only by properties of the space 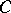 itself and does not depend on whether this space is considered in itself or as a subset of another topological space.
itself and does not depend on whether this space is considered in itself or as a subset of another topological space.
There are curves that are not homeomorphic to any subset of the plane. Such, for example, is the curve lying in the three-dimensional space and consisting of the six edges of a tetrahedron and the four segments joining a point of the space not lying on one of its faces to its vertices (Fig. c).
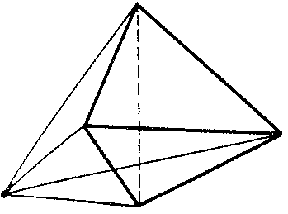
Figure: l059020c
However, any curve (in the sense of Urysohn) is homeomorphic to a subset of the three-dimensional Euclidean space (Menger's theorem). A continuum 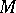 having the property that whatever the curve
having the property that whatever the curve 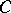 there is a subcontinuum
there is a subcontinuum  of
of 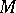 homeomorphic to
homeomorphic to 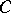 , is constructed as follows. A cube
, is constructed as follows. A cube 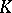 of edges 1 is divided by planes parallel to its faces into 27 equal cubes. From
of edges 1 is divided by planes parallel to its faces into 27 equal cubes. From 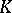 one removes the central cube and all cubes of this subdivision adjacent to it along two-dimensional faces. One obtains a set
one removes the central cube and all cubes of this subdivision adjacent to it along two-dimensional faces. One obtains a set 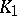 consisting of the remaining 20 closed cubes of the first rank. Doing exactly the same with each cube of the first rank, one obtains a set
consisting of the remaining 20 closed cubes of the first rank. Doing exactly the same with each cube of the first rank, one obtains a set 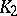 consisting of 400 cubes of the second rank (Fig. d). Continuing this process indefinitely, one obtains a sequence of continua
consisting of 400 cubes of the second rank (Fig. d). Continuing this process indefinitely, one obtains a sequence of continua 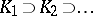 the intersection of which is a one-dimensional continuum
the intersection of which is a one-dimensional continuum 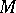 , called the Menger universal curve.
, called the Menger universal curve.
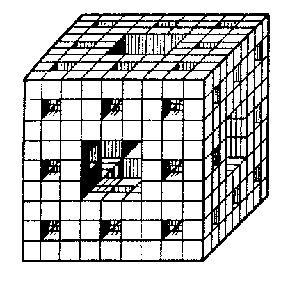
Figure: l059020d
In the investigation of curves an important role is played by the concept of the ramification index. A curve 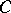 at a point
at a point  has ramification index
has ramification index 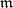 if for any number
if for any number 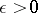 there is an open set
there is an open set 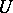 of diameter less than
of diameter less than  whose boundary is a set of cardinality at most
whose boundary is a set of cardinality at most 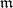 , but for any sufficiently small
, but for any sufficiently small 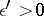 the boundary of any open set, containing
the boundary of any open set, containing  , whose diameter is less than
, whose diameter is less than 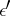 has cardinality not less than
has cardinality not less than 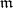 . Points of a curve are classified with respect to their ramification index as follows.
. Points of a curve are classified with respect to their ramification index as follows.
1) Points with ramification index  , where
, where  is a natural number.
is a natural number.
2) Points of unbounded ramification index 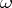 . (A point
. (A point  of a curve
of a curve 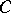 has ramification index
has ramification index 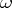 if for any number
if for any number  there is an open set, containing
there is an open set, containing  , with diameter less than
, with diameter less than  and whose boundary consists of a finite set of points, and if for any natural number
and whose boundary consists of a finite set of points, and if for any natural number  there is a number
there is a number 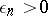 such that the boundary of any open set containing
such that the boundary of any open set containing  and having diameter less than
and having diameter less than 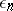 consists of at least
consists of at least  points.)
points.)
3) Points of countable ramification index 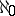 .
.
4) Points of continual ramification index  .
.
A point of a curve 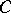 of ramification index larger than two is called a ramification point; a point with ramification index one is called an end point.
of ramification index larger than two is called a ramification point; a point with ramification index one is called an end point.
Examples. a) At all its interior points an interval has ramification index equal to two; the ramification index of each end of the interval is equal to one. b) At each of its points a circle has ramification index two. c) A curve consisting of  rectilinear intervals starting from one point
rectilinear intervals starting from one point 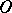 has ramification index
has ramification index  at
at 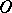 . d) A curve consisting of intervals
. d) A curve consisting of intervals 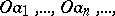 starting from the origin
starting from the origin 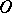 and having lengths
and having lengths 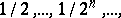 and making angles with the
and making angles with the  -axis respectively equal to
-axis respectively equal to 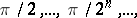 has unboundedly increasing ramification index
has unboundedly increasing ramification index 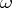 at
at 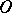 (Fig. e).
(Fig. e).
Figure: l059020e
Figure: l059020f
e) A curve consisting of the interval 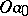 of length
of length  and intervals
and intervals 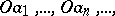 of length
of length 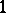 starting from
starting from 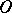 and making angles with
and making angles with 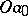 respectively equal to
respectively equal to  has countable ramification index
has countable ramification index 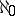 at each point of
at each point of 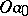 (Fig. f). f) A curve consisting of intervals joining
(Fig. f). f) A curve consisting of intervals joining 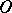 to all points of a Cantor set lying on the interval
to all points of a Cantor set lying on the interval 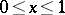 ,
, 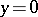 , has continual ramification index
, has continual ramification index  at each of its points (Fig. g).
at each of its points (Fig. g).
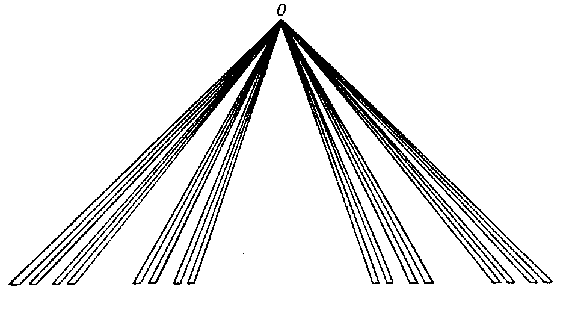
Figure: l059020g
g) The Sierpiński carpet also has continual ramification index at each of its points.
If a curve has no ramification points at all, that is, if at each point of the curve the ramification index is equal to 1 or 2, then this curve is either a simple arc (the topological image of an interval) or a simple closed curve (the topological image of a circle). If the ramification index of a curve at all points is equal to two, then it is a simple closed curve, and if a curve that does not have ramification points has end points (it turns out that there are invariably two of them), then it is a simple arc. If a curve has only finitely many ramification points and the ramification index of each of them is also finite, then such a curve can be split into finitely many simple arcs having no common points except their end points.
A circle is the only curve all points of which have the same finite ramification index 2; there are no other curves having the same finite ramification index at all points, and if all points of a curve 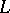 have ramification index greater than or equal to
have ramification index greater than or equal to  , then there is a point on
, then there is a point on 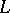 with ramification index greater than or equal to
with ramification index greater than or equal to 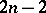 ; for any natural number
; for any natural number  there is a curve consisting only of points having ramification index
there is a curve consisting only of points having ramification index  and
and 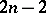 (Urysohn's theorem). An example of a curve consisting only of points with ramification index 3 or 4 is constructed as follows.
(Urysohn's theorem). An example of a curve consisting only of points with ramification index 3 or 4 is constructed as follows.
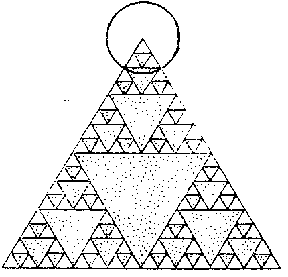
Figure: l059020h
In an equilateral triangle with sides 1 one draws the three lines joining the midpoints, and from it one removes the interior points of the triangle formed by them. With each of the remaining three triangles of the first rank one carries out a similar operation, as a result of which one obtains nine triangles of the second rank. Proceeding in the same way with these, one obtains 27 triangles of the third rank, etc. for every natural number  . The intersection of the sets obtained as a result of these operations is a curve
. The intersection of the sets obtained as a result of these operations is a curve 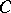 (Fig. h). A curve consisting of points with ramification index 3 or 4 consists of two continua
(Fig. h). A curve consisting of points with ramification index 3 or 4 consists of two continua 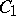 and
and 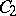 , each of which is homeomorphic to
, each of which is homeomorphic to 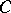 and which have no points in common other than those corresponding to the vertices of the basic triangle of the continuum
and which have no points in common other than those corresponding to the vertices of the basic triangle of the continuum 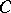 .
.
There are also curves that have unbounded ramification index, countable ramification index and continual ramification index at all points.
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [2] | K. Kuratowski, "Topology" , 2 , Acad. Press (1968) (Translated from French) |
| [3] | K. Menger, "Kurventheorie" , Teubner (1932) |
| [4] | A.S. Parkhomenko, "What is a curve?" , Moscow (1954) (In Russian) |
| [5] | P.S. Urysohn, "Works on topology and other areas of mathematics" , 2 , Moscow-Leningrad (1951) (In Russian) |
| [6] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
Comments
A "curve in the sense of Jordan" (that is, a continuous image of the unit interval 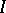 ) is also called a Peano continuum. It should not be mixed up with the notion of a Jordan curve (a space homeomorphic to the circle, also called a simple closed curve).
) is also called a Peano continuum. It should not be mixed up with the notion of a Jordan curve (a space homeomorphic to the circle, also called a simple closed curve).
The theorem of Mazurkiewicz mentioned above is generally known as the Hahn–Mazurkiewicz theorem [a1], 6.3.14.
Sierpiński's carpet is also called Sierpiński's universal curve.
The curve in Fig. hwas constructed by W. Sierpiński [a3].
References
| [a1] | R. Engelking, "General topology" , Heldermann (1989) |
| [a2] | R. Engelking, "Dimension theory" , North-Holland & PWN (1978) pp. 19; 50 |
| [a3] | W. Sierpiński, "Sur un courbe dont tout point est un point de ramification" C.R. Hebdomaires Acad. Sci. Paris , 160 (1915) pp. 302–305 |
| [a4] | L. Blumenthal, K. Menger, "Studies in geometry" , Freeman (1970) (Translated from German) |
| [a5] | J.L. Coolidge, "A treatise on algebraic plane curves" , Clarendon Press (1931) |
| [a6] | A.D. [A.D. Aleksandrov] Alexandrov, Yu.G. Reshetnyak, "General theory of irregular curves" , Kluwer (1989) (Translated from Russian) |
Line (curve). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Line_(curve)&oldid=15722