Difference between revisions of "Inverse function"
(Importing text file) |
m |
||
| Line 1: | Line 1: | ||
| + | {{TEX|want}} | ||
| + | |||
The function that associates with each of the elements of the set of values of a given function the set of all elements from the domain of definition of the given function that are mapped onto it, that is, its complete inverse image. If the given function is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523601.png" />, then the inverse function is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523602.png" />. Thus, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523603.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523604.png" /> is the range of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523605.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523606.png" />, then for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523607.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523608.png" />. | The function that associates with each of the elements of the set of values of a given function the set of all elements from the domain of definition of the given function that are mapped onto it, that is, its complete inverse image. If the given function is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523601.png" />, then the inverse function is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523602.png" />. Thus, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523603.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523604.png" /> is the range of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523605.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523606.png" />, then for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523607.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052360/i0523608.png" />. | ||
Revision as of 17:20, 26 February 2013
The function that associates with each of the elements of the set of values of a given function the set of all elements from the domain of definition of the given function that are mapped onto it, that is, its complete inverse image. If the given function is denoted by  , then the inverse function is denoted by
, then the inverse function is denoted by  . Thus, if
. Thus, if  and
and  is the range of
is the range of  ,
,  , then for any
, then for any  one has
one has  .
.
If for all  the complete inverse image of
the complete inverse image of 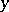 consists of precisely one element
consists of precisely one element  , that is, if the mapping
, that is, if the mapping 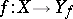 is a bijection, then the inverse function is single-valued, otherwise it is many-valued.
is a bijection, then the inverse function is single-valued, otherwise it is many-valued.
If the sets 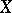 and
and  are subsets of the real line (or, more generally, of some ordered sets) then strict monotonicity of
are subsets of the real line (or, more generally, of some ordered sets) then strict monotonicity of 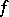 is a necessary and sufficient condition for the existence of an inverse function that is also strictly monotone.
is a necessary and sufficient condition for the existence of an inverse function that is also strictly monotone.
A number of properties of the inverse function can be determined from the corresponding properties of 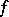 . For example, if
. For example, if  is strictly monotone and continuous on some interval of the real line, then its inverse is also monotone and continuous on the corresponding interval. If a one-to-one mapping of a compactum onto a Hausdorff topological space is continuous, then the inverse mapping is also continuous. That is, the original mapping is a homeomorphism onto its image. When the mapping
is strictly monotone and continuous on some interval of the real line, then its inverse is also monotone and continuous on the corresponding interval. If a one-to-one mapping of a compactum onto a Hausdorff topological space is continuous, then the inverse mapping is also continuous. That is, the original mapping is a homeomorphism onto its image. When the mapping  is a one-to-one bounded linear operator mapping a Banach space
is a one-to-one bounded linear operator mapping a Banach space  onto a Banach space
onto a Banach space 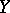 , then the inverse operator
, then the inverse operator 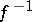 is also linear and bounded.
is also linear and bounded.
Let 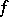 be a continuous mapping of the closure
be a continuous mapping of the closure 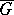 of a bounded domain
of a bounded domain 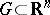 ,
, 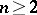 , with a sufficiently smooth boundary in
, with a sufficiently smooth boundary in 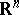 , let
, let 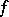 be differentiable in
be differentiable in 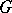 and map the boundary of
and map the boundary of  onto the boundary of
onto the boundary of 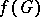 and suppose that the set of zeros of the Jacobian of
and suppose that the set of zeros of the Jacobian of  is an isolated set; then if
is an isolated set; then if  is one-to-one on the boundary of
is one-to-one on the boundary of 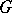 , it is one-to-one on
, it is one-to-one on  . For the existence of a local inverse mapping in a neighbourhood of a given point it is sufficient that the Jacobian of the mapping does not vanish in some neighbourhood of this point. If
. For the existence of a local inverse mapping in a neighbourhood of a given point it is sufficient that the Jacobian of the mapping does not vanish in some neighbourhood of this point. If  ,
, 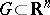 , is a differentiable mapping with non-zero Jacobian at all points
, is a differentiable mapping with non-zero Jacobian at all points 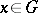 , then for any
, then for any 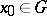 there exists a neighbourhood
there exists a neighbourhood  such that the restriction
such that the restriction  of
of 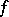 to
to 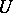 is a one-to-one mapping of
is a one-to-one mapping of 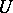 onto some neighbourhood
onto some neighbourhood 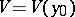 of
of  , and the inverse mapping
, and the inverse mapping 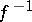 is also differentiable (on
is also differentiable (on 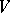 ). This theorem can be generalized to the infinite-dimensional case: Let
). This theorem can be generalized to the infinite-dimensional case: Let 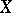 and
and  be complete normed spaces, let
be complete normed spaces, let  be an open set and let
be an open set and let 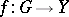 be a continuously-differentiable mapping. If
be a continuously-differentiable mapping. If 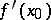 is an invertible element in the space of bounded linear operators
is an invertible element in the space of bounded linear operators 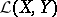 (
(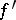 is the Fréchet derivative),
is the Fréchet derivative), 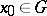 , then there exists neighbourhoods
, then there exists neighbourhoods  and
and  of
of 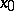 and
and 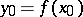 in
in  and
and 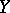 respectively, such that the mapping
respectively, such that the mapping 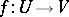 and its inverse mapping are continuously-differentiable homeomorphisms.
and its inverse mapping are continuously-differentiable homeomorphisms.
References
| [1] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
Comments
The assertions in the last paragraph of the main article are known under the (collective) name of inverse-function theorem.
Nowadays the term "function" is usually reserved for those relations that are single-valued, and the term "mapping" is one of its synonyms. When this is done, only bijections (one-to-one onto functions) have inverses that are functions. In all other cases, the inverse relation  (called a many-valued function in the main article) is not a function unless, as is sometimes done, it is regarded as being set-valued. Then arises the important but simple distinction between a singleton set and its unique element.
(called a many-valued function in the main article) is not a function unless, as is sometimes done, it is regarded as being set-valued. Then arises the important but simple distinction between a singleton set and its unique element.
Inverse function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inverse_function&oldid=29492