Infinite-dimensional representation
of a Lie group
A representation of a Lie group (cf. Representation of a topological group) in an infinite-dimensional vector space. The theory of representations of Lie groups is part of the general theory of representations of topological groups. The specific features of Lie groups make it possible to employ analytical tools in this theory (in particular, infinitesimal methods), and also to considerably enlarge the class of "natural" group algebras (function algebras with respect to convolution, cf. Group algebra), the study of which connects this theory with abstract harmonic analysis, i.e. with part of the general theory of topological algebras (cf. Harmonic analysis, abstract; Topological algebra).
Let 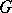 be a Lie group. A representation of
be a Lie group. A representation of 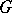 in a general sense is any homomorphism
in a general sense is any homomorphism 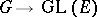 , where GL
, where GL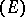 is the group of all invertible linear transformations of the vector space
is the group of all invertible linear transformations of the vector space 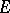 . If
. If 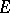 is a topological vector space, the homomorphisms which are usually considered are those with values in the algebra
is a topological vector space, the homomorphisms which are usually considered are those with values in the algebra 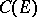 of all continuous linear transformations of
of all continuous linear transformations of 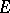 or in the algebra
or in the algebra 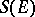 of all weakly-continuous transformations of
of all weakly-continuous transformations of 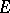 . The algebras
. The algebras 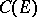 and
and 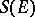 have one of the standard topologies (for example, the weak or the strong). A representation
have one of the standard topologies (for example, the weak or the strong). A representation 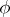 is said to be continuous (separately continuous) if the vector function
is said to be continuous (separately continuous) if the vector function 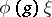 is continuous (separately continuous) on
is continuous (separately continuous) on 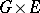 . If
. If 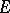 is a quasi-complete barrelled space, any separately continuous representation is continuous. A continuous representation
is a quasi-complete barrelled space, any separately continuous representation is continuous. A continuous representation 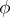 is called differentiable (analytic) if the operator function
is called differentiable (analytic) if the operator function 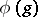 is differentiable (analytic) on
is differentiable (analytic) on 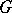 . The dimension of a representation
. The dimension of a representation 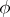 is the dimension of
is the dimension of 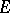 . The most important example of a representation of a group
. The most important example of a representation of a group 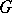 is its regular representation
is its regular representation 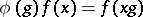 ,
, 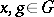 , which can be defined on some class of functions
, which can be defined on some class of functions 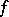 on
on 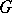 . If
. If 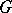 is a Lie group, its regular representation is continuous in
is a Lie group, its regular representation is continuous in 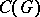 and in
and in 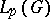 (where
(where 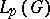 is defined with respect to the Haar measure on
is defined with respect to the Haar measure on 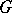 ), and is differentiable in
), and is differentiable in 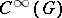 (with respect to the standard topology in
(with respect to the standard topology in 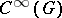 : the topology of compact convergence). Every continuous finite-dimensional representation of a group
: the topology of compact convergence). Every continuous finite-dimensional representation of a group 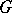 is analytic. If
is analytic. If 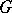 is a complex Lie group, it is natural to consider its complex-analytic (holomorphic) representations as well. As a rule, only continuous representations are considered in the theory of representations of Lie groups, and the continuity condition is not explicitly stipulated. If the group
is a complex Lie group, it is natural to consider its complex-analytic (holomorphic) representations as well. As a rule, only continuous representations are considered in the theory of representations of Lie groups, and the continuity condition is not explicitly stipulated. If the group 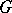 is compact, all its irreducible (continuous) representations are finite-dimensional. Similarly, if
is compact, all its irreducible (continuous) representations are finite-dimensional. Similarly, if 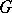 is a semi-simple complex Lie group, all its irreducible holomorphic representations are finite-dimensional.
is a semi-simple complex Lie group, all its irreducible holomorphic representations are finite-dimensional.
Relation to representations of group algebras.
The most important group algebras for Lie groups are the algebra 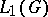 ; the algebra
; the algebra 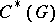 , which is the completion of
, which is the completion of 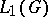 in the smallest regular norm (cf. Algebra of functions);
in the smallest regular norm (cf. Algebra of functions); 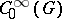 — the algebra of all infinitely-differentiable functions on
— the algebra of all infinitely-differentiable functions on 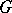 with compact support;
with compact support; 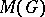 — the algebra of all complex Radon measures with compact support on
— the algebra of all complex Radon measures with compact support on 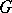 ;
; 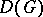 — the algebra of all generalized functions (Schwarz distributions) on G with compact support; and also, for a complex Lie group, the algebra
— the algebra of all generalized functions (Schwarz distributions) on G with compact support; and also, for a complex Lie group, the algebra 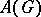 of all analytic functionals over
of all analytic functionals over 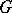 . The linear spaces
. The linear spaces 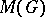 ,
, 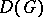 ,
, 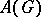 are dual to, respectively,
are dual to, respectively, 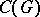 ,
, 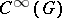 ,
, 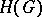 , where
, where 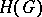 is the set of all holomorphic functions on
is the set of all holomorphic functions on 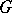 (with the topology of compact convergence). All these algebras have a natural topology. In particular,
(with the topology of compact convergence). All these algebras have a natural topology. In particular, 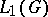 is a Banach algebra. The product (convolution) of two elements
is a Banach algebra. The product (convolution) of two elements 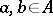 , where
, where 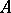 is one of the group algebras indicated above, is defined by the equality
is one of the group algebras indicated above, is defined by the equality
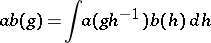 |
with respect to a right-invariant measure on 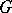 , with a natural extension of this operation to the class of generalized functions. The integral formula
, with a natural extension of this operation to the class of generalized functions. The integral formula
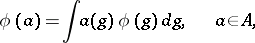 |
establishes a natural connection between the representations of the group 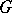 and the representations of the algebra
and the representations of the algebra 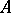 (if the integral is correctly defined): If the integral is weakly convergent and defines an operator
(if the integral is correctly defined): If the integral is weakly convergent and defines an operator 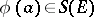 for each
for each 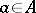 , then the mapping
, then the mapping 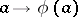 is a homomorphism. One then says that the representation
is a homomorphism. One then says that the representation 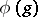 of the group
of the group 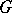 is extended to the representation
is extended to the representation 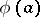 of the algebra
of the algebra 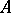 , or that it is an
, or that it is an 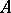 -representation. Conversely, all weakly-continuous non-degenerate representations of the algebra
-representation. Conversely, all weakly-continuous non-degenerate representations of the algebra 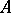 are determined, in accordance with the formula above, by some representation of the group
are determined, in accordance with the formula above, by some representation of the group 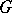 (weakly continuous for
(weakly continuous for 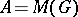 , weakly differentiable for
, weakly differentiable for 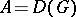 , weakly analytic for
, weakly analytic for 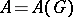 ). This correspondence preserves all natural relations between the representations, such as topological irreducibility or equivalence. If
). This correspondence preserves all natural relations between the representations, such as topological irreducibility or equivalence. If 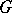 is a unimodular group, its unitary representations (in Hilbert spaces, cf. Unitary representation) correspond to symmetric representations of the algebra
is a unimodular group, its unitary representations (in Hilbert spaces, cf. Unitary representation) correspond to symmetric representations of the algebra 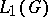 with respect to the involution in
with respect to the involution in 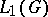 (cf. Group algebra; Involution representation). If
(cf. Group algebra; Involution representation). If 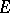 is a sequentially complete, locally convex Hausdorff space, any continuous representation of a group
is a sequentially complete, locally convex Hausdorff space, any continuous representation of a group 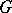 in
in 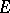 is an
is an 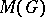 -representation. If, moreover, the representation of the group
-representation. If, moreover, the representation of the group 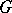 is differentiable, it is a
is differentiable, it is a 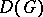 -representation. In particular, if
-representation. In particular, if 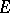 is a reflexive or a quasi-complete barrelled space, any separately-continuous representation
is a reflexive or a quasi-complete barrelled space, any separately-continuous representation 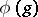 is an
is an 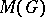 -representation, and
-representation, and  for all
for all 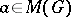 .
.
The infinitesimal method.
If a representation 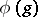 is differentiable, it is infinitely often differentiable, and the space
is differentiable, it is infinitely often differentiable, and the space 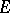 has the structure of a
has the structure of a 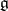 -module, where
-module, where 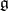 is the Lie algebra of the group
is the Lie algebra of the group 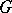 , by considering the Lie infinitesimal operators:
, by considering the Lie infinitesimal operators:
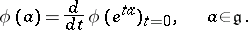 |
The operators 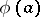 form a representation of the algebra
form a representation of the algebra 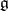 , called the differential representation
, called the differential representation 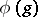 . A vector
. A vector 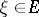 is said to be differentiable (with respect to
is said to be differentiable (with respect to 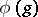 ) if the vector function
) if the vector function 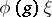 is differentiable on
is differentiable on 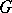 . A vector
. A vector 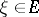 is said to be analytic if
is said to be analytic if 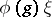 is an analytic function in a neighbourhood of the unit
is an analytic function in a neighbourhood of the unit 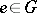 . If
. If 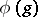 is a
is a 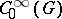 -representation, the space
-representation, the space 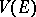 of all infinitely-differentiable vectors is everywhere-dense in
of all infinitely-differentiable vectors is everywhere-dense in  . In particular, this is true for all continuous representations in a Banach space; moreover, in this case [4] the space
. In particular, this is true for all continuous representations in a Banach space; moreover, in this case [4] the space 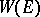 of analytic vectors is everywhere-dense in
of analytic vectors is everywhere-dense in 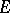 . The differential representation
. The differential representation 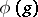 in
in 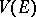 may be reducible, even if
may be reducible, even if 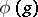 is topologically irreducible in
is topologically irreducible in 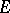 . To two equivalent representations of
. To two equivalent representations of 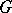 correspond equivalent differential representations in
correspond equivalent differential representations in 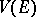 (
(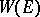 ); the converse is, generally speaking, not true. For unitary representations in Hilbert spaces
); the converse is, generally speaking, not true. For unitary representations in Hilbert spaces 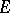 ,
, 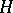 it follows from the equivalence of differential representations in
it follows from the equivalence of differential representations in 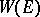 ,
, 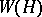 that the representations are equivalent [7]. In the finite-dimensional case a representation of a connected Lie group can be uniquely reproduced from its differential representation. A representation of the algebra
that the representations are equivalent [7]. In the finite-dimensional case a representation of a connected Lie group can be uniquely reproduced from its differential representation. A representation of the algebra 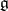 is said to be integrable (
is said to be integrable (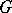 -integrable) if it coincides with a differential representation of the group
-integrable) if it coincides with a differential representation of the group 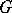 in a subspace which is everywhere-dense in the representation space. Integrability criteria are now (1988) known only in isolated cases [4]. If
in a subspace which is everywhere-dense in the representation space. Integrability criteria are now (1988) known only in isolated cases [4]. If 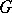 is simply connected, all finite-dimensional representations of the algebra
is simply connected, all finite-dimensional representations of the algebra 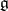 are
are 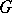 -integrable.
-integrable.
Irreducible representations.
One of the main tasks of the theory of representations is the classification of all irreducible representations (cf. Irreducible representation) of a given group 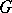 , defined up to an equivalence, using a suitable definition of the concepts of irreducibility and equivalence. Thus, the following two problems are of interest: 1) the description of the set
, defined up to an equivalence, using a suitable definition of the concepts of irreducibility and equivalence. Thus, the following two problems are of interest: 1) the description of the set 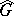 of all unitary equivalence classes of irreducible unitary representations of a group
of all unitary equivalence classes of irreducible unitary representations of a group 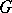 ; and 2) the description of the set
; and 2) the description of the set 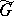 of all Fell equivalence classes [7] of totally-irreducible representations (also called completely-irreducible representations) of a group
of all Fell equivalence classes [7] of totally-irreducible representations (also called completely-irreducible representations) of a group  . For semi-simple Lie groups with a finite centre, Fell equivalence is equivalent to Naimark equivalence [7], and the natural imbedding
. For semi-simple Lie groups with a finite centre, Fell equivalence is equivalent to Naimark equivalence [7], and the natural imbedding 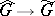 holds. The sets
holds. The sets 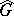 ,
, 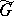 have a natural topology, and their topologies are not necessarily Hausdorff [5]. If
have a natural topology, and their topologies are not necessarily Hausdorff [5]. If 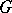 is a compact Lie group, then
is a compact Lie group, then 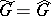 is a discrete space. The description of the set
is a discrete space. The description of the set 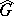 in such a case is due to E. Cartan and H. Weyl. The linear envelope
in such a case is due to E. Cartan and H. Weyl. The linear envelope 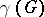 of matrix entries of the group
of matrix entries of the group 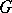 (i.e. of matrix entries of the representations
(i.e. of matrix entries of the representations 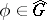 ) here forms a subalgebra in
) here forms a subalgebra in 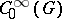 (the algebra of spherical functions) which is everywhere-dense in
(the algebra of spherical functions) which is everywhere-dense in 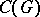 and in
and in 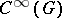 . The matrix entries form a basis in
. The matrix entries form a basis in 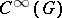 . If the matrices of all representations
. If the matrices of all representations 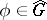 are defined in a basis with respect to which they are unitary, the corresponding matrix entries form an orthogonal basis in
are defined in a basis with respect to which they are unitary, the corresponding matrix entries form an orthogonal basis in 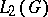 ( the Peter–Weyl theorem). If the group
( the Peter–Weyl theorem). If the group 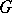 is not compact, its irreducible representations are usually infinite-dimensional. A method for constructing such representations analogous to the classical matrix groups was proposed by I.M. Gel'fand and M.A. Naimark [1], and became the starting point of an intensive development of the theory of unitary infinite-dimensional representations. G.W. Mackey's [5] theory of induced representations is a generalization of this method to arbitrary Lie groups. The general theory of non-unitary representations in locally convex vector spaces, which began to develop in the 1950's, is based to a great extent on the theory of topological vector spaces and on the theory of generalized functions. A detailed description of
is not compact, its irreducible representations are usually infinite-dimensional. A method for constructing such representations analogous to the classical matrix groups was proposed by I.M. Gel'fand and M.A. Naimark [1], and became the starting point of an intensive development of the theory of unitary infinite-dimensional representations. G.W. Mackey's [5] theory of induced representations is a generalization of this method to arbitrary Lie groups. The general theory of non-unitary representations in locally convex vector spaces, which began to develop in the 1950's, is based to a great extent on the theory of topological vector spaces and on the theory of generalized functions. A detailed description of 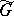 (
(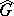 ) is known (1988) for isolated classes of Lie groups (semi-simple complex, nilpotent and certain solvable Lie groups, as well as for their semi-direct products).
) is known (1988) for isolated classes of Lie groups (semi-simple complex, nilpotent and certain solvable Lie groups, as well as for their semi-direct products).
Let 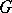 be a semi-simple Lie group with a finite centre, let
be a semi-simple Lie group with a finite centre, let 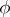 be an
be an 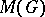 -representation in the space
-representation in the space 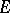 and let
and let  be a compact subgroup in
be a compact subgroup in 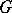 . A vector
. A vector 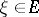 is said to be
is said to be 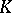 -finite if its cyclic envelope is finite-dimensional with respect to
-finite if its cyclic envelope is finite-dimensional with respect to 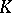 . The subspace
. The subspace 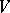 of all
of all 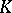 -finite vectors is everywhere-dense in
-finite vectors is everywhere-dense in 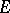 and is the direct (algebraic) sum of subspaces
and is the direct (algebraic) sum of subspaces 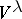 ,
, 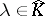 , where
, where 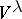 is the maximal subspace in
is the maximal subspace in 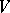 in which the representation of
in which the representation of 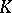 is a multiple of
is a multiple of 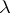 . A representation
. A representation 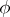 is said to be
is said to be 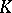 -finite if
-finite if 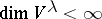 for all
for all 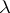 . A subgroup
. A subgroup 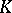 is said to be massive (large or rich) if every totally-irreducible representation of
is said to be massive (large or rich) if every totally-irreducible representation of 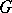 is
is 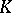 -finite. The following fact is of paramount importance in the theory of representations: If
-finite. The following fact is of paramount importance in the theory of representations: If 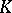 is a maximal compact subgroup in
is a maximal compact subgroup in 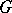 , then
, then 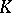 is massive. If the vectors of
is massive. If the vectors of  are differentiable,
are differentiable, 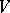 is invariant with respect to the differential
is invariant with respect to the differential 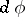 of the representation
of the representation 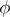 . The representation
. The representation 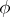 is said to be normal if it is
is said to be normal if it is 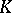 -finite and if the vectors of
-finite and if the vectors of 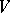 are weakly analytic. If
are weakly analytic. If 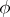 is normal, there exists a one-to-one mapping (defined by restriction to
is normal, there exists a one-to-one mapping (defined by restriction to 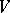 ) between closed submodules of the
) between closed submodules of the 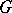 -module
-module 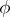 and submodules of the
and submodules of the 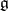 -module
-module 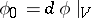 , where
, where 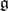 is the Lie algebra of the group
is the Lie algebra of the group 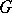 [7]. Thus, the study of normal representations can be algebraized by the infinitesimal method. An example of a normal representation of the group
[7]. Thus, the study of normal representations can be algebraized by the infinitesimal method. An example of a normal representation of the group 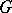 is its principal series representation
is its principal series representation 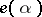 . This representation is totally irreducible for points
. This representation is totally irreducible for points 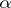 in general position. In the general case
in general position. In the general case 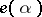 can be decomposed into a finite composition series the factors of which are totally irreducible. Any quasi-simple irreducible representation of the group
can be decomposed into a finite composition series the factors of which are totally irreducible. Any quasi-simple irreducible representation of the group 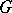 in a Banach space is infinitesimally equivalent to one of the factors of
in a Banach space is infinitesimally equivalent to one of the factors of 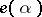 for a given
for a given 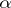 . This is also true for totally-irreducible representations of
. This is also true for totally-irreducible representations of 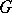 in quasi-complete locally convex spaces. If
in quasi-complete locally convex spaces. If 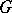 is real or complex, it is sufficient to consider subrepresentations of
is real or complex, it is sufficient to consider subrepresentations of 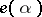 instead of its factors [7]. In the simplest case of
instead of its factors [7]. In the simplest case of 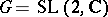 , the representation
, the representation 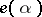 is defined by a pair of complex numbers
is defined by a pair of complex numbers 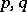 with integral difference
with integral difference 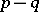 , and operates in accordance with the right-shift formula
, and operates in accordance with the right-shift formula 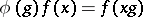 ,
, 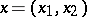 ,
, 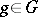 , on the space of all functions
, on the space of all functions 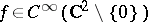 which satisfy the homogeneity condition
which satisfy the homogeneity condition 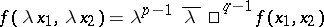 . If
. If  and
and  are positive integers,
are positive integers,  contains the irreducible finite-dimensional subrepresentation
contains the irreducible finite-dimensional subrepresentation 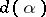 (in the class of polynomials in
(in the class of polynomials in 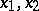 ), the factors of which are totally irreducible. If
), the factors of which are totally irreducible. If 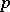 and
and 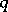 are negative integers,
are negative integers, 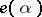 has a dual structure. In all other cases the module
has a dual structure. In all other cases the module 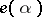 is totally irreducible. In such a case
is totally irreducible. In such a case 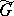 is in one-to-one correspondence with the set of pairs
is in one-to-one correspondence with the set of pairs 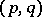 , where
, where 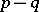 is an integer, factorized with respect to the relation
is an integer, factorized with respect to the relation 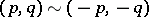 . The subset
. The subset 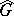 consists of the representations of the basis series (
consists of the representations of the basis series (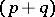 is purely imaginary) (cf. Series of representations), the complementary series
is purely imaginary) (cf. Series of representations), the complementary series 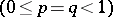 and the trivial (unique) representation
and the trivial (unique) representation 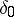 , which results if
, which results if 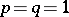 . Let
. Let 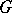 be a semi-simple connected complex Lie group, let
be a semi-simple connected complex Lie group, let 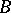 be its maximal solvable (Borel) subgroup, let
be its maximal solvable (Borel) subgroup, let 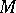 be a maximal torus, let
be a maximal torus, let 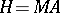 be a Cartan subgroup, and let
be a Cartan subgroup, and let 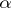 be a character of the group
be a character of the group 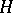 (extended to
(extended to 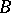 ). Then
). Then 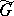 is in one-to-one correspondence with
is in one-to-one correspondence with 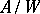 , where
, where 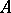 is the set of all characters
is the set of all characters 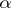 and
and 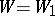 is the Weyl group of the complex algebra
is the Weyl group of the complex algebra 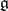 [7]. For characters in "general position" the representation
[7]. For characters in "general position" the representation 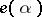 is totally irreducible. The description of the set
is totally irreducible. The description of the set 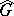 is reduced to the study of the positive definiteness of certain bilinear forms, but the ultimate description is as yet (1988) unknown. Of special interest to real groups are the so-called discrete series (of representations) (direct sums in
is reduced to the study of the positive definiteness of certain bilinear forms, but the ultimate description is as yet (1988) unknown. Of special interest to real groups are the so-called discrete series (of representations) (direct sums in 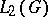 ). All irreducible representations of the discrete series are classified [3] by describing the characters of these representations.
). All irreducible representations of the discrete series are classified [3] by describing the characters of these representations.
For nilpotent connected Lie groups [8] the set 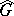 is equivalent to
is equivalent to 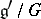 , where
, where 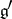 is the linear space dual to
is the linear space dual to 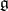 , and the action of
, and the action of 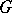 in
in 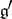 is conjugate with the adjoint representation on
is conjugate with the adjoint representation on 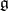 [9]. The correspondence is established by the orbit method [8]. A subalgebra
[9]. The correspondence is established by the orbit method [8]. A subalgebra 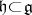 is called the polarization of an element
is called the polarization of an element 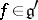 if
if 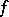 annihilates
annihilates 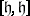 and if
and if
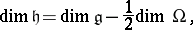 |
where  is the orbit of
is the orbit of 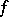 with respect to
with respect to 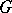 (all orbits are even-dimensional). If
(all orbits are even-dimensional). If 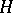 is the corresponding analytic subgroup in
is the corresponding analytic subgroup in 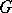 and
and 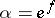 is a character of
is a character of 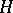 , the representation
, the representation 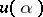 corresponding to
corresponding to 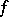 is induced by
is induced by 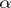 . Here,
. Here, 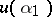 is equivalent to
is equivalent to 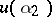 if and only if the corresponding functionals
if and only if the corresponding functionals 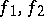 lie on the same orbit
lie on the same orbit  . In the simple case of the group
. In the simple case of the group 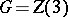 of all unipotent matrices with respect to a fixed basis in
of all unipotent matrices with respect to a fixed basis in 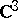 , the orbits of general position in
, the orbits of general position in 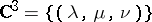 are the two-dimensional planes
are the two-dimensional planes 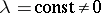 and the points
and the points 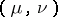 in the plane
in the plane 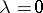 . To each orbit in general position corresponds an irreducible representation
. To each orbit in general position corresponds an irreducible representation 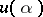 of the group
of the group 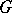 , determined by the formula
, determined by the formula
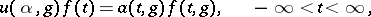 |
in the Hilbert space 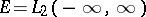 . The infinitesimal operators of this representation coincide with the operators
. The infinitesimal operators of this representation coincide with the operators 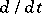 ,
, 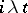 ,
, 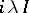 , where
, where 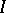 is the identity operator on
is the identity operator on 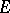 . This result is equivalent to the Stone–von Neumann theorem on self-adjoint operators
. This result is equivalent to the Stone–von Neumann theorem on self-adjoint operators 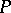 ,
, 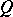 with the commutator relationship
with the commutator relationship 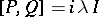 . To each point
. To each point 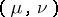 corresponds a one-dimensional representation (a character) of
corresponds a one-dimensional representation (a character) of 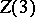 . The set
. The set 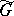 is then described in an analogous way, with values of the parameters
is then described in an analogous way, with values of the parameters 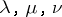 in the complex domain. This method of orbits can be naturally generalized to solvable connected Lie groups and even to arbitrary Lie groups; in the general case the orbits to be considered are orbits in
in the complex domain. This method of orbits can be naturally generalized to solvable connected Lie groups and even to arbitrary Lie groups; in the general case the orbits to be considered are orbits in 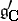 (where
(where 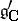 is the complexification of
is the complexification of 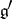 ), which satisfy certain integer conditions [8].
), which satisfy certain integer conditions [8].
The study of the general case is reduced, to a certain extent, to the two cases considered above by means of the theory of induced representations [5], which permits one to describe the irreducible unitary representations of a semi-direct product 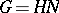 with normal subgroup
with normal subgroup 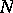 in terms of irreducible representations of
in terms of irreducible representations of 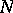 and of certain subgroups of the group
and of certain subgroups of the group 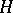 (in view of the Levi–Mal'tsev theorem, cf. Levi–Mal'tsev decomposition). In practice, this method is only effective if the radical is commutative. Another method for studying
(in view of the Levi–Mal'tsev theorem, cf. Levi–Mal'tsev decomposition). In practice, this method is only effective if the radical is commutative. Another method for studying 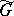 (and also
(and also 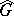 ) is the description of the characters of the irreducible unitary representations of
) is the description of the characters of the irreducible unitary representations of 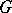 ; the set of such characters is in one-to-one correspondence with
; the set of such characters is in one-to-one correspondence with 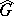 . The validity of the general formula for characters, proposed by A.A. Kirillov [8], has been verified (1988) only for a few special classes of Lie groups.
. The validity of the general formula for characters, proposed by A.A. Kirillov [8], has been verified (1988) only for a few special classes of Lie groups.
Harmonic analysis of functions on 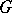 .
.
For a compact Lie group, the harmonic analysis is reduced to the expansion of functions 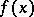 ,
, 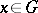 , into generalized Fourier series by the matrix entries of the group
, into generalized Fourier series by the matrix entries of the group 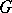 (the Peter–Weyl theorem for
(the Peter–Weyl theorem for 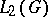 and its analogues for other function classes). For non-compact Lie groups the foundations of harmonic analysis were laid in [1] by the introduction of the generalized Fourier transform
and its analogues for other function classes). For non-compact Lie groups the foundations of harmonic analysis were laid in [1] by the introduction of the generalized Fourier transform
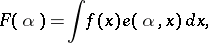 |
where 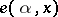 is the operator of the elementary representation
is the operator of the elementary representation 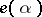 and
and 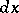 is the Haar measure on
is the Haar measure on 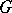 , and by the introduction of the inversion formula (in analogy to the Plancherel formula) for
, and by the introduction of the inversion formula (in analogy to the Plancherel formula) for 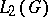 for the case of classical matrix groups
for the case of classical matrix groups 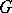 . This result was generalized to locally compact unimodular groups (the abstract Plancherel theorem). The Fourier transform converts convolution of functions on the group to multiplication of their (operator) Fourier images
. This result was generalized to locally compact unimodular groups (the abstract Plancherel theorem). The Fourier transform converts convolution of functions on the group to multiplication of their (operator) Fourier images 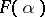 and is accordingly a very important tool in the study of group algebras. If
and is accordingly a very important tool in the study of group algebras. If 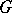 is a semi-simple Lie group, the operators
is a semi-simple Lie group, the operators 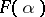 satisfy structure relations of the form
satisfy structure relations of the form
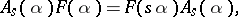 |
 ,
, 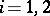 , where
, where 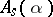 are intertwining operators,
are intertwining operators, 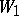 is the Weyl group of the symmetric space
is the Weyl group of the symmetric space 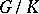 (
(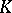 is a maximal compact subgroup in
is a maximal compact subgroup in 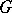 ), and
), and 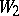 is the Weyl group of the algebra
is the Weyl group of the algebra 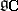 , where
, where 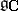 is the complexification of the Lie algebra of the group
is the complexification of the Lie algebra of the group 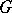 . If the functions
. If the functions 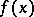 have compact support, the operator functions
have compact support, the operator functions 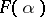 are entire functions of the complex parameter
are entire functions of the complex parameter 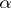 . For the group algebras
. For the group algebras 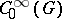 ,
, 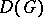 , where
, where 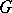 is a semi-simple connected complex Lie group, analogues of the classical Paley–Wiener theorem [7] are known; these are descriptions of the images of these algebras under Fourier transformation. These results permit one to study the structure of a group algebra, its ideals and representations; in particular, they are used in the classification of irreducible representations of a group
is a semi-simple connected complex Lie group, analogues of the classical Paley–Wiener theorem [7] are known; these are descriptions of the images of these algebras under Fourier transformation. These results permit one to study the structure of a group algebra, its ideals and representations; in particular, they are used in the classification of irreducible representations of a group 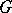 . Analogues of the Paley–Wiener theorem are also known for certain nilpotent (metabelian) Lie groups and for groups of motions of a Euclidean space.
. Analogues of the Paley–Wiener theorem are also known for certain nilpotent (metabelian) Lie groups and for groups of motions of a Euclidean space.
Problems of spectral analysis.
For unitary representations of Lie groups a general procedure is known for the decomposition of the representation into a direct integral of irreducible representations [5]. The problem consists of finding analytical methods which would realize this decomposition for specific classes of groups and their representations, and in the establishment of uniqueness criteria of such a decomposition. For nilpotent Lie groups a method is known for the restriction of an irreducible representation 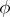 of a group
of a group 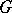 to a subgroup
to a subgroup 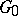 (cf. Orbit method). For non-unitary representations, the task itself must be formulated more precisely, since the property of total reducibility lacks in the class of such representations. In several cases, not the group
(cf. Orbit method). For non-unitary representations, the task itself must be formulated more precisely, since the property of total reducibility lacks in the class of such representations. In several cases, not the group 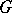 itself is considered, but rather one of its group algebras
itself is considered, but rather one of its group algebras 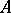 , and the problem of spectral analysis is treated as the study of two-sided ideals of the algebra
, and the problem of spectral analysis is treated as the study of two-sided ideals of the algebra 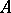 . The problem of spectral analysis (and spectral synthesis) is also closely connected with the problem of approximation of functions on the group
. The problem of spectral analysis (and spectral synthesis) is also closely connected with the problem of approximation of functions on the group 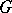 or on the homogeneous space
or on the homogeneous space 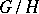 , where
, where 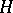 is a subgroup, by linear combinations of matrix entries of the group
is a subgroup, by linear combinations of matrix entries of the group 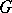 .
.
Applications to mathematical physics.
Cartan was the first to note the connection between the theory of representations of Lie groups and the special functions of mathematical physics. It was subsequently established that the principal classes of functions are closely connected with the representations of classical matrix groups [10]. In fact, the existence of this connection throws light on fundamental problems in the theory of special functions: the properties of completeness and orthogonality, differential and recurrence relations, addition theorems, etc., and also makes it possible to detect new relationships and classes of functions. All these functions are matrix entries of classical groups or their modifications (characters, spherical functions). The theory of expansion with respect to these functions forms part of the general harmonic analysis on a homogeneous space 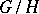 . The fundamental role played by the theory of Lie groups in mathematical physics, particularly in quantum mechanics and quantum field theory, is due to the presence of a group of symmetries (at least approximately) in the fundamental equations of this theory. Classical examples of such symmetries include Einstein's relativity principle (with respect to the Lorentz group), the connection between Mendeleev's table and the representations of the rotation group, the theory of isotopic spin, unitary symmetry of elementary particles, etc. The connection with theoretical physics had a stimulating effect on the development of the general theory of representations of Lie groups.
. The fundamental role played by the theory of Lie groups in mathematical physics, particularly in quantum mechanics and quantum field theory, is due to the presence of a group of symmetries (at least approximately) in the fundamental equations of this theory. Classical examples of such symmetries include Einstein's relativity principle (with respect to the Lorentz group), the connection between Mendeleev's table and the representations of the rotation group, the theory of isotopic spin, unitary symmetry of elementary particles, etc. The connection with theoretical physics had a stimulating effect on the development of the general theory of representations of Lie groups.
References
| [1] | I.M. Gel'fand, M.A. Naimark, "Unitäre Darstellungen der klassischen Gruppen" , Akademie Verlag (1957) (Translated from Russian) |
| [2] | N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French) |
| [3] | A. Borel, "Repŕesentations de groupes localement compacts" , Springer (1972) |
| [4] | E. Nelson, "Analytic vectors" Ann. of Math. , 70 (1959) pp. 572–615 |
| [5] | G.W. Mackey, "Infinite-dimensional group representations" Bull. Amer. Math. Soc. , 69 (1963) pp. 628–686 |
| [6] | M.A. Naimark, "Infinite-dimensional representations of groups and related problems" Itogi Nauk. Ser. Mat. : 2 (1964) pp. 38–82 (In Russian) |
| [7] | D.P. Zhelobenko, "Harmonic analysis of functions on semi-simple complex Lie groups" , Moscow (1974) (In Russian) |
| [8] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [9] | G. Warner, "Harmonic analysis on semi-simple Lie groups" , 1 , Springer (1972) |
| [10] | N.Ya. Vilenkin, "Special functions and the theory of group representations" , Amer. Math. Soc. (1968) (Translated from Russian) |
Comments
The notions of a differentiable or analytic representation are commonly related to the strong topology [9].
The algebra 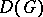 (of generalized functions on
(of generalized functions on 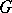 with compact support) is usually denoted by
with compact support) is usually denoted by 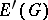 in the West. The notation
in the West. The notation 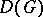 , if used, is then a synonym for
, if used, is then a synonym for 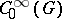 .
.
Recently (1986), 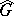 has been determined for
has been determined for  , where
, where 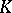 is the field of real or complex numbers or the skew-field of quaternions (D.A. Vogan), for
is the field of real or complex numbers or the skew-field of quaternions (D.A. Vogan), for 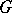 a complex simple Lie group of real rank 2 (M. Duflo) and for
a complex simple Lie group of real rank 2 (M. Duflo) and for 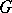 a split-rank or semi-simple real Lie group (Baldoni–Silva–Barbasch). For a survey of the current state-of-affairs see [a3], [a5].
a split-rank or semi-simple real Lie group (Baldoni–Silva–Barbasch). For a survey of the current state-of-affairs see [a3], [a5].
An analogue of the Paley–Wiener theorem is also known for real reductive Lie groups (cf. [a7], [a10]).
References
| [a1] | J. Dixmier, " algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
| [a2] | Harish-Chandra, "Collected papers" , 1–4 , Springer (1984) |
| [a3] | D.A. Vogan, "Representations of real reductive Lie groups" , Birkhäuser (1981) |
| [a4] | W. Casselman, D. Miličić, "Asymptotic behaviour of matrix coefficients of admissible representations" Duke. Math. J. , 49 (1982) pp. 869–930 |
| [a5] | A.W. Knapp, B. Speh, "Status of classification of irreducible unitary representations" F. Ricci (ed.) G. Weiss (ed.) , Harmonic analysis , Lect. notes in math. , 908 , Springer (1982) pp. 1–38 |
| [a6] | M. Duflo, "Construction de représentations unitaires d'un groupe de Lie" , Harmonic analysis and group representations , C.I.M.E. & Liguousi (1982) |
| [a7] | J. Arthur, "A Paley–Wiener theorem for real reductive groups" Acta. Math. , 150 (1983) pp. 1–89 |
| [a8] | W. Rossman, "Kirillov's character formula for reductive Lie groups" Invent. Math. , 48 (1978) pp. 207–220 |
| [a9] | M. Duflo, G. Heckman, M. Vergne, "Projection d'orbites, formule de Kirillov et formule de Blattner" Mém. Soc. Math. France Nouvelle Série , 15 (1985) pp. 65–128 |
| [a10] | P. Delorme, "Théorème de type Paley–Wiener pour les groupes de Lie semi-simple réels avec une seule classe de conjugaison de sous-groupes de Cartan" J. Funct. Anal. , 47 (1982) pp. 26–63 |
Infinite-dimensional representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Infinite-dimensional_representation&oldid=19057