Index theory
The area of mathematics whose main object of study is the index of operators (cf. also Index of an operator; Index formulas).
The main question in index theory is to provide index formulas for classes of Fredholm operators (cf. also Fredholm operator), but this is not the only interesting question. First of all, to be able to provide index formulas, one has to specify what meaning of "index" is agreed upon, then one has to specify to what classes of operators these formulas will apply, and, finally, one has to explain how to use these formulas in applications.
A consequence of this is that index theory also studies various generalizations of the concept of Fredholm index, including $K$-theoretical and cyclic homology indices, for example. Moreover, the study of the analytic properties necessary for the index to be defined are an important part of index theory. Here one includes the study of conditions for being Fredholm or non-Fredholm for classes of operators that nevertheless have finite-dimensional kernels. Soon after (1970s), other invariants of elliptic operators have been defined that are similar in nature to the analytic index. The study of these related invariants is also commonly considered to be part of index theory. The most prominent of these new, related invariants are the Ray–Singer analytic torsion and the eta-invariant. Fixed-point formulas are also usually considered part of index theory, see [a9]. Finally, one of the most important goals of index theory is to study applications of the index theorems to geometry, physics, group representations, analysis, and other fields. There is a very long and fast growing list of papers dealing with these applications.
Index theory has become a subject on its own only after M.F. Atiyah and I. Singer published their index theorems in the sequence of papers [a4], [a6], [a7] (cf. also Index formulas). These theorems had become possible only due to progress in the related fields of $K$-theory [a10], [a5] and pseudo-differential operators (cf. also Pseudo-differential operator) [a35], [a37], [a46]. Important particular cases of the Atiyah–Singer index theorems were known before. Among them, Hirzebruch's signature theorem (cf. also Signature) occupies a special place (see [a33], especially for topics such as multiplicative genera and the Langlands formula for the dimension of spaces of automorphic forms). Hirzebruch's theorem was generalized by A. Grothendieck (see [a22]), who introduced many of the ideas that proved to be fundamental for the proof of the index theorems. All these theorems turned out to be consequences of the Atiyah–Singer index theorems (see also Index formulas for some index formulas that preceded the Atiyah–Singer index formula).
Atiyah–Singer index formulas.
A common characteristic of the first three main index formulas of Atiyah–Singer and Atiyah–Segal is that they depend only on the principal symbol of the operator whose index they compute. (For a differential operator, the principal symbol is given by the terms involving only the highest-order differentials and is independent of the choice of a coordinate system; cf. also Principal part of a differential operator; Symbol of an operator.) The main theorems mentioned above are:
the index theorem for a single elliptic operator $P$ acting between sections of vector bundles on a smooth, compact manifold $M$ (Atiyah–Singer, [a4]);
the equivariant index theorem for a single elliptic operator equivariant with respect to a compact group $G$ (Atiyah–Segal, [a5]); and
the index theorem for families $( P _ { b } ) _ { b \in B }$ of elliptic operators acting on the fibres of a fibre bundle $Y \rightarrow B$ (Atiyah–Singer, [a7]). These results are briefly reviewed below.
A single elliptic operator acting between sections of vector bundles.
If $P$ is an elliptic differential, or, more generally, an elliptic pseudo-differential operator acting between sections of two smooth vector bundles (cf. also Elliptic operator), then $P$ defines a continuous operator between suitable Sobolev spaces with closed range and finite-dimensional kernel and cokernel, that is, a Fredholm operator. The first of the index theorems gives an explicit formula for the Fredholm, or analytic, index $\operatorname{ind} ( P )$ of $P$:
\begin{equation*} \operatorname{ind} ( P ) : = \operatorname { dim } ( \operatorname{ker} ( P ) ) - \operatorname { dim } ( \operatorname { coker } ( P ) ). \end{equation*}
Denote by $\mathcal{T} ( M )$ the Todd class of the complexification of the tangent bundle $T M$ of $M$. If $P$ is an elliptic operator as above, its principal symbol $a = \sigma ( P )$ defines a $K$-theory class $[ a ]$ with compact supports on $T ^ { * } M$ whose Chern character, denoted $\operatorname{Ch} ( [ a ] )$, is in the even cohomology of $T ^ { * } M$ with compact supports. The Atiyah–Singer index formula of [a6] then states that
\begin{equation*} \operatorname{ind} ( P ) = ( - 1 ) ^ { n } \operatorname{Ch} ( [ a ] ) {\cal T} ( M ) [ T ^ { * } M ], \end{equation*}
$n$ being the dimension of the manifold $M$ and $[ T ^ { * } M ]$ being the fundamental class of $T ^ { * } M$. (The factor $( - 1 ) ^ { n }$ reflects the choice of the orientation of $T ^ { * } M$ in the original articles. Other choices for this orientation will lead to different signs.) In other words, the index is obtained by evaluating the compactly supported cohomology class $\operatorname{Ch} ( [ a ] ) \mathcal{T} ( M )$ on the fundamental class of $T ^ { * } M$.
Equivariant index theorem.
The second of the index formulas refines the index when the operator $P$ above is invariant with respect to a compact Lie group, see [a5], [a6]. Recall that the representation ring of a compact group $G$ is defined as the ring of formal linear combinations with integer coefficients of equivalence classes of irreducible representations of $G$ (cf. also Irreducible representation). For operators $P$ equivariant with respect to a compact group $G$, the kernel and cokernel are representations of $G$, so their difference can now be regarded as an element of $R ( G )$, called the equivariant index of $P$. The Atiyah–Singer index formula in [a6] gives the value $\text{ind}_{ g } ( P )$ of the (character of the) index of $P$ at $g \in G$ in terms of invariants of $M ^ { g }$, the set of fixed points of $g$ in $M$. Denote by $a | _ { T ^{*} M ^{ g }}$ the restriction of $a$ to the cotangent bundle of $M ^ { g }$ and by $\mathcal{T} ( M ^ { g } )$ the Todd class of the complexification of the cotangent bundle of $M ^ { g }$. In addition to these ingredients, which are similar to the ingredients appearing in the formula for $\operatorname{ind} ( P )$ above, the formula for $\text{ind}_{ g } ( P )$ involves also a Lefschetz-type contribution, denoted below by $L ( N , g )$, obtained from the action of $g$ on the normal bundle to the set $M ^ { g }$:
\begin{equation*} \operatorname { ind } _ { g } ( P ) = ( - 1 ) ^ { n } \operatorname { Ch } ( [ a | _ { T ^ { * } M ^ { g } } ] ) \mathcal{T} ( M ^ { g } ) L ( N , g ) [ T ^ { * } M ^ { g } ]. \end{equation*}
Families of elliptic operators.
For families of elliptic operators acting on the fibres of a fibre bundle $\pi : Y \rightarrow B$ (cf. also Fibration), a first problem is to make sense of the index. The solution proposed by Atiyah and Singer in [a7] is to define the index as an element of a $K$-theory group, namely $K ^ { 0 } ( B )$ in this case (cf. also $K$-theory). This fortunate choice has opened the way for many other developments in index theory. Actually, in the two index theorems mentioned above, the index can also be interpreted using a $K$-theory group, the $K$-theory of the algebra $\mathbf{C}$ of complex numbers in the first index theorem and the $K$-theory group of $C ^ { * } ( G )$, the norm closure of the convolution algebra of $G$, in the equivariant index theorem. For the Chern character of the family index of a family of elliptic operators $( P _ { b } )$ as above, there is a formula similar to the formula for the index of a single elliptic operator. The principal symbols $a _ { b } = \sigma ( P _ { b } )$ of the operators $P _ { b }$ define, in this case, a class $[ a ]$ in the $K$-theory with compact supports of $T _ { \text{vert} } ^ { * } Y : = T ^ { * } Y / \pi ^ { * } ( T ^ { * } B )$, the vertical cotangent bundle to the fibres of $\pi : Y \rightarrow B$, as in the case of a single elliptic operator. Denote by $\mathcal{T} ( M | B )$ the Todd class of the complexification of $T _ { \text { vert } } ^ { * } Y$ and by $\pi_{ *} : H _ { c } ^ { * } ( T _ { \text { vert } } ^ { * } Y ) \rightarrow H ^ { * - 2 n} ( B )$ the morphism induced by integration along the fibres, with $n$ being the common dimension of the fibres of $\pi$. Then
\begin{equation*} \operatorname{Ch} ( \operatorname{ ind } ( P ) ) = ( - 1 ) ^ { n } \pi_{ *} ( \operatorname { ind } ( [ a ] ) {\cal T} ( M | B ) ). \end{equation*}
This completes the discussion of these three main theorems of Atiyah and Singer.
$K$-theory in index theory.
The role of $K$-theory in the proof and applications of the index theorems can hardly be overstated and certainly does not stop at providing an interpretation of the index as an element of a $K$-theory group. A far-reaching consequence of the use of $K$-theory, which depends on Bott periodicity (or more precisely, the Thom isomorphism, cf. also Bott periodicity theorem), is that all elliptic operators can be connected, by a homotopy of Fredholm operators, to certain operators of a very particular kind, the so-called generalized Dirac operators (see below). It is thus sufficient to prove the index theorems for generalized Dirac operators.
Due to their differential-geometric properties, it is possible to give more concrete proofs of the Atiyah–Singer index theorem for generalized Dirac operators, using heat kernels, for example (cf. also Heat content asymptotics). The generalized Dirac operator with coefficients in the spin bundle is called simply the Dirac operator (sometimes called the Atiyah–Singer operator). See below for more about generalized Dirac operators.
Applications of index theorems.
After the publication of the first papers by Atiyah and Singer, index theory has evolved into essentially three directions:
a direction which consists of applications and new proofs of the index theorems (especially "local" proofs using heat kernels);
a direction which studies invariants other than the index; and
a direction which aims at more general index theorems. There is a very large number of applications of index theorems to topology and other areas of mathematics. A few examples follow. In [a12], Atiyah and W. Schmid used Atiyah's $L^{2}$-index theorem for coverings [a11] to construct discrete series representations. In [a34], N.J. Hitchin used the families index theorem to prove that there exist metrics whose associated Dirac operators have non-trivial kernels (in suitable dimensions). An index theorem for foliations that is close in spirit to Atiyah's $L^{2}$-index theorem was obtained by A. Connes [a27].
The index of Dirac (or Atiyah–Singer) operators was used to formulate and then prove the Gromov–Lawson conjecture [a32], which states that a compact, spin, simply connected manifold of dimension $\geq 5$ admits a metric of positive scalar curvature if and only if the index of the spin Dirac operator (in an appropriate $K$-theory group) is zero. This conjecture was proved by S. Stolz, [a48]. Dirac operators have been used to give a concrete construction of $K$-homology [a16].
Some of the applications of the index theorems require new proofs of these theorems, usually relying on the "heat-kernel method" . The main idea of this method is as follows. H. McKean and Singer [a39] stated the problem of investigating the behaviour, as $t \rightarrow 0$, $t > 0$, of the (super-trace of the) heat kernel. More precisely, let
\begin{equation*} k _ { t } ( x , y ) = \operatorname { str } ( e ^ { - t D ^ { 2 } } ) = \operatorname { tr } ( e ^ { - t D _ { + } ^ { * } D _ { + } } ) - \operatorname { tr } ( e ^ { - t D _ { + } D _ { + } ^ { * } } ) \end{equation*}
be the well-known term appearing in the McKean–Singer index formula, where $D = D _ { + } + D _ { + } ^ { * }$ is a self-adjoint geometric operator (cf. also Self-adjoint operator) with $D _ { + }$ mapping the subspace of even sections to the subspace of odd sections. They considered the case of the de Rham operator $D _ { + } + D _ { + } ^ { * }$, where $D _ { + }$ is then the de Rham differential (cf. also de Rham cohomology). It was known that the integral over the whole manifold of $k _ { t } ( x , x )$ gives the analytic index of $D _ { + }$, and they expressed the hope that $k _ { t } ( x , x )$ will have a definite limit as $t \rightarrow 0$. This was proved for various particular cases by V. Patodi in [a54] and then by P. Gilkey [a29], [a30] using invariant theory (see [a31] for an exposition of this method). This method was finally refined in [a1] to give a clear and elegant proof of the local index theorem for all Dirac operators.
Inspired by a talk of Atiyah, J.-M. Bismut investigated connections between probability theory and index theory. He was able to use the stochastic calculus (cf. also Malliavin calculus) to give a new proof of the local index theorem [a17]. His methods then generalized to give proofs of the local index theorem for families of Dirac operators [a18] using Quillen's theory of super-connections [a43], and of the Atiyah–Bott fixed-point formulas [a19]. An application of his results is the determination of the Quillen metric on the determinant bundle [a21].
The local index theorems have many connections to physics, where Dirac operators play a prominent role. Actually, several physicists have come up with arguments for a proof of the local index theorem based on supersymmetry and functional integration, see [a8] and [a53], for example. Building on these arguments, E. Getzler has obtained a short and elegant proof of the local index theorem [a14], [a31], which also uses supersymmetry. Moreover, ideas inspired from physics have lead E. Witten to conjecture that certain twisted Dirac operators on $S ^ { 1 }$-manifolds have an index that is a trivial representation of $S ^ { 1 }$, see [a52]. This was proved by C.H. Taubes [a49] (see also [a23] and [a51]). For the Dirac operator, this had been proved before by Atiyah and F. Hirzebruch [a2].
Other invariants.
Heat-kernel methods have proved very useful in dealing with non-compact and singular spaces. A common feature of these spaces is that the index formulas for the natural operators on them depend on more than just the principal symbol, which leads to the appearance of non-local invariants in these index formulas. In general, there exists no good understanding, at this time (2000), of what these non-local invariants are, except in particular cases. The most prominent of these particular cases is the Atiyah–Patodi–Singer index theorem for manifolds with boundary. Other results in these directions were obtained in [a25], [a40], [a41], [a47]. In all these cases, eta-invariants of certain boundary operators must be included in the formula for the index. Moreover, one has to either work on complete manifolds or to include boundary conditions to make the given problems Fredholm. The Atiyah–Patodi–Singer index theorem [a3], e.g., requires such boundary conditions; see below.
Let $M$ be a compact manifold with boundary $\partial M$ and metric $g$ which is a product metric in a suitable cylindrical neighbourhood of $\partial M$. Fix a Clifford module $W$ on $M$ (cf. also Clifford algebra) and an admissible connection $\nabla$. Denote by $D : = \sum c ( e _ { i } ) \nabla _ { e_i }$ the generalized Dirac operator on $W$, where $c : T ^ { * } M \cong T M \rightarrow \operatorname { End } ( W )$ is the Clifford multiplication and $e _ { i }$ is a local orthonormal basis (cf. also Orthogonal basis). Also, let $D _ { 0 }$ be the corresponding generalized Dirac operator on $\partial M$, which is (essentially) self-adjoint because $\partial M$ is compact without boundary. Then the eigenvalues of $D _ { 0 }$ will form a discrete subset of the real numbers; denote by $P _ { + }$ the spectral projection corresponding to the eigenvalues of $D _ { 0 }$ that are $\geq 0$. Decompose $D = D _ { + } + D _ { + } ^ { * }$ using the natural ${\bf Z} / 2 {\bf Z}$-grading on $W$. The operator $D _ { + }$, the chiral Dirac operator, acts from sections of $W _ { + }$ to sections of $W_-$, and has an infinite-dimensional kernel. Because of that, Atiyah, Patodi and Singer have introduced a non-local boundary condition of the form $P _ { + } f = 0$, for $f$ a smooth section of $W _ { + }$ over $\partial M$, which is a compact perturbation of the Calderón projection boundary condition. The effect of this boundary condition is that the restriction of $D$ to the subspace of sections satisfying this boundary condition is Fredholm. Assume that $M$ is $\operatorname {spin}^ { c }$ with spinor bundle $S$, such that $W = S \otimes E$, and let $h$ denote the dimension of the kernel of $D _ { 0 }$. The index of the resulting operator $D _ { + }$ with the above boundary conditions is then
\begin{equation*} \operatorname{ind}_{\alpha} ( D _ { + } ) = \int _ { M } \hat { A } ( M ) \operatorname{Ch} ( E ) - \frac { \eta ( D _ { 0 } ) + h } { 2 }. \end{equation*}
This formula was generalized by Bismut and J. Cheeger in [a20] to families of manifolds with boundary, the result being expressed using the "eta form" $\hat{\eta}$. More precisely, using the notation above, they proved that
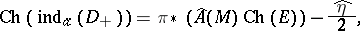 |
provided that all Dirac operator associated to the boundaries of the fibres are invertible.
Presently (2000), cyclic homology (cf. also Cyclic cohomology) is probably the only general tool to deal with index problems in which the index belongs to an abstract, possibly unknown, $K$-theory group, or to deal with index theorems involving non-local invariants. See [a26], [a36], [a38], or [a50] for the basic results on cyclic homology. The relation between the $K$-theory of the algebra $A$ and the cyclic homology of $A$ is via Chern characters $\operatorname{Ch} : K _ { 0 } ( A ) \rightarrow \operatorname{HC} _ { 2 n } ( A )$, $n \geq 0$, and is due to Connes and M. Karoubi.
Generalized index theorems.
In [a24], Connes and H. Moscovici have generalized Atiyah's $L^{2}$-index theorem, which allowed them to obtain a proof of the Novikov conjecture (cf. also $C ^ { * }$-algebra) for certain classes of groups. The index theorem, also called the higher index theorem for coverings, is as follows. Let $\tilde { M } \rightarrow M$ be a covering of a compact manifold $M$ with group of deck transformations $\Gamma$ (cf. also Monodromy transformation). If $D$ is an elliptic differential operator on $M$ invariant with respect to $\Gamma$ (such as the signature operator), then it has an index $\operatorname{ind} ( D ) \in K _ { 0 } ( C _ { r } ^ { * } ( \Gamma ) )$, the $K _ { 0 }$-group of the closure of the group algebra of $\Gamma$ acting on $l ^ { 2 } ( \Gamma )$. This index was defined by A.T. Fomenko and A. Mishchenko in [a28]. This index can be refined to an index in $K_0({\cal R}\otimes {\bf C}[\Gamma])$, where $\mathcal{R}$ is the algebra of infinite matrices with complex entries and with rapid decrease. Using cyclic cohomology and the Chern character in cyclic homology, every cohomology class $\phi \in H ^ { * } ( \Gamma ) = H ^ { * } ( B \Gamma )$ gives rise to a morphism $\phi * : K _ { 0 } ( {\cal R} \otimes {\bf C} [ \Gamma ] ) \rightarrow \bf C$, and the problem is to determine $\phi_{*} ( \text { ind } ( D ) )$. If $\phi = 1 \in H ^ { 0 } ( \Gamma )$, then this number is exactly the von Neumann index appearing in Atiyah's $L^{2}$-index formula.
Let $f : M \rightarrow B \Gamma$ be the mapping that classifies the covering $\tilde { M } \rightarrow M$ and let $\mathcal{T} ( M )$ be the Todd class of the complexification of $T _ { \text { vert } } ^ { * } Y$. If $D$ is an elliptic invariant differential operator, its principal symbol $a = \sigma ( P )$ defines a $K$-theory class $[ a ]$ with compact supports on $T ^ { * } M$, whose Chern character $\operatorname{Ch} ( [ a ] )$ is in the even cohomology of $T ^ { * } M$ with compact supports, as in the case of the Atiyah–Singer index theorem for a single elliptic operator. Suppose $\phi \in H ^ { 2 m } ( \Gamma )$; then the Connes–Moscovici higher index theorem for coverings [a24] states that
\begin{equation*} \phi _ { * } ( \text { ind } ( D ) ) = ( - 1 ) ^ { n } \left( 2 \pi i ) ^ { - m } ( \operatorname {Ch} ( [ a ] ) \mathcal{T} ( M ) f ^ { * } \phi \right) [ T ^ { * } M ]. \end{equation*}
The Chern character in cyclic cohomology turns out to be a natural mapping, and this can be interpreted as a general index theorem in cyclic cohomology [a42]. It is hoped that this general index theorem will help explain the ubiquity of the Todd class in index theorems.
For more information on index theory, see, e.g., [a14], [a15], [a45]. To get a balanced point of view, see also [a13] for an account of the original approach to the Atiyah–Singer index theorems, which also gives all the necessary background a student needs.
References
| [a1] | M. Atiyah, R. Bott, V. Patodi, "On the heat equation and the index theorem" Invent. Math. , 19 (1973) pp. 279–330 (Erata ibid. 28 (1975), 277-280) MR0650828 Zbl 0364.58016 Zbl 0257.58008 |
| [a2] | M. Atiyah, F. Hirzebruch, "Spin manifolds and group actions" , Essays in Topology and Related subjects , Springer (1994) pp. 18–28 MR0278334 Zbl 0193.52401 |
| [a3] | M. Atiyah, V. Patodi, I. Singer, "Spectral asymmetry and Riemannian geometry I" Math. Proc. Cambridge Philos. Soc. , 77 (1975) pp. 43–69 MR0397797 MR0397798 MR0397799 Zbl 0297.58008 |
| [a4] | M. Atiyah, I. Singer, "The index of elliptic operators I" Ann. of Math. , 87 (1968) pp. 484–530 MR0236950 MR0232402 Zbl 0164.24001 |
| [a5] | M. Atiyah, G. Segal, "The index of elliptic operators II" Ann. of Math. , 87 (1968) pp. 531–545 MR0236953 MR0236951 Zbl 0164.24201 |
| [a6] | M. Atiyah, I. Singer, "The index of elliptic operators III" Ann. of Math. , 93 (1968) pp. 546–604 MR0236952 Zbl 0164.24301 |
| [a7] | M. Atiyah, I. Singer, "The index of elliptic operators IV" Ann. of Math. , 93 (1971) pp. 119–138 MR0279833 Zbl 0212.28603 |
| [a8] | L. Alvarez-Gaumé, "Supersymmetry and the Atiyah–Singer index theorem" Comm. Math. Phys. , 90 (1983) pp. 161–173 Zbl 0528.58034 |
| [a9] | M. Atiyah, R. Bott, "A Lefschetz fixed-point formula for elliptic complexes II: Applications." Ann. of Math. , 88 (1968) pp. 451–491 MR0232406 Zbl 0167.21703 |
| [a10] | M. Atiyah, "$K$-theory" , Benjamin (1967) MR0224084 MR0224083 Zbl 0159.53401 Zbl 0159.53302 |
| [a11] | M. Atiyah, "Elliptic operators, discrete subgroups, and von Neumann algebras" Astérisque , 32/33 (1969) pp. 43–72 |
| [a12] | M. Atiyah, W. Schmid, "A geometric construction of the discrete series" Invent. Math. , 42 (1977) pp. 1–62 MR0463358 Zbl 0373.22001 |
| [a13] | B. Booss–Bavnbek, D. Bleecker, "Topology and analysis. The Atiyah–Singer index formula and gauge-theoretic physics" , Universitext , Springer (1985) MR0771117 Zbl 0551.58031 |
| [a14] | N. Berline, E. Getzler, M. Vèrgne, "Heat kernels and Dirac operator" , Grundl. Math. Wissenschaft. , 298 , Springer (1996) MR2273508 MR1215720 |
| [a15] | B. Booss–Bavnbek, K. Wojciechowski, "Elliptic boundary problems for Dirac operators" , Math. Th. Appl. , Birkhäuser (1993) MR1233386 Zbl 0797.58004 |
| [a16] | P. Baum, R. Douglas, "Index theory, bordism, and $K$-homology" , Operator Algebras and $K$-Theory (San Francisco, Calif., 1981) , Contemp. Math. , 10 , Amer. Math. Soc. (1982) pp. 1–31 MR0658506 |
| [a17] | J.-M. Bismut, "The Atiyah–Singer theorems: a probabilistic approach" J. Funct. Anal. , 57 (1984) pp. 56–99 MR0756173 MR0744920 Zbl 0556.58027 Zbl 0538.58033 |
| [a18] | J.-M. Bismut, "The index theorem for families of Dirac operators: two heat equation proofs" Invent. Math. , 83 (1986) pp. 91–151 Zbl 0592.58047 |
| [a19] | J.-M. Bismut, "The Atiyah–Singer theorems: a probabilistic approach. II. The Lefschetz fixed point formulas" J. Funct. Anal. , 57 : 3 (1984) pp. 329–348 MR0744920 MR0756173 Zbl 0556.58027 |
| [a20] | J.-M. Bismut, J. Cheeger, "$ \eta $-invariants and their adiabatic limits" J. Amer. Math. Soc. , 2 (1989) pp. 33–70 MR0966608 Zbl 0671.58037 |
| [a21] | J.-M. Bismut, D. Freed, "The analysis of elliptic families: Metrics and connections on determinant bundles" Comm. Math. Phys. , 106 (1986) pp. 103–163 MR853982 |
| [a22] | A. Borel, J.-P. Serre, "Le téorème de Riemann–Roch (d'apreès Grothendieck)" Bull. Soc. Math. France , 86 (1958) pp. 97–136 |
| [a23] | R. Bott, C. Taubes, "On the rigidity theorems of Witten" J. Amer. Math. Soc. , 2 : 1 (1989) pp. 137–186 MR0954493 Zbl 0667.57009 |
| [a24] | A. Connes, H. Moscovici, "Cyclic cohomology, the Novikov conjecture and hyperbolic groups" Topology , 29 (1990) pp. 345–388 MR1066176 Zbl 0759.58047 |
| [a25] | J. Cheeger, "On the Hodge theory of Riemannian pseudomanifolds" , Geometry of the Laplace operator (Univ. Hawaii, 1979) , Proc. Symp. Pure Math. , XXXVI , Amer. Math. Soc. (1980) pp. 91–146 MR0573430 Zbl 0461.58002 |
| [a26] | A. Connes, "Non-commutative differential geometry" Publ. Math. IHES , 62 (1985) pp. 41–144 MR823176 Zbl 0592.46056 Zbl 0564.58002 |
| [a27] | A. Connes, "Sur la théorie noncommutative de l'intégration" , Algèbres d'Opérateurs , Lecture Notes in Mathematics , 725 , Springer (1982) pp. 19–143 |
| [a28] | A. Miščenko, A. Fomenko, "The index of elliptic operators over $C ^ { * }$-algebras" Izv. Akad. Nauk. SSSR Ser. Mat. , 43 (1979) pp. 831–859 MR548506 |
| [a29] | P. Gilkey, "Curvature and the eigenvalues of the Laplacian for elliptic complexes" Adv. Math. , 10 (1973) pp. 344–382 MR0324731 Zbl 0259.58010 |
| [a30] | P. Gilkey, "Curvature and the eigenvalues of the Dolbeault complex for Kaehler manifolds" Adv. Math. , 11 (1973) pp. 311–325 MR0334290 Zbl 0285.53044 |
| [a31] | P. Gilkey, "Invariance theory, the heat equation, and the Atiyah–Singer index theorem" , CRC (1994) MR1396308 MR0783634 Zbl 0856.58001 Zbl 0565.58035 |
| [a32] | M. Gromov, H. Lawson Jr., "The classification of simply connected manifolds of positive scalar curvature" Ann. of Math. , 111 (1980) pp. 423–434 MR0577131 Zbl 0463.53025 |
| [a33] | F. Hirzebruch, "Topological methods in algebraic geometry" , Grundl. Math. Wissenschaft. , 131 , Springer (1966) (Edition: Third) MR0202713 Zbl 0138.42001 |
| [a34] | N. Hitchin, "Harmonic spinors" Adv. Math. , 14 (1974) pp. 1–55 MR0358873 Zbl 0284.58016 |
| [a35] | L. Hörmander, "Pseudo-differential operators" Commun. Pure Appl. Math. , 18 (1965) pp. 501–517 MR0180740 Zbl 0125.33401 |
| [a36] | M. Karoubi, "Homology cyclique et K-theorie" Astérisque , 149 (1987) pp. 1–147 Zbl 0601.18007 |
| [a37] | J. Kohn, L. Nirenberg, "An algebra of pseudodifferential operators" Commun. Pure Appl. Math. , 18 (1965) pp. 269–305 MR176362 |
| [a38] | J.-L. Loday, D. Quillen, "Cyclic homology and the Lie homology of matrices" Comment. Math. Helv. , 59 (1984) pp. 565–591 MR780077 Zbl 0565.17006 |
| [a39] | H. McKean Jr., I. Singer, "Curvature and the eigenvalues of the Laplacian" J. Diff. Geom. , 1 (1967) pp. 43–69 |
| [a40] | R. Melrose, "The Atiyah–Patodi–Singer index theorem" , Peters (1993) MR1348401 Zbl 0796.58050 |
| [a41] | W. Müller, "Manifolds with cusps of rank one, spectral theory and an $L^{2}$-index theorem" , Lecture Notes in Mathematics , 1244 , Springer (1987) |
| [a42] | V. Nistor, "Higher index theorems and the boundary map in cyclic cohomology" Documenta Math. (1997) pp. 263–296 ((electronic)) MR1480038 Zbl 0893.19002 |
| [a43] | D. Quillen, "Superconnections and the Chern character" Topology , 24 (1985) pp. 89–95 MR0790678 Zbl 0569.58030 |
| [a44] | D. Ray, I. Singer, "$R$-torsion and the laplacian on Riemannian manifolds" Adv. Math. , 7 (1971) pp. 145–210 MR0295381 Zbl 0239.58014 |
| [a45] | J. Roe, "Elliptic operators, topology and asymptotic methods" , Pitman Res. Notes in Math. Ser. , 179 , Longman (1988) MR0960889 Zbl 0654.58031 |
| [a46] | R.T. Seeley, "Refinement of the functional calculus of Calderòn and Zygmund" Indag. Math. , 27 (1965) pp. 521–531 Nederl. Akad. Wetensch. Proc. Ser. A , 68 (1965) MR0226450 Zbl 0141.13302 |
| [a47] | Mark Stern, "$L^{2}$-index theorems on locally symmetric spaces" Invent. Math. , 96 (1989) pp. 231–282 MR0989698 Zbl 0694.58039 |
| [a48] | S. Stolz, "Simply connected manifolds of positive scalar curvature" Ann. of Math. , 136 : 2 (1992) pp. 511–540 MR1189863 Zbl 0784.53029 |
| [a49] | C. Taubes, "$S ^ { 1 }$ actions and elliptic genera" Comm. Math. Phys. , 122 (1989) pp. 455–526 MR0998662 Zbl 0683.58043 |
| [a50] | B.L. Tsygan, "Homology of matrix Lie algebras over rings and Hochschild homology" Uspekhi Mat. Nauk. , 38 (1983) pp. 217–218 MR0695483 Zbl 0526.17006 |
| [a51] | E. Witten, "Supersymmetry and Morse theory" J. Diff. Geom. , 17 (1982) pp. 661–692 MR0683171 Zbl 0499.53056 |
| [a52] | E. Witten, "Elliptic genera and quantum field theory" Comm. Math. Phys. , 109 (1987) pp. 525–536 MR0885560 Zbl 0625.57008 |
| [a53] | E. Witten, "Constraints on supersymmetry breaking" Nucl. Phys. B , 202 (1982) pp. 253–316 MR0668987 |
| [a54] | V. Patodi, "Curvature and the eigenforms of the Laplace operator" J. Diff. Geom. , 5 (1971) pp. 233–249 MR0292114 Zbl 0211.53901 |
Index theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Index_theory&oldid=50758