Group scheme
A generalization of the concept of an algebraic group. Let 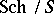 be the category of schemes over a ground scheme
be the category of schemes over a ground scheme 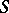 ; a group object of this category is known as a group scheme over the scheme
; a group object of this category is known as a group scheme over the scheme 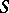 (or a group
(or a group 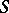 -scheme, or an
-scheme, or an 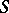 -scheme group). For a group scheme
-scheme group). For a group scheme 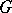 over
over 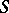 the functor of points
the functor of points 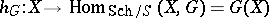 is a contravariant functor from the category
is a contravariant functor from the category 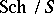 into the category of groups
into the category of groups 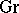 . The category
. The category 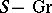 of group schemes over
of group schemes over 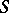 is defined as the complete subcategory of the category of such functors formed by the representable functors (cf. Representable functor).
is defined as the complete subcategory of the category of such functors formed by the representable functors (cf. Representable functor).
Examples.
1) An algebraic group over a field 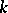 is a reduced group scheme of finite type over
is a reduced group scheme of finite type over 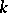 . (A reduced group scheme of finite type over a field is sometimes referred to as an algebraic group.)
. (A reduced group scheme of finite type over a field is sometimes referred to as an algebraic group.)
2) A functor which assigns to an 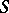 -scheme
-scheme 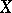 the additive (or multiplicative) group of the ring of sections of the structure sheaf
the additive (or multiplicative) group of the ring of sections of the structure sheaf 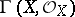 is representable. The corresponding group scheme over
is representable. The corresponding group scheme over 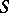 is said to be the additive (or multiplicative) group scheme, and is denoted by
is said to be the additive (or multiplicative) group scheme, and is denoted by 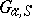 (or
(or 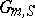 ). For any
). For any 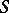 -scheme
-scheme 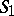 one has
one has
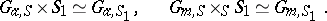 |
3) Each abstract group 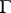 defines a group scheme
defines a group scheme 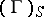 , which is the direct sum of a family of schemes
, which is the direct sum of a family of schemes 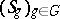 , each one of which is isomorphic to
, each one of which is isomorphic to 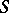 . The corresponding functor maps an
. The corresponding functor maps an 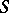 -scheme
-scheme 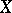 to the direct sum
to the direct sum 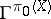 , where
, where 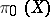 is the set of connected components of
is the set of connected components of 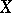 .
.
If 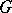 is a group scheme over
is a group scheme over 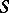 then, for any point
then, for any point 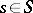 , the fibre
, the fibre 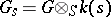 is a group scheme over the residue field
is a group scheme over the residue field 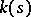 of this point. In particular, any group scheme of finite type over
of this point. In particular, any group scheme of finite type over 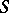 can be regarded as a family of algebraic groups parametrized by the base
can be regarded as a family of algebraic groups parametrized by the base 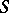 . The terminology of the theory of schemes is extended to group schemes; thus, one speaks of smooth, flat, finite, and singular group schemes.
. The terminology of the theory of schemes is extended to group schemes; thus, one speaks of smooth, flat, finite, and singular group schemes.
For any group scheme 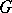 the corresponding reduced scheme
the corresponding reduced scheme 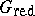 is also a group scheme; the canonical closed imbedding
is also a group scheme; the canonical closed imbedding 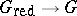 is a morphism of group schemes. Each reduced group scheme of locally finite type over a perfect field is smooth. Each reduced group scheme of locally finite type over a field of characteristic zero is reduced (Cartier's theorem).
is a morphism of group schemes. Each reduced group scheme of locally finite type over a perfect field is smooth. Each reduced group scheme of locally finite type over a field of characteristic zero is reduced (Cartier's theorem).
Many concepts and results in the theory of algebraic groups have their analogues for group schemes. Thus, there exists an analogue of the structure theory of Borel–Chevalley for affine algebraic groups [5], and a cohomology theory of extensions of group schemes and homogeneous spaces over group schemes has been developed [2], [5]. On the other hand, many problems and results specific to the theory of group schemes are connected with the presence of nilpotent elements in the structure sheaf of both the ground scheme and the group scheme itself. Thus, infinitesimal and formal deformations of group schemes [4], problems of lifting into zero characteristic, and formal completion of group schemes (cf. Formal group) have all been studied. Group schemes arise in a natural manner in the study of algebraic groups over a field of positive characteristic (cf.  -divisible group).
-divisible group).
The concept of an affine group scheme over an affine ground scheme 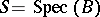 is dual to the concept of a commutative Hopf algebra; this is the case if
is dual to the concept of a commutative Hopf algebra; this is the case if 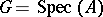 is a group scheme for which
is a group scheme for which 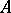 is a commutative Hopf algebra.
is a commutative Hopf algebra.
See also Commutative group scheme; Finite group scheme.
References
| [1] | J. Tate, F. Oort, "Group schemes of prime order" Ann. Sc. Ecole Norm. Sup. , 3 (1970) pp. 1–21 |
| [2] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , Masson (1970) |
| [3] | F. Oort, "Commutative group schemes" , Lect. notes in math. , 15 , Springer (1966) |
| [4] | F. Oort, "Finite group schemes, local moduli for abelian varieties and lifting problems" Compos. Math. , 23 (1971) pp. 256–296 |
| [5] | M. Demazure, A. Grothendieck, "Schémas en groupes I-III" , Lect. notes in math. , 151–153 , Springer (1970) |
Comments
Other examples of group schemes are Abelian (group) varieties.
References
| [a1] | D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974) |
Group scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Group_scheme&oldid=18884