Green function
A function related to integral representations of solutions of boundary value problems for differential equations.
The Green function of a boundary value problem for a linear differential equation is the fundamental solution of this equation satisfying homogeneous boundary conditions. The Green function is the kernel of the integral operator inverse to the differential operator generated by the given differential equation and the homogeneous boundary conditions (cf. Kernel of an integral operator). The Green function yields solutions of the inhomogeneous equation satisfying the homogeneous boundary conditions. Finding the Green function reduces the study of the properties of the differential operator to the study of similar properties of the corresponding integral operator.
Green function for ordinary differential equations.
Let 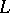 be the differential operator generated by the differential polynomial
be the differential operator generated by the differential polynomial
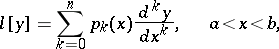 |
and the boundary conditions 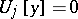 ,
, 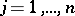 , where
, where
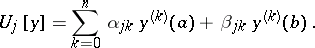 |
The Green function of  is the function
is the function  that satisfies the following conditions:
that satisfies the following conditions:
1)  is continuous and has continuous derivatives with respect to
is continuous and has continuous derivatives with respect to  up to order
up to order 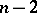 for all values of
for all values of  and
and 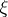 in the interval
in the interval 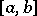 .
.
2) For any given 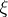 in
in 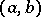 the function
the function 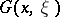 has uniformly-continuous derivatives of order
has uniformly-continuous derivatives of order  with respect to
with respect to  in each of the half-intervals
in each of the half-intervals 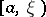 and
and 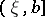 and the derivative of order
and the derivative of order 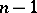 satisfies the condition
satisfies the condition
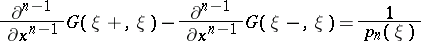 |
if 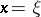 .
.
3) In each of the half-intervals 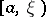 and
and 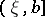 the function
the function 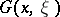 , regarded as a function of
, regarded as a function of  , satisfies the equation
, satisfies the equation 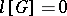 and the boundary conditions
and the boundary conditions 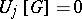 ,
, 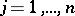 .
.
If the boundary value problem 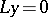 has trivial solutions only, then
has trivial solutions only, then 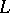 has one and only one Green function [1]. For any continuous function
has one and only one Green function [1]. For any continuous function  on
on 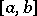 there exists a solution of the boundary value problem
there exists a solution of the boundary value problem 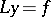 , and it can be expressed by the formula
, and it can be expressed by the formula
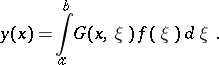 |
If the operator 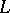 has a Green function
has a Green function 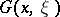 , then the adjoint operator
, then the adjoint operator 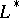 also has a Green function, equal to
also has a Green function, equal to 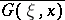 . In particular, if
. In particular, if 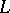 is self-adjoint (
is self-adjoint (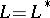 ), then
), then 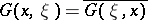 , i.e. the Green function is a Hermitian kernel in this case. Thus, the Green function of the self-adjoint second-order operator
, i.e. the Green function is a Hermitian kernel in this case. Thus, the Green function of the self-adjoint second-order operator 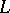 generated by the differential operator with real coefficients
generated by the differential operator with real coefficients
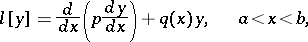 |
and the boundary conditions 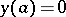 ,
, 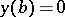 has the form:
has the form:
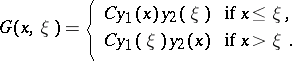 |
Here 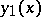 and
and 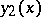 are arbitrary independent solutions of the equation
are arbitrary independent solutions of the equation 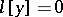 satisfying, respectively, the conditions
satisfying, respectively, the conditions 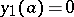 ,
, 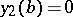 ;
;  , where
, where 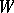 is the Wronski determinant (Wronskian) of
is the Wronski determinant (Wronskian) of 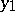 and
and 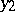 . It can be shown that
. It can be shown that 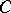 is independent of
is independent of 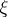 .
.
If the operator 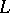 has a Green function, then the boundary eigen value problem
has a Green function, then the boundary eigen value problem 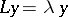 is equivalent to the integral equation
is equivalent to the integral equation 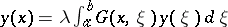 , to which Fredholm's theory is applicable (cf. also Fredholm theorems). For this reason the boundary value problem
, to which Fredholm's theory is applicable (cf. also Fredholm theorems). For this reason the boundary value problem 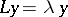 can have at most a countable number of eigen values
can have at most a countable number of eigen values 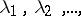 without finite limit points. The conjugate problem has complex-conjugate eigen values of the same multiplicity. For each
without finite limit points. The conjugate problem has complex-conjugate eigen values of the same multiplicity. For each 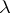 that is not an eigen value of
that is not an eigen value of 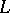 it is possible to construct the Green function
it is possible to construct the Green function 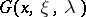 of the operator
of the operator 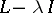 , where
, where 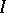 is the identity operator. The function
is the identity operator. The function 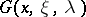 is a meromorphic function of the parameter
is a meromorphic function of the parameter 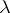 ; its poles can be eigen values of
; its poles can be eigen values of 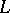 only. If the multiplicity of the eigen value
only. If the multiplicity of the eigen value 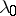 is one, then
is one, then
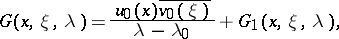 |
where 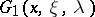 is regular in a neighbourhood of the point
is regular in a neighbourhood of the point 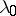 , and
, and 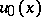 and
and 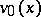 are the eigen functions of
are the eigen functions of 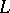 and
and 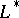 corresponding to the eigen values
corresponding to the eigen values 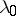 and
and 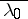 and normalized so that
and normalized so that
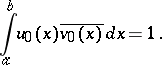 |
If 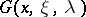 has infinitely-many poles and if these are of the first order only, then there exists a complete biorthogonal system
has infinitely-many poles and if these are of the first order only, then there exists a complete biorthogonal system
 |
of eigen functions of 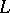 and
and 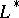 . If the eigen values are numbered in increasing sequence of their absolute values, then the integral
. If the eigen values are numbered in increasing sequence of their absolute values, then the integral
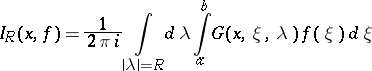 |
is equal to the partial sum
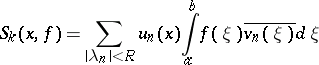 |
of the expansion of 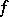 with respect to the eigen functions of
with respect to the eigen functions of 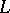 . The positive number
. The positive number 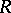 is so selected that the function
is so selected that the function 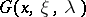 is regular in
is regular in 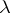 on the circle
on the circle  . For a regular boundary value problem and for any piecewise-smooth function
. For a regular boundary value problem and for any piecewise-smooth function  in the interval
in the interval 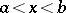 , the equation
, the equation
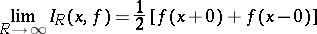 |
is valid, that is, an expansion into a convergent series is possible [1].
If the Green function 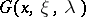 of the operator
of the operator 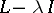 has multiple poles, then its principal part is expressed by canonical systems of eigen and adjoint functions of the operators
has multiple poles, then its principal part is expressed by canonical systems of eigen and adjoint functions of the operators 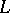 and
and 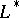 [2].
[2].
In the case considered above, the boundary value problem 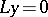 has no non-trivial solutions. If, on the other hand, such non-trivial solutions exist, a so-called generalized Green function is introduced. Let there exist, e.g., exactly
has no non-trivial solutions. If, on the other hand, such non-trivial solutions exist, a so-called generalized Green function is introduced. Let there exist, e.g., exactly 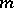 linearly independent solutions of the problem
linearly independent solutions of the problem 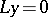 . Then a generalized Green function
. Then a generalized Green function 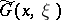 exists that has properties 1) and 2) of an ordinary Green function, satisfies the boundary conditions as a function of
exists that has properties 1) and 2) of an ordinary Green function, satisfies the boundary conditions as a function of  if
if 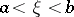 and, in addition, is a solution of the equation
and, in addition, is a solution of the equation
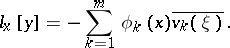 |
Here 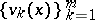 is a system of linearly independent solutions of the adjoint problem
is a system of linearly independent solutions of the adjoint problem 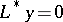 , while
, while 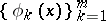 is an arbitrary system of continuous functions biorthogonal to it. Then
is an arbitrary system of continuous functions biorthogonal to it. Then
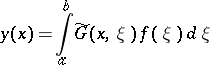 |
is the solution of the boundary value problem 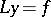 if the function
if the function 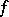 is continuous and satisfies the solvability criterion, i.e. is orthogonal to all
is continuous and satisfies the solvability criterion, i.e. is orthogonal to all 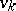 .
.
If 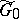 is one of the generalized Green functions of
is one of the generalized Green functions of 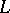 , then any other generalized Green function can be represented in the form
, then any other generalized Green function can be represented in the form
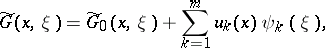 |
where 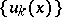 is a complete system of linearly independent solutions of the problem
is a complete system of linearly independent solutions of the problem 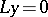 , and
, and  are arbitrary continuous functions [3].
are arbitrary continuous functions [3].
Green function for partial differential equations.
1) Elliptic equations. Let 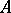 be the elliptic differential operator of order
be the elliptic differential operator of order 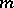 generated by the differential polynomial
generated by the differential polynomial
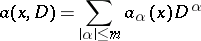 |
in a bounded domain 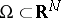 and the homogeneous boundary conditions
and the homogeneous boundary conditions 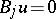 , where
, where 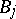 are boundary operators with coefficients defined on the boundary
are boundary operators with coefficients defined on the boundary 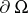 of
of  , which is assumed to be sufficiently smooth. A function
, which is assumed to be sufficiently smooth. A function 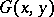 is said to be a Green function for
is said to be a Green function for 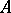 if, for any fixed
if, for any fixed  , it satisfies the homogeneous boundary conditions
, it satisfies the homogeneous boundary conditions 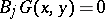 and if, regarded as a generalized function, it satisfies the equation
and if, regarded as a generalized function, it satisfies the equation
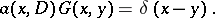 |
In the case of operators with smooth coefficients and normal boundary conditions, which ensure that the solution of the homogeneous boundary value problem is unique, a Green function exists and the solution of the boundary value problem 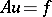 can be represented in the form (cf. [4])
can be represented in the form (cf. [4])
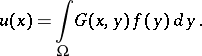 |
In such a case the uniform estimates for 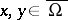 ,
,
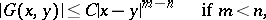 |
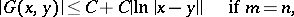 |
are valid for the Green function, and the latter is uniformly bounded if 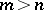 .
.
The boundary eigen value problem 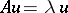 is equivalent to the integral equation
is equivalent to the integral equation
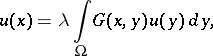 |
to which Fredholm's theory (cf. [5]) is applicable (cf. Fredholm theorems). Here, the Green function of the adjoint boundary value problem is 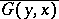 . It follows, in particular, that the number of eigen values is at most countable, and there are no finite limit points; the adjoint boundary value problem has complex-conjugate eigen values of the same multiplicity.
. It follows, in particular, that the number of eigen values is at most countable, and there are no finite limit points; the adjoint boundary value problem has complex-conjugate eigen values of the same multiplicity.
A Green function has been more thoroughly studied for second-order equations, since the nature of the singularity of the fundamental solution can be explicitly written out. Thus, for the Laplace operator the Green function has the form
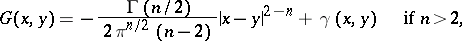 |
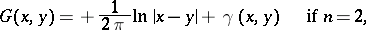 |
where 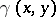 is a harmonic function in
is a harmonic function in  chosen so that the Green function satisfies the boundary condition.
chosen so that the Green function satisfies the boundary condition.
The Green function 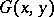 of the first boundary value problem for a second-order elliptic operator
of the first boundary value problem for a second-order elliptic operator 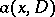 with smooth coefficients in a domain
with smooth coefficients in a domain  with Lyapunov-type boundary
with Lyapunov-type boundary 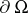 , makes it possible to express the solution of the problem
, makes it possible to express the solution of the problem
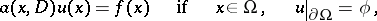 |
in the form
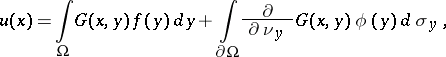 |
where 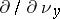 is the derivative along the outward co-normal of the operator
is the derivative along the outward co-normal of the operator 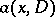 and
and 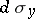 is the surface element on
is the surface element on 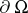 .
.
If the homogeneous boundary condition 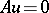 has non-trivial solutions, a generalized Green function is introduced, just as for ordinary differential equations. Thus, a generalized Green function, the so-called Neumann function [3], is available for the Laplace operator.
has non-trivial solutions, a generalized Green function is introduced, just as for ordinary differential equations. Thus, a generalized Green function, the so-called Neumann function [3], is available for the Laplace operator.
2) Parabolic equations. Let 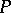 be the parabolic differential operator of order
be the parabolic differential operator of order 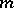 generated by the differential polynomial
generated by the differential polynomial
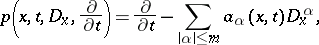 |
 |
and the homogeneous initial and boundary conditions
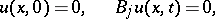 |
where 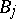 are boundary operators with coefficients defined for
are boundary operators with coefficients defined for 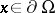 and
and 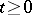 . The Green function of the operator
. The Green function of the operator 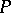 is a function
is a function 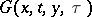 which for arbitrary fixed
which for arbitrary fixed 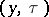 with
with 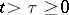 and
and 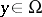 satisfies the homogeneous boundary conditions
satisfies the homogeneous boundary conditions 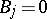 and also satisfies the equation
and also satisfies the equation
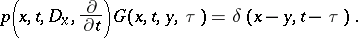 |
For operators with smooth coefficients and normal boundary conditions, which ensures the uniqueness of the solution of the problem 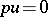 , a Green function exists, and the solution of the equation
, a Green function exists, and the solution of the equation
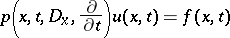 |
satisfying the homogeneous boundary conditions and the initial conditions 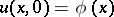 , has the form
, has the form
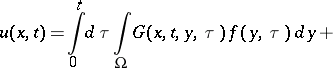 |
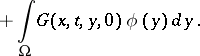 |
In the study of elliptic or parabolic systems the Green function is replaced by the concept of a Green matrix, by means of which solutions of boundary value problems with homogeneous boundary conditions for these systems are expressed as integrals of the products of a Green matrix by the vectors of the right-hand sides and the initial conditions [7].
Green functions are named after G. Green (1828), who was the first to study a special case of such functions in his studies on potential theory.
References
| [1] | M.A. Naimark, "Lineare Differentialoperatoren" , Akademie Verlag (1960) (Translated from Russian) |
| [2] | M.V. Keldysh, "On the characteristic values and characteristic functions of certain classes of non-self-adjoint equations" Dokl. Akad. Nauk. SSSR , 77 : 1 (1951) pp. 11–14 (In Russian) |
| [3] | V.V. Sobolev, "Course in theoretical astrophysics" , NASA , Washington, D.C. (1969) (Translated from Russian) |
| [4] | L. Bers, F. John, M. Schechter, "Partial differential equations" , Interscience (1964) |
| [5] | L. Gårding, "Dirichlet's problem for linear elliptic partial differential equations" Math. Scand. , 1 : 1 (1953) pp. 55–72 |
| [6] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) |
| [7] | S.D. Eidel'man, "Parabolic systems" , North-Holland (1969) (Translated from Russian) |
Comments
References
| [a1] | J.K. Hale, "Ordinary differential equations" , Wiley (1980) |
| [a2] | P.R. Garabedian, "Partial differential equations" , Wiley (1964) |
Green function in function theory.
In the theory of functions of a complex variable, a (real) Green function is understood to mean a Green function for the first boundary value problem for the Laplace operator, i.e. a function of the type
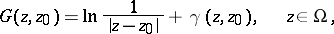 | (1) |
where 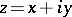 is the complex variable,
is the complex variable, 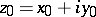 is the pole of the Green function,
is the pole of the Green function, 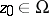 , and
, and 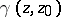 is a harmonic function of
is a harmonic function of  which takes the values
which takes the values 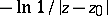 at the boundary
at the boundary 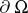 . Let the domain
. Let the domain  be simply-connected and let
be simply-connected and let 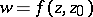 be the analytic function which realizes the conformal mapping of
be the analytic function which realizes the conformal mapping of  onto the unit disc so that
onto the unit disc so that 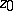 maps to the centre of the disc, and such that
maps to the centre of the disc, and such that 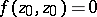 ,
, 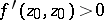 .
.
Then
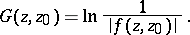 | (2) |
If 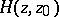 is the harmonic function conjugate with
is the harmonic function conjugate with 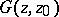 ,
, 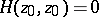 , then the analytic function
, then the analytic function 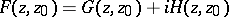 is said to be a complex Green function of
is said to be a complex Green function of  with pole
with pole 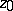 . The inversion of formula (2) yields
. The inversion of formula (2) yields
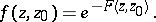 | (3) |
Formulas (2) and (3) show that the problems of constructing a conformal mapping of  into the disc and of finding a Green function are equivalent. The Green functions
into the disc and of finding a Green function are equivalent. The Green functions 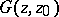 ,
, 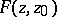 are invariant under conformal mappings, which may sometimes facilitate their identification (see Mapping method).
are invariant under conformal mappings, which may sometimes facilitate their identification (see Mapping method).
In the theory of Riemann surfaces it is more convenient to define Green functions with the aid of a minimum property, valid for a function (1): Of all functions 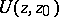 on a Riemann surface
on a Riemann surface  that are positive and harmonic for
that are positive and harmonic for 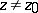 and have in a neighbourhood of
and have in a neighbourhood of 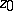 the form
the form
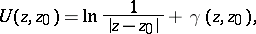 | (4) |
where 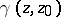 is a harmonic function which is regular on the entire surface
is a harmonic function which is regular on the entire surface  , the Green function, if it exists, is the least, i.e.
, the Green function, if it exists, is the least, i.e. 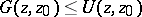 . Here, the existence of a Green function is typical for Riemann surfaces of hyperbolic type. If a Green function is thus defined, it no longer vanishes, generally speaking, anywhere on the (ideal) boundary of the Riemann surface. The situation is similar in potential theory (see also Potential theory, abstract). For an arbitrary open set
. Here, the existence of a Green function is typical for Riemann surfaces of hyperbolic type. If a Green function is thus defined, it no longer vanishes, generally speaking, anywhere on the (ideal) boundary of the Riemann surface. The situation is similar in potential theory (see also Potential theory, abstract). For an arbitrary open set  , e.g. in the Euclidean space
, e.g. in the Euclidean space 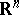 ,
, 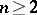 , the Green function
, the Green function 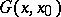 can also be defined with the aid of the minimum property discussed above, but for
can also be defined with the aid of the minimum property discussed above, but for 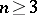 the expression
the expression 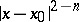 should be substituted for
should be substituted for 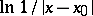 in formula (4). In general, such a Green function does not necessarily tend to zero as the boundary
in formula (4). In general, such a Green function does not necessarily tend to zero as the boundary 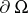 is approached. A Green function does not exist for Riemann surfaces of parabolic type or for certain domains in
is approached. A Green function does not exist for Riemann surfaces of parabolic type or for certain domains in 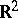 (e.g. for
(e.g. for 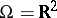 ).
).
References
| [1] | S. Stoilov, "The theory of functions of a complex variable" , 1–2 , Moscow (1962) (In Russian; translated from Rumanian) |
| [2] | R. Nevanlinna, "Uniformisierung" , Springer (1953) |
| [3] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) |
E.D. Solomentsev
Comments
See also [a1] and [a3] for Green functions in classical potential theory, and [a2] for Green functions in axiomatic potential theory.
In the theory of functions of several complex variables, more specifically in pluri-potential theory (cf. also Potential theory), Green functions for the complex Monge–Ampère equation have been introduced. Ideally such a Green function should be a fundamental solution for the complex Monge–Ampère operator 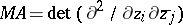 , with boundary values
, with boundary values  and in addition plurisubharmonic (cf. also Plurisubharmonic function). It is only possible to achieve a fair analogy of the classical one-dimensional theory for pseudo-convex domains (cf. Pseudo-convex and pseudo-concave). Several inequivalent definitions of Green function have been proposed. One of these is as follows. Let
and in addition plurisubharmonic (cf. also Plurisubharmonic function). It is only possible to achieve a fair analogy of the classical one-dimensional theory for pseudo-convex domains (cf. Pseudo-convex and pseudo-concave). Several inequivalent definitions of Green function have been proposed. One of these is as follows. Let  be a domain in
be a domain in 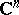 ,
, 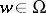 . Let
. Let 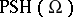 denote the plurisubharmonic functions (cf. Plurisubharmonic function) on
denote the plurisubharmonic functions (cf. Plurisubharmonic function) on  . The Green function for
. The Green function for  with pole at
with pole at 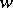 is
is
 |
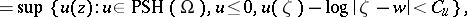 |
where 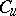 is a constant depending on
is a constant depending on  . Thus, for every fixed
. Thus, for every fixed 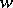 ,
, 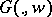 is plurisubharmonic. For
is plurisubharmonic. For 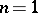 ,
, 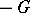 equals the usual Green function. Of course one wants
equals the usual Green function. Of course one wants 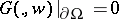 and also
and also 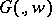 a continuous function to
a continuous function to 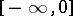 , but this is equivalent to
, but this is equivalent to  being a hyper-convex domain (that is, a pseudo-convex domain that admits a continuous, bounded plurisubharmonic exhaustion function). If this is the case, one also has:
being a hyper-convex domain (that is, a pseudo-convex domain that admits a continuous, bounded plurisubharmonic exhaustion function). If this is the case, one also has:
1) 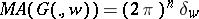 , where
, where 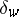 is Dirac measure at
is Dirac measure at 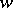 ,
,
2) 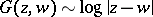 as
as 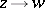 and
and 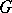 is continuous on
is continuous on 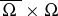 .
.
If  is strictly convex, then
is strictly convex, then  is symmetric:
is symmetric: 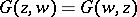 and
and 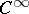 on
on 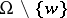 . If
. If  is only strictly pseudo-convex, then
is only strictly pseudo-convex, then 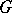 need not be symmetric and not even
need not be symmetric and not even 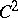 . One can introduce a kind of Green function in which the symmetry is incorporated, see [a5], but one may loose 1) and 2). For
. One can introduce a kind of Green function in which the symmetry is incorporated, see [a5], but one may loose 1) and 2). For  strictly pseudo-convex the following inequality holds (L. Lempert):
strictly pseudo-convex the following inequality holds (L. Lempert):
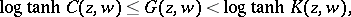 |
with equality for convex domains. Here 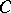 and
and 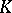 denote the Carathéodory and the Kobayashi distance, respectively.
denote the Carathéodory and the Kobayashi distance, respectively.
If 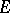 is a bounded set in
is a bounded set in 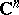 , the Green function with pole at
, the Green function with pole at 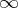 for
for 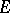 is
is
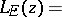 |
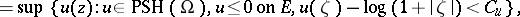 |
and analogous to the one-variable case there is a Robin function
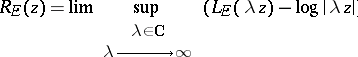 |
and a logarithmic capacity
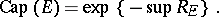 |
For general sets 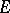 ,
, 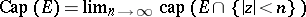 . This capacity has the property that the sets of capacity zero are precisely the pluri-polar sets.
. This capacity has the property that the sets of capacity zero are precisely the pluri-polar sets.
References
| [a1] | L.L. Helms, "Introduction to potential theory" , Wiley (Interscience) (1969) |
| [a2] | K. Janssen, "On the existence of a Green function for harmonic spaces" Math. Annalen , 208 (1974) pp. 295–303 |
| [a3] | N.S. [N.S. Landkov] Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian) |
| [a4] | E. Bedford, "Survey of pluri-potential theory" (forthcoming) |
| [a5] | U. Cegrell, "Capacities in complex analysis" , Vieweg (1988) |
| [a6] | J.P. Demailly, "Mesures de Monge–Ampère et mesures pluriharmoniques" Math. Z. , 194 (1987) pp. 519–564 |
Green's function in statistical mechanics.
A time-ordered linear combination of correlation functions (cf. Correlation function in statistical mechanics), which is a convenient intermediate quantity in computations of interacting particles.
Green's function in statistical quantum mechanics.
Two-time commutator temperature Green functions are the most often used: retarded 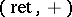 , advanced
, advanced 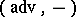 and causal (c). These are defined by the relations:
and causal (c). These are defined by the relations:
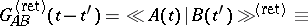 |
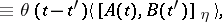 |
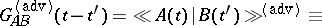 |
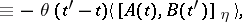 |
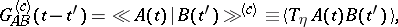 |
where
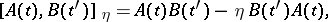 |
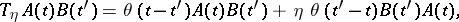 |
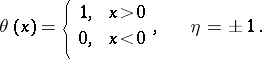 |
Here, 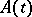 and
and 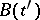 are time-dependent dynamic variables (operators on the state space of the system in the Heisenberg representation);
are time-dependent dynamic variables (operators on the state space of the system in the Heisenberg representation); 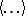 denotes the average over the Gibbs statistical aggregate; the value of
denotes the average over the Gibbs statistical aggregate; the value of 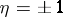 is selected for the sake of convenience. The effectiveness of the use of Green's functions depends to a large extent on the use of spectral representations of their Fourier transforms
is selected for the sake of convenience. The effectiveness of the use of Green's functions depends to a large extent on the use of spectral representations of their Fourier transforms 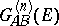 ,
, 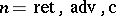 . Thus, for non-zero temperature the following representation is valid for the advanced and retarded Green functions:
. Thus, for non-zero temperature the following representation is valid for the advanced and retarded Green functions:
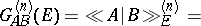 |
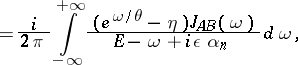 |
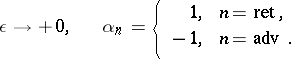 |
Here 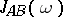 is the spectral density,
is the spectral density, 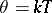 , where
, where 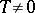 is the absolute temperature, and
is the absolute temperature, and 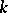 is the Boltzmann constant. In the unit system employed,
is the Boltzmann constant. In the unit system employed, 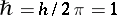 where
where 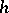 is the Planck constant. In particular, the following formula is valid:
is the Planck constant. In particular, the following formula is valid:
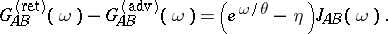 |
This formula makes it possible to compute the spectral density (and thus also a number of physical characteristics of the system) by way of a Green's function. Similar spectral formulas also exist for zero temperature. The singularities (poles in the complex plane) of the Fourier transform of a Green function characterize the spectrum and the damping of the elementary perturbations in the system. The principal sources for the computation of a Green function include: a) the approximate solution of an infinite chain of interlacing equations, which is derived directly from the definition of the Green's function by "splitting" the chain on the basis of physical ideas; b) the summation of the physical "fundamental" terms of the series of perturbation theory (summation of diagrams); this method is mainly used in computing causal Green functions and it resembles in many ways the method for the computation of a Green function in quantum field theory.
Green's function in classical statistical mechanics
are two-time retarded (ret) and advanced (adv) Green's functions obtained by replacing the operators 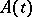 and
and 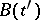 in the appropriate quantum formulas established for the quantum case (for
in the appropriate quantum formulas established for the quantum case (for 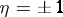 ) by the dynamic state functions of the classical system under study, and replacing the commutator
) by the dynamic state functions of the classical system under study, and replacing the commutator 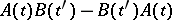 (the quantum Poisson brackets) by the classical (ordinary) Poisson brackets;
(the quantum Poisson brackets) by the classical (ordinary) Poisson brackets; 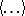 denotes, correspondingly, averaging over Gibbs' classical aggregate. The introduction of a causal Green's function has no meaning here, since the product of the dynamic variables is commutative. In analogy with the quantum case, spectral representations of the Fourier transform of a Green's function exist and can be effectively employed. The principal source for the computation of a classical Green function is the system of equations obtained by infinitesimally varying the Hamiltonian of some system of equations for the correlation functions: the Bogolyubov chain of equations, a system of hydrodynamic equations, etc.
denotes, correspondingly, averaging over Gibbs' classical aggregate. The introduction of a causal Green's function has no meaning here, since the product of the dynamic variables is commutative. In analogy with the quantum case, spectral representations of the Fourier transform of a Green's function exist and can be effectively employed. The principal source for the computation of a classical Green function is the system of equations obtained by infinitesimally varying the Hamiltonian of some system of equations for the correlation functions: the Bogolyubov chain of equations, a system of hydrodynamic equations, etc.
References
| [1] | N.N. Bogolyubov, S.V. Tyablikov, "Retarded and advanced Green functions in statistical physics" Soviet Phys. Dokl. , 4 (1960) pp. 589–593 Dokl. Akad. Nauk SSSR , 126 (1959) pp. 53 |
| [2] | D.N. Zubarev, "Double-time Green functions in statistical physics" Soviet Phys. Uspekhi , 3 (1960) pp. 320–345 Uspekhi Fiz. Nauk , 71 (1960) pp. 71–116 |
| [3] | N.N. Bogolyubov, jr., B.I. Sadovnikov, Zh. Eksperim. Teor. Fiz. , 43 : 8 (1962) pp. 677 |
| [4] | N.N. Bogolyubov jr., B.I. Sadovnikov, "Some questions in statistical mechanics" , Moscow (1975) (In Russian) |
| [5] | , Statistical physics and quantum field theory , Moscow (1973) (In Russian) |
V.N. Plechko
Comments
In the special but frequently used case where 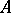 and
and 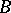 are field operators, or creation operators and annihilation operators, one chooses
are field operators, or creation operators and annihilation operators, one chooses 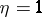 for bosons and
for bosons and 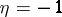 for fermions.
for fermions.
Green function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Green_function&oldid=16518