Golay code
From a purely mathematical point of view, the Golay codes are the most interesting codes constructed as yet (1996). The binary Golay code  is a
is a  -dimensional subspace of
-dimensional subspace of  with the property that any two vectors (i.e., words) differ in at least
with the property that any two vectors (i.e., words) differ in at least  positions (they have distance
positions (they have distance  ). In coding terminology,
). In coding terminology,  is a
is a  binary code, i.e., a
binary code, i.e., a  -error-correcting code (cf. Error-correcting code). Similarly, the ternary Golay code
-error-correcting code (cf. Error-correcting code). Similarly, the ternary Golay code  is a
is a 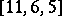 ternary code. It was shown by A. Tietäväinen and J.H. van Lint (see [a3]) that the Golay codes are the only non-trivial
ternary code. It was shown by A. Tietäväinen and J.H. van Lint (see [a3]) that the Golay codes are the only non-trivial  -error-correcting perfect codes with
-error-correcting perfect codes with 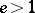 over any alphabet
over any alphabet  for which
for which 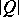 is a prime power. A perfect
is a prime power. A perfect  -error-correcting code is a subset of
-error-correcting code is a subset of 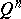 such that every vector in the space has distance at most
such that every vector in the space has distance at most  to a unique codeword.
to a unique codeword.
An extension of a code 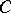 of length
of length  is the set of words of length
is the set of words of length  obtained by adjoining an extra coordinate to all the words of
obtained by adjoining an extra coordinate to all the words of 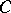 in such a way that the sum of the
in such a way that the sum of the  coordinates is
coordinates is  . The extended codes
. The extended codes  and
and  are of interest in group theory because their automorphism groups are the
are of interest in group theory because their automorphism groups are the  -transitive Mathieu groups
-transitive Mathieu groups  and
and 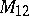 (cf. also Mathieu group).
(cf. also Mathieu group).
For design theory (cf. also Design with mutually orthogonal resolutions; Block design), the Golay codes are important for the following reason. The words of weight (i.e., number of non-zero coordinates) 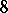 in
in  are the blocks of the (unique) Steiner system
are the blocks of the (unique) Steiner system  . Similarly, the words of weight
. Similarly, the words of weight  in
in 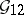 support the blocks of the (unique) Steiner system
support the blocks of the (unique) Steiner system 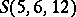 .
.
For each of the codes, several constructions are known. E.g.,
1) Make a list of the numbers 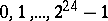 written binary as vectors in
written binary as vectors in 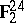 . Delete each vector that has distance less than
. Delete each vector that has distance less than 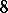 to a previous vector that has not been deleted. At the end of this procedure,
to a previous vector that has not been deleted. At the end of this procedure,  vectors will remain. They form a linear code, in fact
vectors will remain. They form a linear code, in fact 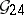 .
.
2) In the spaces 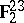 and
and 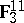 , consider the codes of length
, consider the codes of length 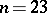 , respectively
, respectively  , generated by the vectors
, generated by the vectors 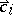 (
( ) for which
) for which  if
if 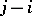 is a non-zero square and
is a non-zero square and  otherwise. One thus obtains the binary and the ternary Golay code.
otherwise. One thus obtains the binary and the ternary Golay code.
3) Consider the 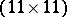 -circulant matrix with top row
-circulant matrix with top row  . This is the incidence matrix of the unique
. This is the incidence matrix of the unique  -
- 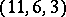 -design. Form
-design. Form 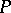 by bordering this matrix with a column of
by bordering this matrix with a column of 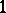 's in front and a row of
's in front and a row of 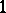 's on top, with a
's on top, with a  in the upper left-hand corner (cf. Bordering method). Then adjoin
in the upper left-hand corner (cf. Bordering method). Then adjoin 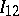 in front of
in front of 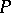 . One obtains a
. One obtains a  -matrix
-matrix  in which every row has eight
in which every row has eight  's (except the top row, which has
's (except the top row, which has 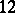 ). The rows of
). The rows of 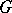 generate
generate 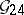 .
.
4) As in 3), form a 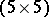 -circulant with top row
-circulant with top row 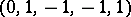 and border it on top with a row of
and border it on top with a row of  's. To this, adjoin
's. To this, adjoin  in front to form a
in front to form a 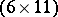 -matrix
-matrix 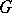 . The rows of
. The rows of  generate the
generate the  ternary Golay code.
ternary Golay code.
For other constructions and more theory of these codes, see the references.
M.J.E. Golay (1902– 1989) was a Swiss physicist who worked in many different fields. He is known for his work on infrared spectroscopy and the invention of the capillary column, but to mathematicians mainly for his discovery of the two Golay codes.
References
| [a1] | A.E. Brouwer, "Block designs" R. Graham (ed.) M. Grötschel (ed.) L. Lovász (ed.) , Handbook of Combinatorics , Elsevier (1995) pp. Chapt. 14 |
| [a2] | P.J. Cameron, J.H. van Lint, "Designs, graphs, codes and their links" , Cambridge Univ. Press (1991) |
| [a3] | J.H. van Lint, "Introduction to coding theory" , Springer (1992) |
| [a4] | J.H. van Lint, R.M. Wilson, "A course in combinatorics" , Cambridge Univ. Press (1992) |
| [a5] | F.J. MacWilliams, N.J.A. Sloane, "The theory of error-correcting codes" , North-Holland (1977) |
Golay code. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Golay_code&oldid=13633