Generalized function algebras
Let $\Omega$ be an open subset of ${\bf R} ^ { n }$. A generalized function algebra is an associative, commutative differential algebra $\mathcal{A} ( \Omega )$ containing the space of distributions $\mathcal{D} ^ { \prime } ( \Omega )$ or other distribution spaces as a linear subspace (cf. also Generalized functions, space of). An early construction of a non-associative, non-commutative algebra was given by H. König [a6]. The main current (2000) direction has been to construct associative, commutative algebras as reduced powers $\nu ^ { \Lambda } / \mathcal{I}$ of classical function spaces $\mathcal{V}$. A further approach uses analytic continuation and asymptotic series of distributions.
To describe the principles, consider the space $\mathcal{V} = \mathcal{C} ^ { \infty } ( \Omega )$ of infinitely differentiable functions on $\Omega$ (cf. also Differentiable function). Let $\Lambda$ be an infinite index set, $\mathcal{B}$ a differential subalgebra of $\mathcal{V} ^ { \Lambda }$ and $\cal I$ a differential ideal in $\mathcal{B}$. The generalized function algebra $\mathcal{A} ( \Omega )$ is defined as the factor algebra $\mathcal{A} ( \Omega ) = \mathcal{B} / \mathcal{I}$. Assuming that $\Lambda$ is a directed set, let $( \varphi _ { \lambda } ) _ { \lambda \in \Lambda }$ be a net in $\mathcal{C} ^ { \infty } ( \mathbf{R} ^ { n } )$ (cf. also Net (directed set)) converging to the Dirac measure in $\mathcal{D} ^ { \prime } ( \mathbf{R} ^ { n } )$ (cf. also Generalized functions, space of). Any compactly supported distribution $w \in \mathcal{E} ^ { \prime } ( \Omega )$ can be imbedded in $\mathcal{V} ^ { \Lambda }$ by convolution (cf. also Generalized function): $w \mapsto ( w ^ { * } \varphi _ { \lambda } ) _ { \lambda \in \Lambda }$. Appropriate conditions on $\mathcal{B}$ and $\cal I$ will guarantee that this extends to an imbedding of ${\cal E} ^ { \prime } ( \Omega )$ into $\mathcal{A} ( \Omega )$. An imbedding of $\mathcal{D} ^ { \prime } ( \Omega )$ is obtained, provided the family $\{ \mathcal{A} ( \Omega ) : \Omega \text { open } \}$ forms a sheaf of differential algebras on ${\bf R} ^ { n }$ (the restriction mappings are defined componentwise on representatives). This imbedding preserves the derivatives of distributions. It follows from the impossibility result of L. Schwartz (see Multiplication of distributions) that it cannot retain the pointwise product of continuous functions at the same time. If $\cal I$ is contained in the subspace $\mathcal Z$ of $\mathcal{V} ^ { \Lambda }$ comprised by those nets which converge weakly to zero, then an equivalence relation $u \sim v$ can be defined on $\mathcal{A} ( \Omega )$ by requiring that $( u _ { \lambda } - v _ { \lambda } ) _ { \lambda \in \Lambda } \in \mathcal{Z}$ for representatives $( u _ { \lambda } ) _ { \lambda \in \Lambda }$ and $( v _ { \lambda } ) _ { \lambda \in \Lambda }$ of $u$ and $v$. The pointwise product of continuous functions (as well as all products obtained by multiplication of distributions) are retained up to this equivalence relation. A list of typical examples of generalized function algebras follows:
1) $\mathcal{B} = ( \mathcal{C} ^ { \infty } ( \Omega ) ) ^ { \mathbf{N} }$, ${\cal I} _ { 0 } = \{ ( u _ { j } ) _ { j \in \bf N }$: there is $j _0$ such that $u _ { j } \equiv 0$ for $j \geq j_0 \}$. The algebra $\mathcal{A} ( \Omega ) = \mathcal{B} / \mathcal{I} _ { 0 }$ was introduced by C. Schmieden and D. Laugwitz [a10] in their foundations of infinitesimal analysis.
2) Let $\mathcal U$ be a free ultrafilter on the infinite set $\Lambda$ and define ${\cal I _ { U } }= \{ ( u _ { \lambda } ) _ { \lambda \in \Lambda }$: the set of indices $\{ \lambda : u _ { \lambda } \equiv 0 \}$ belongs to ${\cal U} \}$, let $\mathcal{B} = ( \mathcal{C} ^ { \infty } ( \Omega ) ) ^ { \Lambda }$. Then $\square ^ { * } \mathcal{C} ^ { \infty } ( \Omega ) = \mathcal{B} / \mathcal{I}_{ \mathcal{U}}$ is an instance of the ultrapower construction of the algebra of internal smooth functions of non-standard analysis (A. Robinson [a8]).
Neither 1) nor 2) provide sheaves on ${\bf R} ^ { n }$. To get a sheaf, localization must be introduced:
3) Let $\mathcal{B} = ( \mathcal{C} ^ { \infty } ( \Omega ) ) ^ { \mathbf{N} }$, ${\cal I} _ { 0 , \operatorname{loc} } = \{ ( u _ { j } ) _ { j \in \bf N }$: for each compact subset $K \subset \Omega$ there is a $j _0$ such that $u _ { j } | _ { K } \equiv 0$ for $j \geq j_0 \}$. The algebra $\mathcal{A}( \Omega ) = \mathcal{B} / \mathcal{I}_{ 0 , \operatorname { loc }}$ was introduced by Yu.V. Egorov [a3] (cf. also Egorov generalized function algebra).
4) Let $\mathcal{E} _ { M } = \{ ( u _ { \varepsilon } ) _ { \varepsilon > 0 } \in \mathcal{C} ^ { \infty } ( \Omega ) ^ { ( 0 , \infty ) }$: for each compact subset $K \subset \Omega$ and each multi-index $\alpha \in {\bf N} _ { 0 } ^ { n }$ there is an $N > 0$ such that the supremum of $| \partial ^ { \alpha } u _ { \varepsilon } ( x ) |$ over $x \in K$ is of order $O ( \varepsilon ^ { - N } )$ as $\varepsilon \rightarrow 0 \}$. Let $\mathcal{N} = \{ ( u _ { \varepsilon } ) _ { \varepsilon > 0 } \in \mathcal{E} _ { M }$: for each compact subset $K \subset \Omega$, each multi-index $\alpha \in {\bf N} _ { 0 } ^ { n }$ and each $q \geq 0$, the supremum of $| \partial ^ { \alpha } u _ { \varepsilon } ( x ) |$ over $x \in K$ is of order $O ( \varepsilon ^ { q } )$ as $\varepsilon \rightarrow 0 \}$. Then $\mathcal{G} ( \Omega ) = \mathcal{E} _ { M } / \mathcal{N}$ is one of the versions of the algebras of J.F. Colombeau [a1] (cf. also Colombeau generalized function algebras). It is distinguished by the fact that the imbedding of $\mathcal{D} ^ { \prime } ( \Omega )$ gives $\mathcal{C} ^ { \infty } ( \Omega )$ as a faithful subalgebra.
5) Let $\mathcal{B} = ( \mathcal{C} ^ { \infty } ( \Omega ) ) ^ { \mathbf{N} }$, $\mathcal{I} _ { \text{nd} } = \{ ( u _{j} )_{ j \in \mathbf{N}}$: there is a closed, nowhere-dense subset $\Gamma \subset \Omega$ such that for all $x \in \Omega \backslash \Gamma$ there are a $j _0$ and a neighbourhood $V \subset \Omega \backslash \Gamma$ of $x$ such that $u _ { j } | _ { V } \equiv 0$ for $j \geq j_0 \}$. This is the nowhere dense ideal introduced by E.E. Rosinger [a9] (cf. also Rosinger nowhere-dense generalized function algebra). The algebra $\mathcal{R} _ { \text{nd} } ( \Omega ) = \mathcal{B} / \mathcal{I} _ { \text{nd} }$ contains the algebra $C _ { \text{nd} } ^ { \infty } ( \Omega )$ of smooth functions defined off some nowhere-dense set as a subalgebra. Since 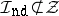 , the imbedding of $\mathcal{D} ^ { \prime } ( \Omega )$ cannot be done by convolution, but uses an algebraic basis.
, the imbedding of $\mathcal{D} ^ { \prime } ( \Omega )$ cannot be done by convolution, but uses an algebraic basis.
There are many variations on this theme, different sets $\Lambda$, different spaces $\mathcal{V}$. The algebras can be defined on smooth manifolds as well. Usually, further operations can be applied to the elements of these algebras: superposition with non-linear mappings, restriction to submanifolds, pointwise evaluation (with values in the corresponding ring of constants).
The algebras offer a general framework for studying all problems involving non-linear operations, differentiation, and distributional or otherwise non-smooth data and coefficients. Applications include non-linear partial differential equations, stochastic partial differential equations, Lie symmetry transformations, distributional metrics in general relativity, quantum field theory. For a survey of current applications, see [a4].
A second approach is based on the algebras constructed by V.K. Ivanov [a5] by means of analytic or harmonic regularization of homogeneous distributions and on the weak asymptotic expansions of V.P. Maslov (see e. g. [a7]). A simple, specific example is given by the space $h$ of distributions spanned by $\{ x ^ { i } , \text { vp } 1 / x ^ { j } , \delta ^ { ( k ) } ( x ) : i , j , k \in {\bf N} _ { 0 } \}$ in one dimension, where $ \operatorname{vp} ( . )$ denotes the principal value distribution and $\delta ^ { ( k ) } ( . )$ the $k$th derivative of the Dirac measure (cf. also Generalized function). Their harmonic regularizations generate a function algebra $h ^ { * }$ of smooth functions $f ^ { * } ( x , \varepsilon )$ defined on $( x , \varepsilon ) \in \mathbf{R} \times ( 0 , \infty )$. Each $f ^ { * } ( x , \varepsilon )$ has a unique weak asymptotic expansion of the form $\sum _ { j = m } ^ { \infty } f _ { j } ( x ) \varepsilon ^ { j }$ as $\varepsilon \rightarrow 0$ with coefficients $f _ { j } ( x )$ in the original space $h$; the summation starts at some, possibly negative, $m \in \bf Z$. The approach was extended [a2] to the class of associated homogeneous distributions. This way the structure of an algebra may be introduced on certain subspaces of the space of asymptotic series with distribution coefficients. As an application, asymptotic solutions to non-linear partial differential equations can be constructed by direct computation with the asymptotic series.
A relation with the previous construction of generalized function algebras is obtained by observing that harmonic regularization amounts to convolution with the kernel
\begin{equation*} \tau _ { \varepsilon } ( x ) = \frac { \varepsilon } { \pi } ( x ^ { 2 } + \varepsilon ^ { 2 } ) ^ { - 1 }. \end{equation*}
References
| [a1] | J.F. Colombeau, "New generalized functions and multiplication of distributions" , North-Holland (1984) MR0738781 Zbl 0532.46019 |
| [a2] | V.G. Danilov, V.P. Maslov, V.M. Shelkovich, "Algebras of singularities of singular solutions to first-order quasilinear strictly hyperbolic systems" Theoret. Math. Phys. , 114 : 1 (1998) pp. 3–55 MR1756560 |
| [a3] | Yu.V. Egorov, "A contribution to the theory of generalized functions" Russian Math. Surveys , 45 : 5 (1990) pp. 1–49 Zbl 0754.46034 |
| [a4] | "Nonlinear theory of generalized functions" M. Grosser (ed.) G. Hörmann (ed.) M. Kunzinger (ed.) M. Oberguggenberger (ed.) , Chapman and Hall/CRC (1999) MR1699842 Zbl 0918.00026 |
| [a5] | V.K. Ivanov, "An associative algebra of the simplest generalized functions" Sib. Math. J. , 20 (1980) pp. 509–516 |
| [a6] | H. König, "Multiplikation von Distributionen I" Math. Ann. , 128 (1955) pp. 420–452 MR0068745 Zbl 0064.11303 |
| [a7] | V.P. Maslov, G.A. Omel'yanov, "Asymptotic soliton-form solutions of equations with small dispersion" Russian Math. Surveys , 36 : 3 (1981) pp. 73–149 Zbl 0494.35080 |
| [a8] | A. Robinson, "Non-standard analysis" , North-Holland (1966) MR0205854 Zbl 0151.00803 |
| [a9] | E.E. Rosinger, "Nonlinear partial differential equations. Sequential and weak solutions" , North-Holland (1980) MR0590891 Zbl 0447.35001 |
| [a10] | C. Schmieden, D. Laugwitz, "Eine Erweiterung der Infinitesimalrechnung" Math. Z. , 69 (1958) pp. 1–39 MR0095906 Zbl 0082.04203 |
Generalized function algebras. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Generalized_function_algebras&oldid=56191